题目描述
给定一个由 0 和 1 组成的非空二维数组 grid ,用来表示海洋岛屿地图。 一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。 找到给定的二维数组中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
LCR 105. 岛屿的最大面积 - 力扣(LeetCode)
示例 :
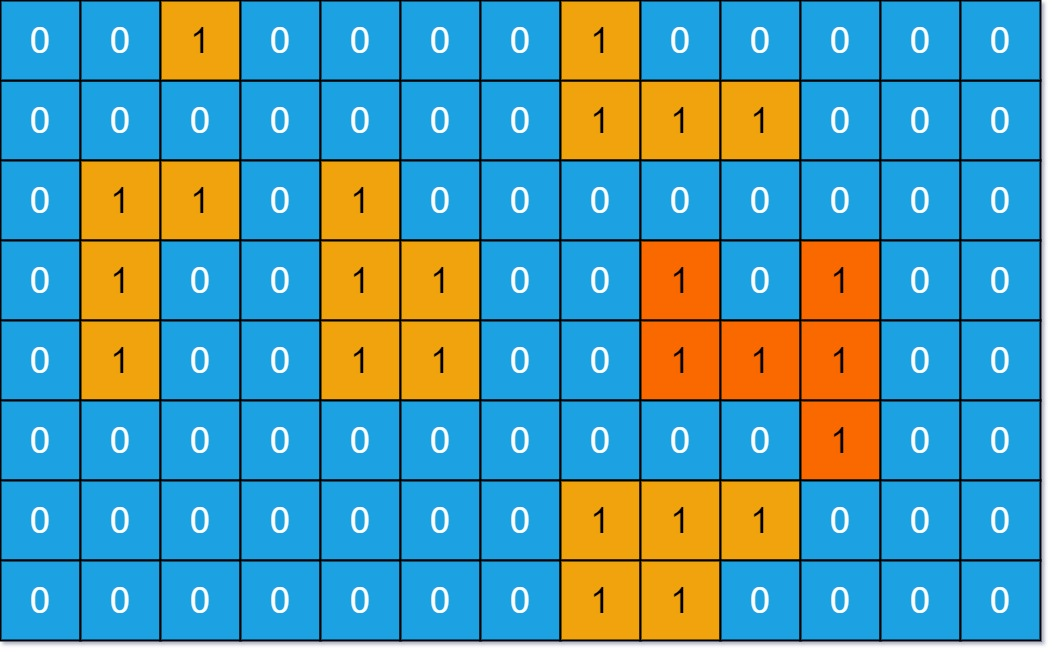
输入: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0], [0,1,0,0,1,1,0,0,1,1,1,0,0], [0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出: 6
解题思路
-
遍历整个网格:我们需要遍历二维数组中的每一个元素。
-
检查当前元素:对于每个元素,如果它是陆地(值为1),则意味着我们可能找到了一座岛屿的一部分。此时,我们需要启动一次DFS搜索来计算这座岛屿的面积。
-
DFS搜索:从当前陆地元素开始,递归地访问所有相邻的陆地元素,并将它们标记为已访问(例如,将它们的值从1更改为0或其他标记值)。在访问每个相邻元素时,我们增加岛屿面积的计数器。
-
记录最大面积:在每次DFS搜索结束时,我们得到了当前岛屿的面积。我们将这个面积与迄今为止找到的最大面积进行比较,并更新最大面积值(如果需要)。
-
继续遍历:我们继续遍历网格中的下一个元素,重复上述步骤,直到网格被完全遍历。
-
返回结果:最后,我们返回找到的最大岛屿面积。
DFS思路详解
-
递归基准条件:DFS的递归基准条件是当我们尝试访问一个不在网格范围内的元素、一个已经访问过的元素(即值为0或其他标记值),或者当我们达到网格的边界时。在这些情况下,我们停止递归。
-
递归步骤:对于当前陆地元素,我们首先将其标记为已访问,并增加岛屿面积的计数器。然后,我们对其上、下、左、右四个相邻元素进行递归调用DFS。但是,在调用之前,我们需要检查相邻元素是否在网格范围内内,并且它们是否是陆地(值为1)。
class Solution {
public:
int n, m;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int maxAreaOfIsland(vector<vector<int>>& grid) {
n = grid.size();
m = grid[0].size();
int ret = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) {
int area = 0;
dfs(grid, i, j, &area);
ret = max(ret, area);
}
}
}
return ret;
}
void dfs(vector<vector<int>>& grid, int i, int j, int* parea) {
grid[i][j] = 2;
(*parea)++;
for (int k = 0; k < 4; k++) {
int tmpx = i + dx[k];
int tmpy = j + dy[k];
if (tmpx >= 0 && tmpx < n && tmpy >= 0 && tmpy < m &&
grid[tmpx][tmpy] == 1) {
dfs(grid, tmpx, tmpy, parea);
}
}
}
};