一、二叉树中的伪回文路径
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。
请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。
示例 1:
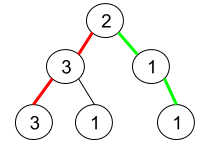
输入:root = [2,3,1,3,1,null,1]
输出:2
解释:上图为给定的二叉树。总共有 3 条从根到叶子的路径:红色路径 [2,3,3] ,绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中,只有红色和绿色的路径是伪回文路径,因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ,绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
思路:
要找到伪回文路径,根据特征来看:伪回文路径中数量为奇数的数的个数:要么有一个、要么没有
所以我们就统计每一个字串中数的数量,然后遍历判断其中数量为奇数的个数,>1就不是伪回文串了。
代码:
class Solution {
public int pseudoPalindromicPaths (TreeNode root) {
int[] arr=new int[10];
return dfs(root,arr);
}
public int dfs(TreeNode root,int[] arr){
if(root==null)return 0;
int res=0;
arr[root.val]^=1;
if(root.left==null&&root.right==null){
res=count(arr);
}else{
res=dfs(root.left,arr)+dfs(root.right,arr);
}
arr[root.val]^=1;
return res;
}
public int count(int[] arr){
int res=0;
for(int num:arr){
res+=num;
}
return res<=1?1:0;
}
}二、祖父节点值为偶数的节点和
你一棵二叉树,请你返回满足以下条件的所有节点的值之和:
该节点的祖父节点的值为偶数。(一个节点的祖父节点是指该节点的父节点的父节点。)
如果不存在祖父节点值为偶数的节点,那么返回 0 。
思路:
整体递归,将祖父节点、父节点、子节点看作一个整体,往下去递归。当遇到符合条件的整体就将子节点的值添加。
条件:
if(grandParent!=null&&grandParent.val%2==0)代码:
class Solution {
public int sumEvenGrandparent(TreeNode root) {
return dfs(null,null,root);
}
public int dfs(TreeNode grandparent,TreeNode parent,TreeNode root){
if(root==null)return 0;
int add=0;
if(grandparent!=null&&grandparent.val%2==0){
add=root.val;
}
return add+dfs(parent,root,root.left)+dfs(parent,root,root.right);
}
}三、节点与其祖先之间的最大差值
给定二叉树的根节点 root,找出存在于 不同 节点 A 和 B 之间的最大值 V,其中 V = |A.val - B.val|,且 A 是 B 的祖先。
(如果 A 的任何子节点之一为 B,或者 A 的任何子节点是 B 的祖先,那么我们认为 A 是 B 的祖先)
 最大差值就是:7
最大差值就是:7
思路:
在遍历的时候,我们需要维护一个最大值和最小值。然后将每次的值和最大/小值比较即可。
eg:
第一层的时候 最大值、最小值都是8,最大差值为0
第二层 左子树 最大值、最小值分别为8、3,最大差值为5;
第二层 右子树 最大值、最小值分别为10、8,最大差值为2;
以此类推...
代码:
class Solution {
public int maxAncestorDiff(TreeNode root) {
return dfs(root,root.val,root.val,0);
}
public int dfs(TreeNode root,int min,int max,int maxDiff){
if(root==null)return 0;
min=Math.min(min,root.val);
max=Math.max(max,root.val);
maxDiff=Math.max(maxDiff,Math.max(root.val-min,max-root.val));
int leftDiff=dfs(root.left,min,max,maxDiff);
int rightDiff=dfs(root.right,min,max,maxDiff);
return Math.max(maxDiff,Math.max(leftDiff,rightDiff));
}
}