算法原理
堆排序是一种基于比较的排序算法,它利用了数据结构中的堆(Heap)。堆是一种特殊的完全二叉树,分为最大堆(Max-Heap)和最小堆(Min-Heap)。在最大堆中,每个父节点的值都大于或等于其子节点的值;在最小堆中,每个父节点的值都小于或等于其子节点的值。
构建最大堆:将给定的无序数组重新调整成一个最大堆。最大堆是堆排序的核心数据结构,它确保了堆顶元素(根节点)是当前堆中的最大值。
排序:
- 将最大堆的根节点(即当前堆中最大值)与堆的最后一个元素交换位置。此时,最大值被移动到数组的末尾,并从堆中移除。
- 对新的堆顶元素进行堆调整。调整后的堆可能会破坏最大堆的性质,因此需要重新调整堆以恢复最大堆的性质。
- 重复上述步骤,将堆顶元素移到已排序部分的末尾,直到堆的大小为 1。最终,所有元素将按从小到大的顺序排列。
完成排序:经过上述步骤后,数组中的元素将按照从小到大的顺序排列。
堆排序算法由 J.W.J. Williams 在 1964 年首次提出。他在论文中描述了这一算法的基本概念,并将其称为“堆排序”算法。堆排序的核心思想是通过最大堆的性质来完成排序,这一思想是基于完全二叉树的特性。
堆排序的发明背景与计算机科学早期的发展密切相关。在计算机科学发展的初期,排序算法是一个重要的研究领域。随着计算机应用的普及,如何高效地对大量数据进行排序成为一个实际问题。J.W.J. Williams 的研究为解决这一问题提供了一种新的思路。
堆排序不仅具有良好的时间复杂度(O(n log n)),而且在实际应用中也表现出稳定的性能。这使得堆排序成为计算机科学中一个经典且重要的排序算法。
实例分析
假设我们有一个无序数组 [4, 10, 3, 5, 1],通过堆排序将其排序为 [1, 3, 4, 5, 10]。
初始数组:[4, 10, 3, 5, 1]
构建最大堆:将 10 放到根节点,堆结构如下:
10
/ \
5 3
/ \
4 1
- 对堆进行调整后,数组变为
[10, 5, 3, 4, 1]
交换堆顶与末尾元素:交换 10 和 1,得到 [1, 5, 3, 4, 10]。此时最大元素 10 已排好序。
调整剩余部分:
- 调整堆结构,得到 `[5, 4, 3, 1, 10]`。
- 再次交换堆顶和末尾,得到 `[1, 4, 3, 5, 10]`。
- 重复上述过程,最终得到 `[1, 3, 4, 5, 10]`。
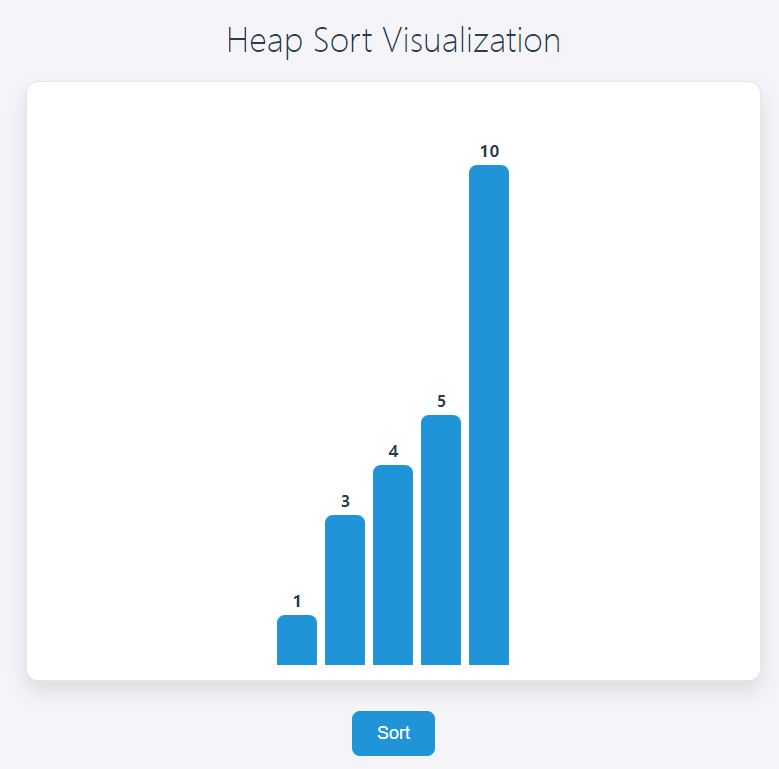
动态实现
下面是一个简单的示例,演示如何使用 JavaScript 实现堆排序,并通过 HTML 来展示排序的过程。
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>Heap Sort Visualization</title>
<style>
body {
font-family: 'Roboto', sans-serif;
background-color: #f4f4f9;
display: flex;
flex-direction: column;
align-items: center;
justify-content: center;
height: 100vh;
margin: 0;
padding: 0;
}
h1 {
color: #2c3e50;
margin-bottom: 20px;
font-weight: 300;
font-size: 2em;
text-align: center;
}
.array-container {
display: flex;
justify-content: center;
align-items: flex-end;
width: 90%;
max-width: 1000px;
height: 600px;
border: 1px solid #e1e8eb;
border-radius: 12px;
background-color: #ffffff;
box-shadow: 0 10px 20px rgba(0, 0, 0, 0.1);
padding: 15px;
box-sizing: border-box;
overflow: hidden;
}
.array-bar {
width: 40px;
margin: 0 4px;
background-color: #3498db;
border-radius: 8px 8px 0 0;
transition: all 0.6s ease;
position: relative;
}
.array-bar::after {
content: attr(data-value);
position: absolute;
top: -25px;
left: 50%;
transform: translateX(-50%);
font-size: 16px;
color: #2c3e50;
font-weight: bold;
}
button {
padding: 12px 25px;
margin-top: 30px;
font-size: 18px;
color: #ffffff;
background-color: #3498db;
border: none;
border-radius: 8px;
cursor: pointer;
transition: background-color 0.4s ease, transform 0.2s ease;
}
button:hover {
background-color: #2980b9;
}
button:active {
background-color: #1c648d;
transform: scale(0.98);
}
</style>
</head>
<body>
<h1>Heap Sort Visualization</h1>
<div class="array-container" id="array-container"></div>
<button onclick="heapSort()">Sort</button>
<script>
const array = [4, 10, 3, 5, 1];
function displayArray(arr) {
const container = document.getElementById('array-container');
container.innerHTML = '';
arr.forEach(value => {
const bar = document.createElement('div');
bar.style.height = `${value * 50}px`;
bar.classList.add('array-bar');
bar.setAttribute('data-value', value); // 显示条形图的数值
container.appendChild(bar);
});
}
function heapify(arr, length, i) {
let largest = i;
let left = 2 * i + 1;
let right = 2 * i + 2;
if (left < length && arr[left] > arr[largest]) {
largest = left;
}
if (right < length && arr[right] > arr[largest]) {
largest = right;
}
if (largest !== i) {
[arr[i], arr[largest]] = [arr[largest], arr[i]];
heapify(arr, length, largest);
}
}
async function heapSort() {
let length = array.length;
for (let i = Math.floor(length / 2 - 1); i >= 0; i--) {
heapify(array, length, i);
}
for (let i = length - 1; i >= 0; i--) {
[array[0], array[i]] = [array[i], array[0]];
heapify(array, i, 0);
displayArray(array);
await new Promise(resolve => setTimeout(resolve, 500)); // 动态显示
}
}
// Initial display
displayArray(array);
</script>
</body>
</html>
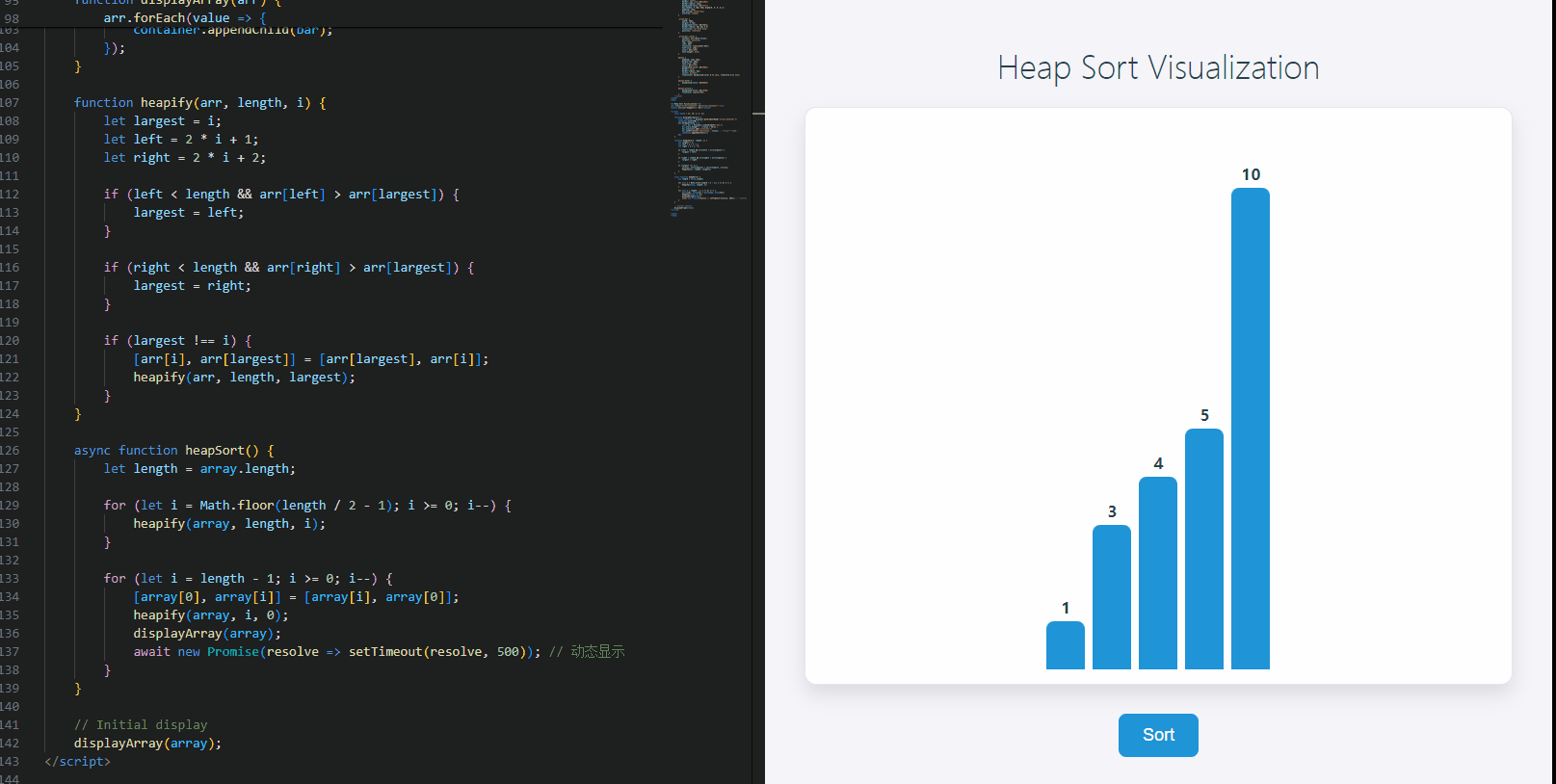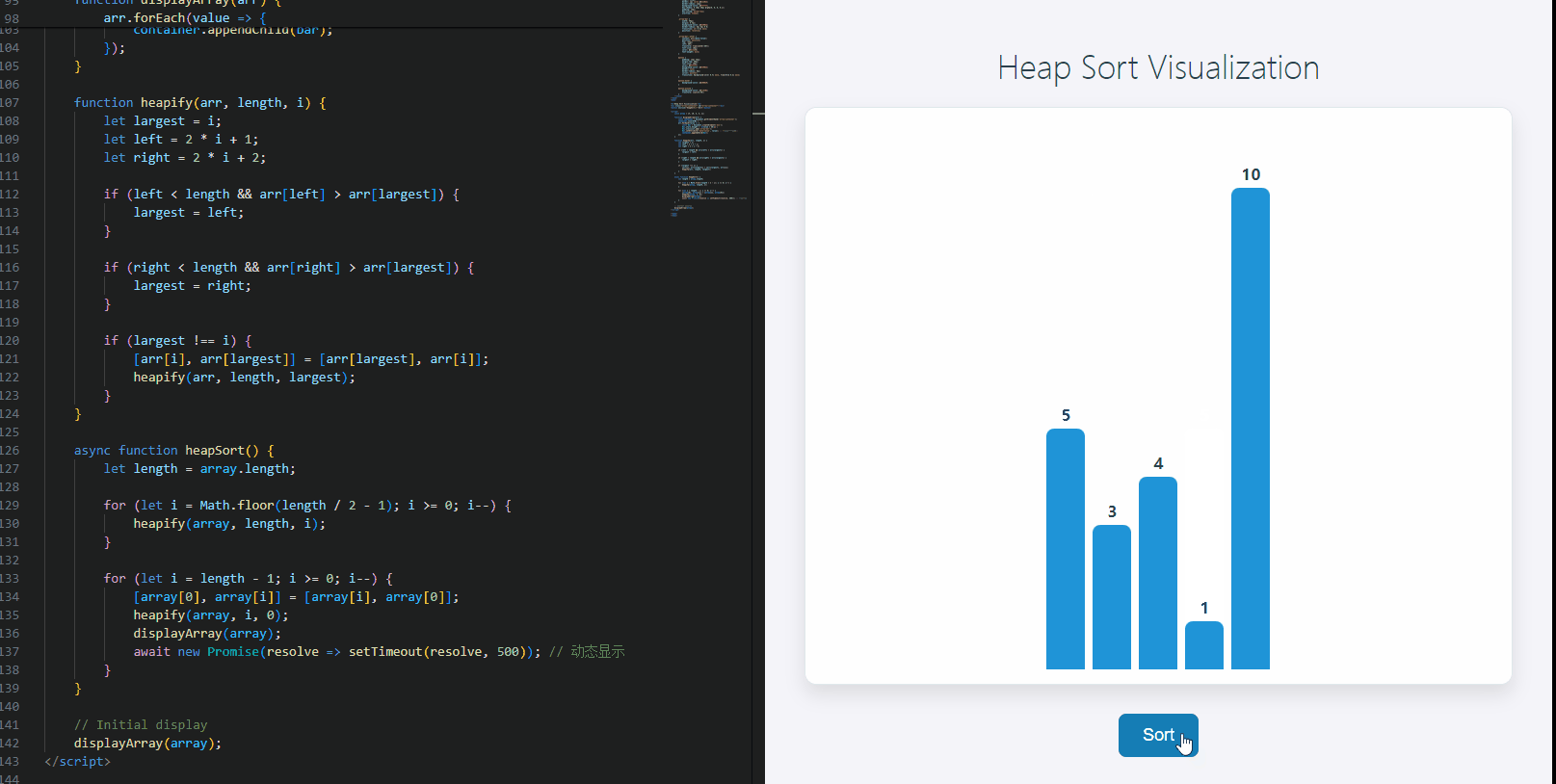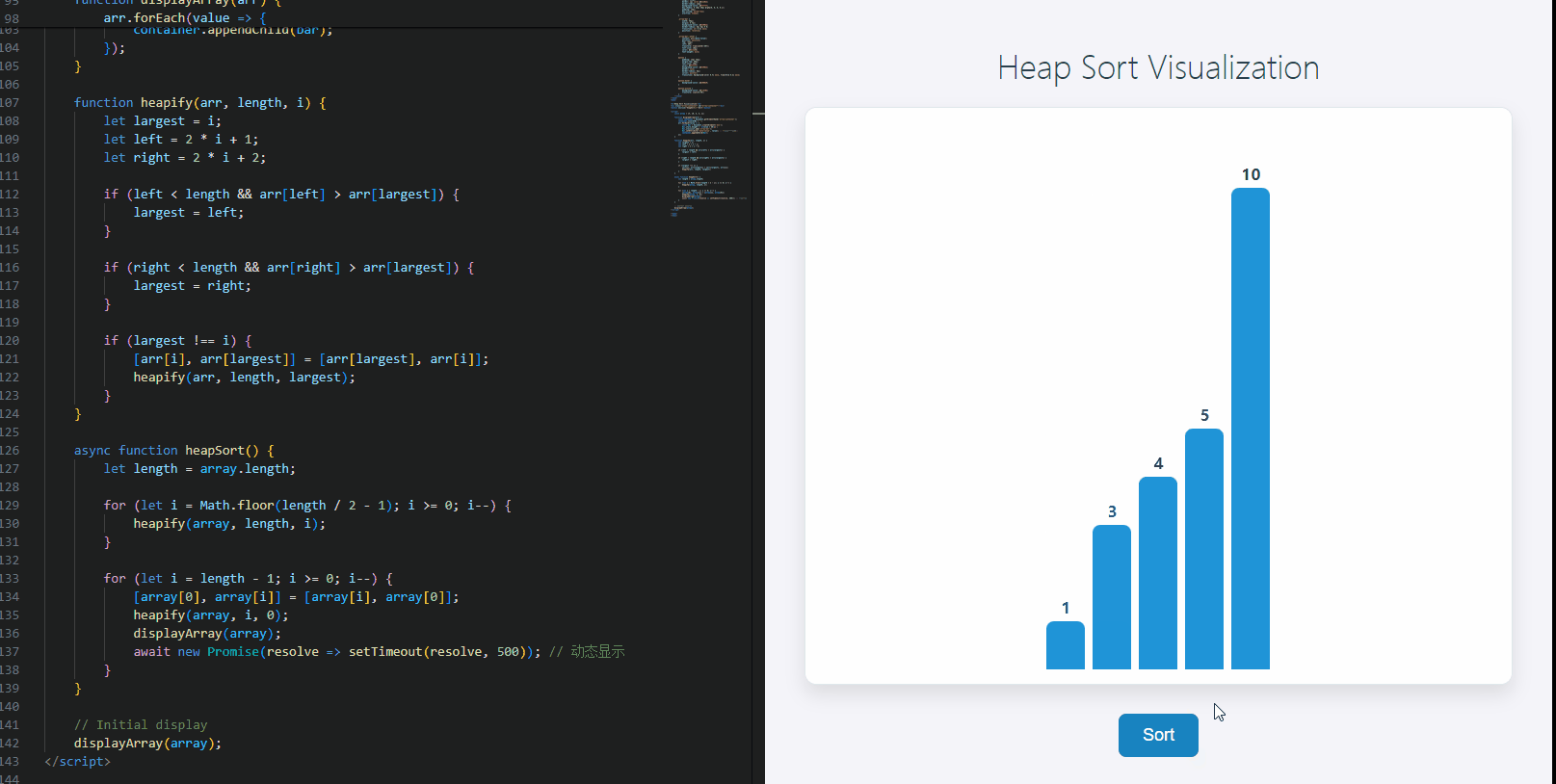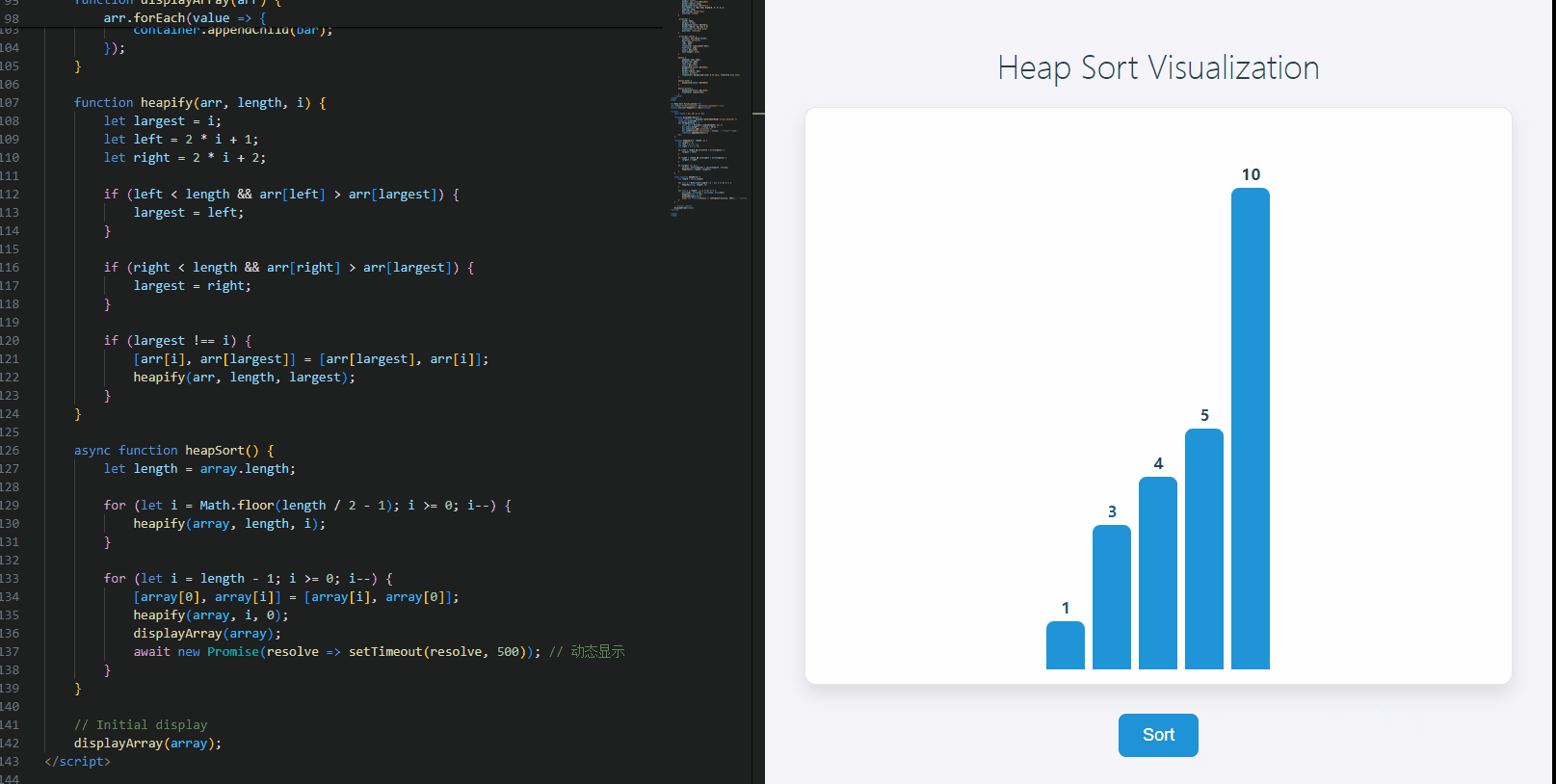
代码解释
在下面的代码中,我们实现了堆排序算法,并动态展示了排序过程。
const array = [4, 10, 3, 5, 1];
function displayArray(arr) {
const container = document.getElementById('array-container');
container.innerHTML = '';
arr.forEach(value => {
const bar = document.createElement('div');
bar.style.height = `${value * 50}px`; // 设置条形图的高度
bar.classList.add('array-bar');
bar.setAttribute('data-value', value); // 显示条形图的数值
container.appendChild(bar);
});
}
1. displayArray 函数:
- 目的:动态显示数组的当前状态。
- 参数:
arr是需要显示的数组。 - 操作:
- 清空数组容器 (
container.innerHTML = '')。 - 遍历数组,创建每个元素的条形图 (
div)。 - 设置条形图的高度来表示数组元素的值 (
bar.style.height =${value * 50}px`),更高的条形图表示更大的值。 - 将条形图添加到容器中 (
container.appendChild(bar))。
- 清空数组容器 (
function heapify(arr, length, i) {
let largest = i;
let left = 2 * i + 1;
let right = 2 * i + 2;
if (left < length && arr[left] > arr[largest]) {
largest = left;
}
if (right < length && arr[right] > arr[largest]) {
largest = right;
}
if (largest !== i) {
[arr[i], arr[largest]] = [arr[largest], arr[i]];
heapify(arr, length, largest);
}
}
2. heapify 函数:
- 目的:将数组调整成一个最大堆,以便在堆排序中能够正确地取出最大值。
- 参数:
arr:待调整的数组。length:当前堆的有效大小。i:当前节点的索引。
- 操作:
- 初始化:假设当前节点是最大的节点 (
largest = i)。 - 比较左子节点:如果左子节点存在且大于当前节点,则更新最大节点为左子节点 (
largest = left)。 - 比较右子节点:如果右子节点存在且大于当前节点,则更新最大节点为右子节点 (
largest = right)。 - 交换:如果最大节点不是当前节点,则交换它们,并递归调用
heapify以确保堆的性质在交换后仍然保持。
- 初始化:假设当前节点是最大的节点 (
async function heapSort() {
let length = array.length;
// 建立最大堆
for (let i = Math.floor(length / 2 - 1); i >= 0; i--) {
heapify(array, length, i);
}
// 排序
for (let i = length - 1; i >= 0; i--) {
[array[0], array[i]] = [array[i], array[0]]; // 交换当前根节点与最后一个节点
heapify(array, i, 0); // 重新调整堆
displayArray(array); // 更新显示
await new Promise(resolve => setTimeout(resolve, 500)); // 等待一段时间,以便用户看到排序过程
}
}
// 初次显示数组
displayArray(array);
3. heapSort 函数:
- 目的:执行堆排序算法,并动态展示排序过程。
- 操作:
- 建立最大堆:从最后一个非叶子节点开始,向上调整堆,确保整个数组满足最大堆的性质。
- 排序过程:
- 交换根节点(最大值)与当前堆的最后一个节点,并减少堆的有效大小 (
i)。 - 重新调整堆以确保堆的性质,并更新显示。
- 使用
await new Promise(resolve => setTimeout(resolve, 500))添加延迟,便于用户观察排序过程。
- 交换根节点(最大值)与当前堆的最后一个节点,并减少堆的有效大小 (



![[AutoSar]BSW_Diagnostic_005 RoutineControl service (0x31)介绍](https://i-blog.csdnimg.cn/direct/3e846ae973f64a61844f4ce815e86fa0.png)