目录
3.1 非线性规划概述
3.2 约束优化问题
3.3 无约束优化问题的Matlab求解
3.4 牛顿法与梯度下降法
Matlab代码示例:梯度下降法求解简单非线性问题
3.5 非线性规划在机器学习中的应用
习题 3
总结
非线性规划(Nonlinear Programming, NLP)是数学规划中更加复杂的一类问题,与线性规划和整数规划不同,非线性规划的目标函数或约束条件中包含非线性项。非线性规划广泛应用于工程设计、经济管理、机器学习等领域,其求解难度和复杂性远远超过线性规划。本章将介绍非线性规划的基本概念、非线性规划模型的构建、常见的求解方法以及相关的应用实例。
3.1 非线性规划概述
非线性规划问题可以形式化为目标函数和约束条件中的某些部分是非线性关系的优化问题。通常表示为:
-
目标函数:最大化或最小化一个非线性函数。
-
约束条件:可能包括线性或非线性的不等式与等式。
例如,优化一个包含平方项或指数项的目标函数的问题就属于非线性规划。这类问题在工程设计、经济模型中较为常见,例如设计一个能够承受最大压力的构件,或者最大化产品的收益并考虑市场影响的非线性模型。
| 类型 | 描述 | 应用场景 |
|---|---|---|
| 非线性目标 | 目标函数包含非线性项 | 工程设计、经济模型 |
| 非线性约束 | 约束条件包含非线性关系 | 机器学习、数据拟合 |
3.2 约束优化问题
在非线性规划中,约束条件可以分为等式约束和不等式约束。约束优化问题通常需要考虑多个条件,并且这些条件可能是非线性关系。例如,设计一个机械部件的形状,使其体积最小化,但需要满足强度和形变的约束。
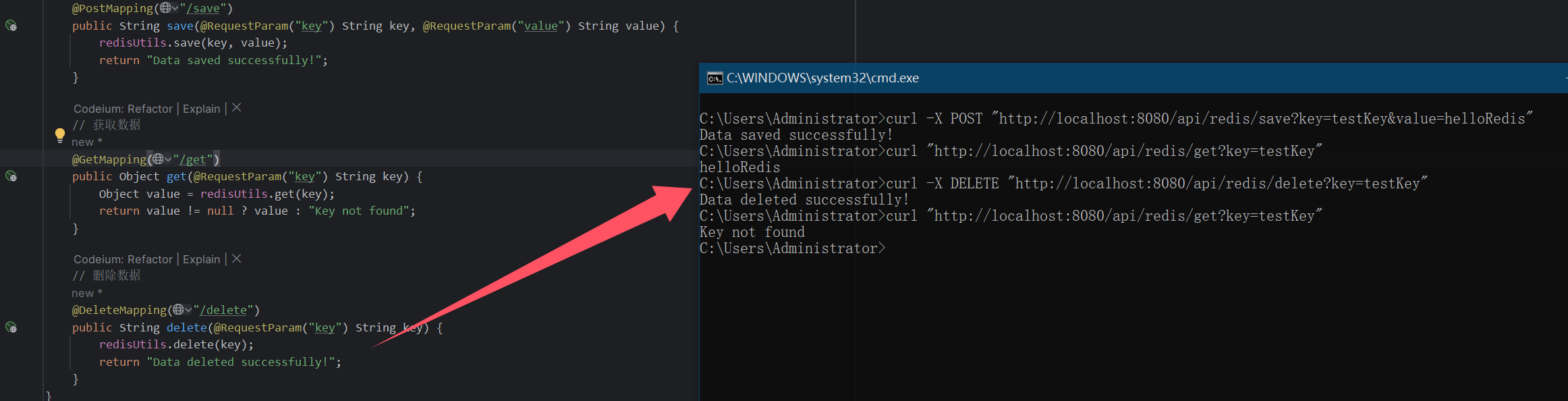
求解非线性规划的关键在于找到满足所有约束条件的最优解。Matlab中有多种工具可以用于解决此类问题,其中最常用的是fmincon函数。
Matlab代码示例:
% 定义目标函数
obj_fun = @(x) x(1)^2 + x(2)^2 + 3*x(3)^2; % 目标函数:x1^2 + x2^2 + 3*x3^2
% 定义不等式约束条件
A = [1, 2, 3];
b = 10; % 约束条件:x1 + 2*x2 + 3*x3 <= 10
% 定义等式约束条件
Aeq = [1, 1, 1];
beq = 5; % 约束条件:x1 + x2 + x3 = 5
% 定义变量的边界
lb = [0; 0; 0]; % 变量下界
ub = [inf; inf; inf]; % 变量上界
% 初始猜测值
x0 = [1; 1; 1];
% 使用fmincon函数求解非线性规划问题
options = optimoptions('fmincon', 'Display', 'iter');
[x, fval] = fmincon(obj_fun, x0, A, b, Aeq, beq, lb, ub, [], options);
% 输出结果
fprintf('最优解:x1 = %.2f, x2 = %.2f, x3 = %.2f\n', x(1), x(2), x(3));
fprintf('最小化目标函数值:%.2f\n', fval);上述代码通过定义一个简单的目标函数,以及若干约束条件,使用fmincon函数进行求解。该例子展示了如何构建非线性目标函数以及不同类型的约束条件。
3.3 无约束优化问题的Matlab求解
无约束优化问题是一类没有任何约束条件的非线性规划问题,其目标是在整个定义域内找到最优解。这种情况下,求解过程相对简单,只需要考虑目标函数的最小化或最大化。
Matlab中,fminunc函数可用于求解无约束的非线性优化问题。
Matlab代码示例:
% 定义目标函数
obj_fun = @(x) (x(1) - 3)^2 + (x(2) + 5)^2; % 目标函数:(x1 - 3)^2 + (x2 + 5)^2
% 初始猜测值
x0 = [0; 0];
% 使用fminunc函数求解无约束优化问题
options = optimoptions('fminunc', 'Algorithm', 'quasi-newton', 'Display', 'iter');
[x, fval] = fminunc(obj_fun, x0, options);
% 输出结果
fprintf('最优解:x1 = %.2f, x2 = %.2f\n', x(1), x(2));
fprintf('最小化目标函数值:%.2f\n', fval);在这个代码中,我们定义了一个简单的二元函数,通过fminunc求解得到了使该函数最小的点。fminunc采用准牛顿法等多种算法,可以有效解决无约束的优化问题。
3.4 牛顿法与梯度下降法
非线性规划中,求解算法的选择至关重要,其中牛顿法和梯度下降法是两种常用的求解方法。
-
牛顿法:利用目标函数的二阶导数信息,通过迭代求解目标函数的最优点。牛顿法收敛速度快,但计算二阶导数的代价较高。
-
梯度下降法:使用目标函数的一阶导数信息,沿负梯度方向不断迭代,以逐步找到目标函数的最小值。梯度下降法计算简单,但可能陷入局部最优解。
| 方法 | 优势 | 劣势 |
| 牛顿法 | 收敛速度快,精度高 | 计算二阶导数代价高 |
| 梯度下降法 | 实现简单,计算成本低 | 容易陷入局部最优解 |
Matlab代码示例:梯度下降法求解简单非线性问题
% 定义目标函数
obj_fun = @(x) (x(1) - 3)^2 + (x(2) - 2)^2; % 目标函数
% 梯度函数
grad_fun = @(x) [2 * (x(1) - 3); 2 * (x(2) - 2)];
% 初始猜测值
x = [0; 0];
alpha = 0.1; % 学习率
max_iter = 100;
% 梯度下降迭代
for i = 1:max_iter
grad = grad_fun(x);
x = x - alpha * grad;
fprintf('第%d次迭代:x1 = %.2f, x2 = %.2f, 目标函数值 = %.2f\n', i, x(1), x(2), obj_fun(x));
if norm(grad) < 1e-6
break;
end
end
% 输出最优解
fprintf('最优解:x1 = %.2f, x2 = %.2f\n', x(1), x(2));以上代码演示了使用梯度下降法求解一个简单非线性优化问题的过程。通过不断迭代更新变量,我们最终找到了目标函数的最小值点。
3.5 非线性规划在机器学习中的应用
非线性规划在机器学习中的应用十分广泛,尤其是在模型训练和参数优化中。例如,支持向量机(SVM)模型的训练涉及到非线性约束优化问题,神经网络的训练过程中也涉及到通过优化损失函数来调整网络权重的过程。
在机器学习中,非线性规划用于:
-
损失函数最小化:在训练过程中最小化误差。
-
参数正则化:通过正则化项来控制模型复杂度。
-
超参数优化:寻找最优的模型参数组合,以提高模型的性能。
通过非线性规划,可以有效地调整模型参数,从而获得更好的泛化性能。
习题 3
在第三章结束后,提供了一些相关的习题,帮助读者深入理解非线性规划的建模和求解方法。习题3包括:
-
机械设计优化问题:设计一个机械部件,使其重量最小化,但需要满足强度和形变的约束条件。
-
无约束优化问题:求解目标函数
f(x, y) = (x - 4)^2 + (y + 3)^2的最小值,并使用Matlab编写代码求解。 -
机器学习模型优化:针对一个简单的线性回归模型,定义损失函数并使用梯度下降法进行训练,以找到最优的模型参数。
通过这些习题,读者可以进一步掌握非线性规划在实际中的应用,以及如何利用Matlab和其他工具进行求解。
总结
第三章介绍了非线性规划的基本概念及其求解方法,包括无约束优化、约束优化、梯度下降法和牛顿法等。非线性规划在许多复杂的实际应用中有着重要作用,尤其是在工程设计和机器学习等领域。尽管非线性规划的求解复杂度较高,但通过合适的求解方法和优化策略,可以有效地找到最优解。接下来的章节将进一步探索其他优化问题,如动态规划和多目标优化等,帮助读者更全面地理解优化理论和实践。