参考文献链接：代码随想录

本人代码是Java版本的，如有别的版本需要请上代码随想录网站查看。

第77题. 组合

力扣题目链接

解题思路

这道题目乍一看可以用暴力解法解决，但如果k的数量增加那就需要套特别多的循环，所以这种组合类题目要学回溯算法。

对于这道题来说，例如1到4内，找两位数组合，也就是12，13，14，23，24，34.

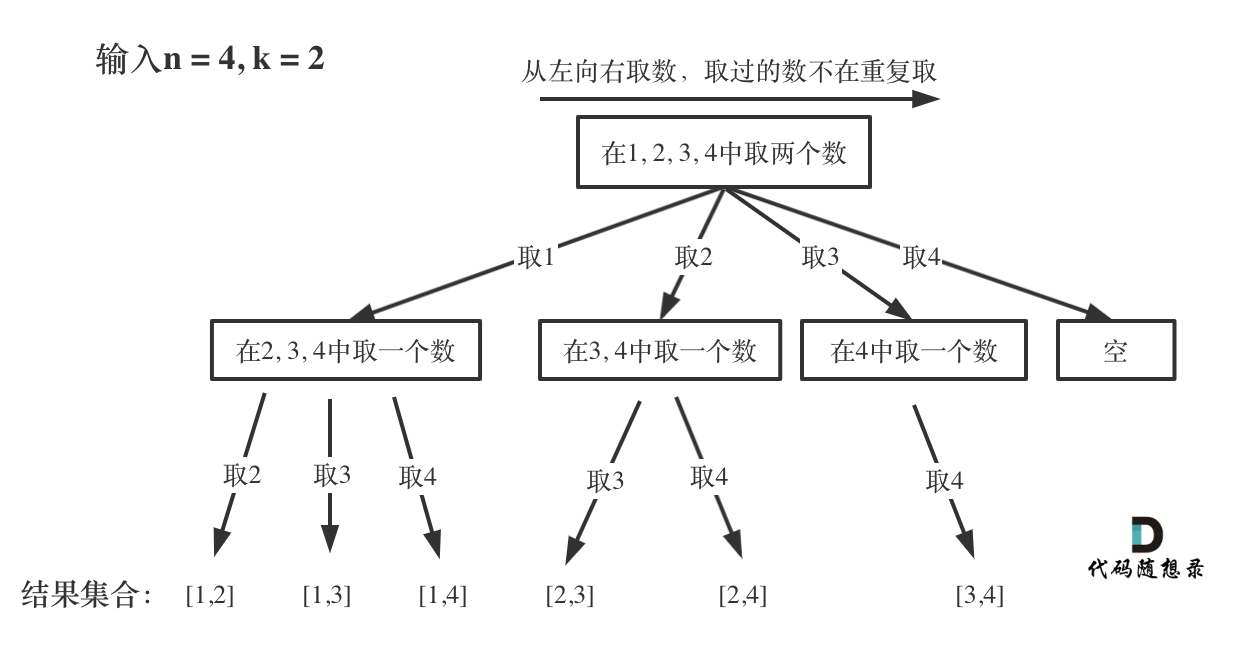
回溯算法都可以化成一个n叉树，其实类似之前二叉树的递归其中还包含一些回溯。更多思路我们在代码中体现。

代码示例

class Solution {
    //用于存一个组合和最后的结果
    private List<Integer> paths = new ArrayList<>();
    private List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return result;
    }
    //回溯本质还是递归，第一步确定参数，startIndex就是起始，比如说我们第一次递归从1开始，第二次就从2，这样12，13，14才行。
    public void backtracking(int n,int k,int startIndex){
        //如果paths种长度为k，说明收集到一个集合，就要保存一下
        if(paths.size() == k){
            result.add(new ArrayList<>(paths));
            return;
        }
        //for循环遍历
        for(int i = startIndex;i <= n;i++){
            //先把第一个元素加入
            paths.add(i);
            //递归，这次递归从i+1开始，就可以收集到paths了
            backtracking(n,k,i + 1);
            //remove掉刚才加入的就是回溯，这是为了更多的组合，如果不删除的话paths永远都是那两个数字。
            paths.remove(paths.size() - 1);
        }
    } 
}

剪枝操作

我们回溯算法也是一种暴力解法，所以我们可以看一下如何剪枝。

一般回溯的剪枝操作都是对for循环的条件入手，比如这道题，假如n=5 k=4，如果此时paths从3开始收集，345也不会收集到k个元素了，所以这种要剪枝。

我们path中的大小是path.size(),还需要加入k-path.size()个元素，一共有n个，并且起步是从n = 1开始的，所以i <= n - (k-path.size()) + 1即可。

for(int i = startIndex;i <= i <= n - (k-path.size()) + 1;i++)

216.组合总和III

力扣题目链接

解题思路

这道题目跟上一题一样，回溯过程都相同，只不过逻辑处理改一下即可。剪枝操作注意一下。

代码示例

class Solution {
    private List<Integer> paths = new ArrayList<>();
    private List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(k,n,1,0);
        return result;
    }

    public void backtracking(int k,int n,int startIndex,int sum){
        //做剪枝
        if(sum > n){
            return;
        }
        if(paths.size() == k){
            if(sum == n){
                result.add(new ArrayList<>(paths));
            }
            return;
        }
        for(int i = startIndex;i <= 9 - (k - paths.size()) + 1;i++){
            paths.add(i);
            backtracking(k,n,i+1,sum + i);
            paths.remove(paths.size() - 1);
        }
    }
}

17.电话号码的字母组合

力扣题目链接

解题思路

这道题跟上面的题有些不同，上面的递归函数有startIndex，因为我们需要控制从哪里开始，但这道题我们是不同的字符串，只需要判断这次递归的是哪个字符串即可。

把该字符串某个字符加入后就下一次递归去加入别的字符串的字符，通过index+1控制不同的字符串即可。

代码示例

class Solution {
    private List<String> result = new ArrayList<>();
    private StringBuilder sb = new StringBuilder();
    //映射关系
    private String[] strings = new String[]{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};

    public List<String> letterCombinations(String digits) {
        if(digits.length() == 0){
            return result;
        }
        backtracing(digits,0);
        return result;
    }
	
    public void backtracing(String digits,int index){
        //终止条件
        if(index == digits.length()){
            result.add(new String(sb));
            return;
        }
        //首先先获取本次递归对应的字符串
        String temp = strings[digits.charAt(index) - '0'];
        //循环这个字符串
        for(int i = 0;i < temp.length();i++){
            //把该字符串某个字符加入后就下一次递归去加入别的字符串的字符
            sb.append(temp.charAt(i));
            backtracing(digits,index + 1);
            //回溯
            sb.deleteCharAt(sb.length()-1);
        }
    }
}