ORB-SLAM2 ---- Tracking::CreateInitialMapMonocular函数

news2024/9/21 3:19:05

目录

1.函数作用

2.函数解析

2.1 调用函数解析

2.2  Tracking::CreateInitialMapMonocular函数总体思路

2.2.1 代码

2.2.2 总体思路解析 

2.3 MapPoint::ComputeDistinctiveDescriptors函数解析

2.3.1 函数作用

2.3.2 代码 

2.3.3 函数解析 

2.4 MapPoint::UpdateNormalAndDepth函数解析 

2.4.1 函数作用

2.4.2 代码 

2.4.3 函数解析  

1.函数作用

        单目相机成功初始化后用三角化得到的点生成MapPoints

2.函数解析

2.1 调用函数解析

        单目地图初始化Tracking::MonocularInitialization函数中调用本函数，这是初始化单目SLAM的最后一步，我们在之前已经完成了单目初始化器的创建、匹配了两帧的特征点、恢复了两帧的运动位姿、用三角化生成了地图点，接下来我们要调用此函数利用生成的3D点实现生成地图点。

2.2  Tracking::CreateInitialMapMonocular函数总体思路

2.2.1 代码

/**
 * @brief 单目相机成功初始化后用三角化得到的点生成MapPoints
 * 
 */
void Tracking::CreateInitialMapMonocular()
{
    // Create KeyFrames 认为单目初始化时候的参考帧和当前帧都是关键帧
    KeyFrame* pKFini = new KeyFrame(mInitialFrame,mpMap,mpKeyFrameDB);  // 第一帧
    KeyFrame* pKFcur = new KeyFrame(mCurrentFrame,mpMap,mpKeyFrameDB);  // 第二帧

    // Step 1 将初始关键帧,当前关键帧的描述子转为BoW
    pKFini->ComputeBoW();
    pKFcur->ComputeBoW();

    // Insert KFs in the map
    // Step 2 将关键帧插入到地图
    mpMap->AddKeyFrame(pKFini);
    mpMap->AddKeyFrame(pKFcur);

    // Create MapPoints and asscoiate to keyframes
    // Step 3 用初始化得到的3D点来生成地图点MapPoints
    //  mvIniMatches[i] 表示初始化两帧特征点匹配关系。
    //  具体解释：i表示帧1中关键点的索引值，vMatches12[i]的值为帧2的关键点索引值,没有匹配关系的话，vMatches12[i]值为 -1
    for(size_t i=0; i<mvIniMatches.size();i++)
    {
        // 没有匹配，跳过
        if(mvIniMatches[i]<0)
            continue;

        //Create MapPoint.
        // 用三角化点初始化为空间点的世界坐标
        cv::Mat worldPos(mvIniP3D[i]);

        // Step 3.1 用3D点构造MapPoint
        MapPoint* pMP = new MapPoint(
            worldPos,
            pKFcur, 
            mpMap);

        // Step 3.2 为该MapPoint添加属性：
        // a.观测到该MapPoint的关键帧
        // b.该MapPoint的描述子
        // c.该MapPoint的平均观测方向和深度范围

        // 表示该KeyFrame的2D特征点和对应的3D地图点
        pKFini->AddMapPoint(pMP,i);
        pKFcur->AddMapPoint(pMP,mvIniMatches[i]);

        // a.表示该MapPoint可以被哪个KeyFrame的哪个特征点观测到
        pMP->AddObservation(pKFini,i);
        pMP->AddObservation(pKFcur,mvIniMatches[i]);

        // b.从众多观测到该MapPoint的特征点中挑选最有代表性的描述子
        pMP->ComputeDistinctiveDescriptors();
        // c.更新该MapPoint平均观测方向以及观测距离的范围
        pMP->UpdateNormalAndDepth();

        //Fill Current Frame structure
        //mvIniMatches下标i表示在初始化参考帧中的特征点的序号
        //mvIniMatches[i]是初始化当前帧中的特征点的序号
        mCurrentFrame.mvpMapPoints[mvIniMatches[i]] = pMP;
        mCurrentFrame.mvbOutlier[mvIniMatches[i]] = false;

        //Add to Map
        mpMap->AddMapPoint(pMP);
    }

    // Update Connections
    // Step 3.3 更新关键帧间的连接关系
    // 在3D点和关键帧之间建立边，每个边有一个权重，边的权重是该关键帧与当前帧公共3D点的个数
    pKFini->UpdateConnections();
    pKFcur->UpdateConnections();

    // Bundle Adjustment
    cout << "New Map created with " << mpMap->MapPointsInMap() << " points" << endl;

    // Step 4 全局BA优化，同时优化所有位姿和三维点
    Optimizer::GlobalBundleAdjustemnt(mpMap,20);

    // Set median depth to 1
    // Step 5 取场景的中值深度，用于尺度归一化 
    // 为什么是 pKFini 而不是 pKCur ? 答：都可以的，内部做了位姿变换了
    float medianDepth = pKFini->ComputeSceneMedianDepth(2);
    float invMedianDepth = 1.0f/medianDepth;
    
    //两个条件,一个是平均深度要大于0,另外一个是在当前帧中被观测到的地图点的数目应该大于100
    if(medianDepth<0 || pKFcur->TrackedMapPoints(1)<100)
    {
        cout << "Wrong initialization, reseting..." << endl;
        Reset();
        return;
    }

    // Step 6 将两帧之间的变换归一化到平均深度1的尺度下
    // Scale initial baseline
    cv::Mat Tc2w = pKFcur->GetPose();
    // x/z y/z 将z归一化到1 
    Tc2w.col(3).rowRange(0,3) = Tc2w.col(3).rowRange(0,3)*invMedianDepth;
    pKFcur->SetPose(Tc2w);

    // Scale points
    // Step 7 把3D点的尺度也归一化到1
    // 为什么是pKFini? 是不是就算是使用 pKFcur 得到的结果也是相同的? 答：是的，因为是同样的三维点
    vector<MapPoint*> vpAllMapPoints = pKFini->GetMapPointMatches();
    for(size_t iMP=0; iMP<vpAllMapPoints.size(); iMP++)
    {
        if(vpAllMapPoints[iMP])
        {
            MapPoint* pMP = vpAllMapPoints[iMP];
            pMP->SetWorldPos(pMP->GetWorldPos()*invMedianDepth);
        }
    }

    //  Step 8 将关键帧插入局部地图，更新归一化后的位姿、局部地图点
    mpLocalMapper->InsertKeyFrame(pKFini);
    mpLocalMapper->InsertKeyFrame(pKFcur);

    mCurrentFrame.SetPose(pKFcur->GetPose());
    mnLastKeyFrameId=mCurrentFrame.mnId;
    mpLastKeyFrame = pKFcur;

    mvpLocalKeyFrames.push_back(pKFcur);
    mvpLocalKeyFrames.push_back(pKFini);
    // 单目初始化之后，得到的初始地图中的所有点都是局部地图点
    mvpLocalMapPoints=mpMap->GetAllMapPoints();
    mpReferenceKF = pKFcur;
    //也只能这样子设置了,毕竟是最近的关键帧
    mCurrentFrame.mpReferenceKF = pKFcur;

    mLastFrame = Frame(mCurrentFrame);

    mpMap->SetReferenceMapPoints(mvpLocalMapPoints);

    mpMapDrawer->SetCurrentCameraPose(pKFcur->GetPose());

    mpMap->mvpKeyFrameOrigins.push_back(pKFini);

    mState=OK;// 初始化成功，至此，初始化过程完成
}

2.2.2 总体思路解析 

        我们认为单目初始化时候的参考帧和当前帧都是关键帧

        ①我们对单目初始化的第一帧和第二帧构造成关键帧pKFini 、pKFcur，并计算他们的Bow向量（BowVector、FeatureVector）

        ②将关键帧pKFini 、pKFcur插入到地图mnmap中。

        ③用初始化得到的3D点来生成地图点MapPoints，包括以下步骤：对跟踪初始化时前两帧之间的匹配mvIniMatches进行遍历。

        若没有匹配，则跳过。有匹配的情况对应于mvIniMatches[i] = j

        对有匹配点构造的世界坐标点构造地图点

MapPoint* pMP = new MapPoint(worldPos,pKFcur, mpMap);

        对第一帧第二帧分别添加构造的地图点pMp（让帧能看到该地图点）

pKFini->AddMapPoint(pMP,i);
pKFcur->AddMapPoint(pMP,mvIniMatches[i]);

        该MapPoint可以被哪个KeyFrame的哪个特征点观测到（让地图点能看见帧）

pMP->AddObservation(pKFini,i);
pMP->AddObservation(pKFcur,mvIniMatches[i]);

        从众多观测到该MapPoint的特征点中挑选最有代表性的描述子

pMP->ComputeDistinctiveDescriptors();

        更新该MapPoint平均观测方向以及观测距离的范围

pMP->UpdateNormalAndDepth();

        更新每个特征点对应的MapPoint，如果特征点没有对应的地图点，那么将存储一个空指针。

mCurrentFrame.mvpMapPoints[mvIniMatches[i]] = pMP;

        将该特征点属于外点的特征点标记置为false

 mCurrentFrame.mvbOutlier[mvIniMatches[i]] = false;

        将地图能看见地图点

mpMap->AddMapPoint(pMP);

        ④更新关键帧间的连接关系，在3D点和关键帧之间建立边，每个边有一个权重，边的权重是该关键帧与当前帧公共3D点的个数。

        ⑤全局BA优化，同时优化所有位姿和三维点

        ⑥取场景的中值深度，用于尺度归一化 

        ⑦把3D点的尺度也归一化到1

        ⑧将关键帧插入局部地图，更新归一化后的位姿、局部地图点

        ⑨置位单目初始化成功状态state位OK。

2.3 MapPoint::ComputeDistinctiveDescriptors函数解析

2.3.1 函数作用

        计算地图点最具代表性的描述子。由于一个地图点会被许多相机观测到，因此在插入关键帧后，需要判断是否更新代表当前点的描述子 
         方法是先获得当前点的所有描述子，然后计算描述子之间的两两距离，最好的描述子与其他描述子应该具有最小的距离中值。

2.3.2 代码 

void MapPoint::ComputeDistinctiveDescriptors()
{
    // Retrieve all observed descriptors
    vector<cv::Mat> vDescriptors;

    map<KeyFrame*,size_t> observations;

    // Step 1 获取该地图点所有有效的观测关键帧信息
    {
        unique_lock<mutex> lock1(mMutexFeatures);
        if(mbBad)
            return;
        observations=mObservations;
    }

    if(observations.empty())
        return;

    vDescriptors.reserve(observations.size());

    // Step 2 遍历观测到该地图点的所有关键帧，对应的orb描述子，放到向量vDescriptors中
    for(map<KeyFrame*,size_t>::iterator mit=observations.begin(), mend=observations.end(); mit!=mend; mit++)
    {
        // mit->first取观测到该地图点的关键帧
        // mit->second取该地图点在关键帧中的索引
        KeyFrame* pKF = mit->first;

        if(!pKF->isBad())        
            // 取对应的描述子向量                                               
            vDescriptors.push_back(pKF->mDescriptors.row(mit->second));     
    }

    if(vDescriptors.empty())
        return;

    // Compute distances between them
    // Step 3 计算这些描述子两两之间的距离
    // N表示为一共多少个描述子
    const size_t N = vDescriptors.size();
	
    // 将Distances表述成一个对称的矩阵
    // float Distances[N][N];
	std::vector<std::vector<float> > Distances;
	Distances.resize(N, vector<float>(N, 0));
	for (size_t i = 0; i<N; i++)
    {
        // 和自己的距离当然是0
        Distances[i][i]=0;
        // 计算并记录不同描述子距离
        for(size_t j=i+1;j<N;j++)
        {
            int distij = ORBmatcher::DescriptorDistance(vDescriptors[i],vDescriptors[j]);
            Distances[i][j]=distij;
            Distances[j][i]=distij;
        }
    }

    // Take the descriptor with least median distance to the rest
    // Step 4 选择最有代表性的描述子，它与其他描述子应该具有最小的距离中值
    int BestMedian = INT_MAX;   // 记录最小的中值
    int BestIdx = 0;            // 最小中值对应的索引
    for(size_t i=0;i<N;i++)
    {
        // 第i个描述子到其它所有描述子之间的距离
        // vector<int> vDists(Distances[i],Distances[i]+N);
		vector<int> vDists(Distances[i].begin(), Distances[i].end());
		sort(vDists.begin(), vDists.end());

        // 获得中值
        int median = vDists[0.5*(N-1)];
        
        // 寻找最小的中值
        if(median<BestMedian)
        {
            BestMedian = median;
            BestIdx = i;
        }
    }

    {
        unique_lock<mutex> lock(mMutexFeatures);
        mDescriptor = vDescriptors[BestIdx].clone();       
    }
}

2.3.3 函数解析 

        mObservations是一个map<KeyFrame*,size_t>型向量，第一维取观测到该地图点的关键帧，第二维是该地图点在关键帧中的索引。

        我们遍历观测到该地图点的所有关键帧，对应的orb描述子，放到向量vDescriptors中。

        接着我们构造一个N\times N的矩阵Distances，维度是一共有多少个描述子即有多少关键帧能观测到当前地图点。Distances[i][j]与Distances[j][i]表示第i个描述子与第j个描述子的距离。

        我们对这个矩阵的每行进行遍历，即第i个描述子与其他描述子的汉明距离，我们将它排序取中值，遍历完N次后我们得到了一个描述子，这个描述子距离其他描述子有最小的距离中值，我们记录这个中值值为BestMedian，这个中值对应的索引为BestIdx。

        这个索引对应的描述子就是我们选择的这个地图点最具有代表性的地图点。

2.4 MapPoint::UpdateNormalAndDepth函数解析 

2.4.1 函数作用

        更新地图点的平均观测方向、观测距离范围。

2.4.2 代码 

void MapPoint::UpdateNormalAndDepth()
{
    // Step 1 获得观测到该地图点的所有关键帧、坐标等信息
    map<KeyFrame*,size_t> observations;
    KeyFrame* pRefKF;
    cv::Mat Pos;
    {
        unique_lock<mutex> lock1(mMutexFeatures);
        unique_lock<mutex> lock2(mMutexPos);
        if(mbBad)
            return;

        observations=mObservations; // 获得观测到该地图点的所有关键帧
        pRefKF=mpRefKF;             // 观测到该点的参考关键帧（第一次创建时的关键帧）
        Pos = mWorldPos.clone();    // 地图点在世界坐标系中的位置
    }

    if(observations.empty())
        return;

    // Step 2 计算该地图点的平均观测方向
    // 能观测到该地图点的所有关键帧，对该点的观测方向归一化为单位向量，然后进行求和得到该地图点的朝向
    // 初始值为0向量，累加为归一化向量，最后除以总数n
    cv::Mat normal = cv::Mat::zeros(3,1,CV_32F);
    int n=0;
    for(map<KeyFrame*,size_t>::iterator mit=observations.begin(), mend=observations.end(); mit!=mend; mit++)
    {
        KeyFrame* pKF = mit->first;
        cv::Mat Owi = pKF->GetCameraCenter();
        // 获得地图点和观测到它关键帧的向量并归一化
        cv::Mat normali = mWorldPos - Owi;
        normal = normal + normali/cv::norm(normali);                       
        n++;
    } 

    cv::Mat PC = Pos - pRefKF->GetCameraCenter();                           // 参考关键帧相机指向地图点的向量（在世界坐标系下的表示）
    const float dist = cv::norm(PC);                                        // 该点到参考关键帧相机的距离
    const int level = pRefKF->mvKeysUn[observations[pRefKF]].octave;        // 观测到该地图点的当前帧的特征点在金字塔的第几层
    const float levelScaleFactor =  pRefKF->mvScaleFactors[level];          // 当前金字塔层对应的尺度因子，scale^n，scale=1.2，n为层数
    const int nLevels = pRefKF->mnScaleLevels;                              // 金字塔总层数，默认为8

    {
        unique_lock<mutex> lock3(mMutexPos);
        // 使用方法见PredictScale函数前的注释
        mfMaxDistance = dist*levelScaleFactor;                              // 观测到该点的距离上限
        mfMinDistance = mfMaxDistance/pRefKF->mvScaleFactors[nLevels-1];    // 观测到该点的距离下限
        mNormalVector = normal/n;                                           // 获得地图点平均的观测方向
    }
}

2.4.3 函数解析  

        我们先用变量observations接收能观测到该地图点的所有关键帧及该地图点再该关键帧中的索引，pRefKF接收第一次创建该地图点的关键帧，Pos接收该地图点在世界坐标系中的位置。

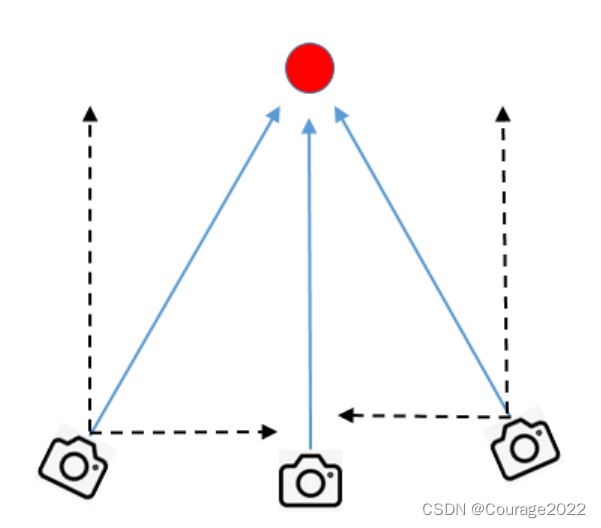
        接着我们遍历所有可以观测到该地图点的关键帧，提取能观测到该地图点的相机坐标与地图点坐标，形成指向地图点的向量并归一化进行累加normal。

         最后我们更新获得地图点平均的观测方向为（normal/能观测到该地图点的数量），并更新观测到该点的距离上限与观测到该点的距离下限。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/21957.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

idea使用谷歌翻译

idea使用谷歌翻译

项目场景&#xff1a; idea google翻译 问题描述 由于某些原因&#xff0c;现在谷歌翻译一直不能正常使用… 解决方案&#xff1a; 使用 pigcha 工具 设置也超级简单&#xff0c;每个月也就三十多块钱&#xff0c;可正常使用国内外网络。 电脑网络代理设置如下&#xff1a;…
阅读更多...
XSS平台与cookie获取

XSS平台与cookie获取

今天继续给大家介绍渗透测试相关知识&#xff0c;本文主要内容是XSS平台与cookie获取。 免责声明&#xff1a; 本文所介绍的内容仅做学习交流使用&#xff0c;严禁利用文中技术进行非法行为&#xff0c;否则造成一切严重后果自负&#xff01; 再次强调&#xff1a;严禁对未授权…
阅读更多...
[附源码]SSM计算机毕业设计大学生心理咨询网站JAVA

[附源码]SSM计算机毕业设计大学生心理咨询网站JAVA

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
【ElasticSearch学习笔记】一、ES下载、安装、目录结构、root用户权限问题、kibana下载安装

【ElasticSearch学习笔记】一、ES下载、安装、目录结构、root用户权限问题、kibana下载安装

下载和安装一、下载二、安装2.1 JDK的安装2.2 ElasticSearch的安装2.3 启动ES2.4 多节点启动三、Kibana的安装一、下载 以下载7.10.0为例&#xff1a; https://www.elastic.co/cn/downloads/elasticsearch 选择对应的操作系统&#xff0c;我是为了安装在CentOS上面&#xff0c…
阅读更多...
微信小程序 | 做一个小程序端的扫雷游戏

微信小程序 | 做一个小程序端的扫雷游戏

&#x1f4cc;个人主页&#xff1a;个人主页 ​&#x1f9c0; 推荐专栏&#xff1a;小程序开发成神之路 --【这是一个为想要入门和进阶小程序开发专门开启的精品专栏&#xff01;从个人到商业的全套开发教程&#xff0c;实打实的干货分享&#xff0c;确定不来看看&#xff1f; …
阅读更多...
【第三部分 | 移动端开发】3：Flex布局

【第三部分 | 移动端开发】3：Flex布局

目录 | Flex布局简介 | Flex父元素属性 设置主轴的方向 flex-direction 设置主轴上的子元素排列方式 justify-content 设置子元素是否换行 flex-wrap 设置侧轴上的子元素排列方式&#xff08;单行&#xff09; align-items 设置侧轴上的子元素的排列方式&#xff08;多行…
阅读更多...
HIve数仓新零售项目DWD层的构建

HIve数仓新零售项目DWD层的构建

HIve数仓新零售项目 注&#xff1a;大家觉得博客好的话&#xff0c;别忘了点赞收藏呀&#xff0c;本人每周都会更新关于人工智能和大数据相关的内容&#xff0c;内容多为原创&#xff0c;Python Java Scala SQL 代码&#xff0c;CV NLP 推荐系统等&#xff0c;Spark Flink Kaf…
阅读更多...
网络是怎样链接的--向DNS服务器查询Web服务器的IP地址

网络是怎样链接的--向DNS服务器查询Web服务器的IP地址

文章目录2.1 IP地址的基本知识2.2 域名和IP地址共用理由2.3 DNS本质是什么2.4 浏览器如何获取IP2.5 DNS解析器内部工作原理2.1 IP地址的基本知识 浏览器能够解析网址并生成HTTP消息&#xff0c;但并不具备将消息发送到网络中的功能&#xff0c;因此这一功能需要委托操作系统来…
阅读更多...
DataObjectImpl

DataObjectImpl

DataObjectImpl目录概述需求&#xff1a;设计思路实现思路分析1.DataObjectImpl2.DeadLetterJobQueryImpl3.DeploymentQueryImpl4.Direction5.DynamicBpmnServiceImpl参考资料和推荐阅读Survive by day and develop by night. talk for import biz , show your perfect code,fu…
阅读更多...
IDEA2022版本创建maven web项目（两种方式）

IDEA2022版本创建maven web项目（两种方式）

目录 一、使用骨架的方式 二、maven中添加 web方式 总结&#xff1a; 前言&#xff1a; 创建maven web项目有两种方式&#xff0c;一种是使用骨架方式&#xff0c;一种是不使用骨架的方式 一、使用骨架的方式 1.打开idea&#xff0c;按照步骤创建一个新的项目 2.点击Mave…
阅读更多...
【高级篇】Java JVM实战 之 内存调优

【高级篇】Java JVM实战 之 内存调优

文章目录一、通过Jprofiler调式Dump文件错误⛅ 什么是Jprofiler&#xff1f;⚡使用Jprofiler调试Dump文件二、堆内存调优三、 GC垃圾回收器四、GC常用算法❄️引用计数法⛄复制算法♨️标记清除算法⛽标记压缩⚠️标记清除压缩五、JMM⛵小结一、通过Jprofiler调式Dump文件错误 …
阅读更多...
Spark 3.0 - 4.Pipeline 管道的工作流程

Spark 3.0 - 4.Pipeline 管道的工作流程

目录 一.引言 二.基本组件 三.Pipeline 基本流程 1.训练 Pipeline - Estimator 2.预测 Pipeline - Transformer 四.Pipeline 分解与构造 1.DataFrame 2.Transformer1 - Tokenizer 3.Transformer2 - HashingTF 4.Estimator - LR 5.Pipeline With ParamMap - Estimat…
阅读更多...
SpringCloud微服务（一）——Consul服务注册中心

SpringCloud微服务（一）——Consul服务注册中心

Consul服务注册中心 SpringCloud 中文官网&#xff1a;https://www.springcloud.cc/spring-cloud-consul.html Consul是一套开源的分布式服务发现和配置管理系统&#xff0c;Go语言开发。 Consul是一个服务网格&#xff08;微服务间的 TCP/IP&#xff0c;负责服务之间的网络…
阅读更多...
SharedPreferences存储

SharedPreferences存储

文章目录 前言 听说SharedPreferences存储技术快过时了&#xff0c;不过如果是单纯的使用的话&#xff0c;不费什么时间成本。 本文的Demo摘录自《第一行代码》。 一.什么是SharedPreferences SharedPreferences&#xff0c;一种通过使用键值对的方式来存储数据的技术。 二…
阅读更多...
【深入浅出Spring6】第八期——面向切面编程 AOP

【深入浅出Spring6】第八期——面向切面编程 AOP

AOP&#xff08;Aspect Oriented Programming&#xff09;面向切面编程&#xff0c;属于面向对象编程的一种衍射&#xff0c;是一种编程思想或技术AOP的底层是由动态代理机制实现的 JDK动态代理CGLIB动态代理&#xff0c;自动识别并切换我们也可以通过配置属性指定就是用CGLIB …
阅读更多...
【MySQL】六，sql_model的合理设置

【MySQL】六，sql_model的合理设置

宽松模式和严格模式 宽松模式 如果设置的是宽松模式&#xff0c;那么我们在插入数据的时候&#xff0c;即使是给了一个错误的数据&#xff0c;那么可能也不会报错。 举例&#xff1a;某张表的name字段为 char(10) &#xff0c;插入数据的时候&#xff0c;如果name字段的数据长…
阅读更多...
免费搜题系统

免费搜题系统

免费搜题系统 本平台优点&#xff1a; 多题库查题、独立后台、响应速度快、全网平台可查、功能最全&#xff01; 1.想要给自己的公众号获得查题接口&#xff0c;只需要两步&#xff01; 2.题库&#xff1a; 查题校园题库&#xff1a;查题校园题库后台&#xff08;点击跳转&a…
阅读更多...
跨模态神经搜索实践VCED 基于Streamlit实现前端页面设计和逻辑

跨模态神经搜索实践VCED 基于Streamlit实现前端页面设计和逻辑

1. Streamlit入门 1.1 Streamlit介绍 Streamlit是基于Python的Web应用程序框架&#xff0c;它可以使用Python代码轻松构建机器学习/数据科学相关的仪表板&#xff0c;其特点包括&#xff1a; 跨平台&#xff1a;支持Windows、macOS、Linux只需要掌握Python&#xff1a;不需要…
阅读更多...
【时序】时间序列数据预处理

【时序】时间序列数据预处理

目录 1. 时间戳转换 2. 缺失值处理 3. 去噪 1&#xff09;滚动平均值 2&#xff09;傅里叶变换 4. 异常点检测 1&#xff09;基于滚动统计的方法 2&#xff09;孤立森林 3&#xff09;K-means 聚类 为了分析预处理结果&#xff0c;我们后续使用 Kaggle 的 Air Passenge…
阅读更多...
【Python】发布一个简单好用的日志记录器bestlog

【Python】发布一个简单好用的日志记录器bestlog

需求 日志是非常重要的一个东西&#xff0c;我们往往习惯于在开发一个新项目的第一行代码时&#xff0c;就用 logging.info 代替 print&#xff0c;随时保持记录的好习惯&#xff0c;等代码上线以后也无需修改替换那些 print&#xff0c;直接开跑&#xff0c;有了完善的日志&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023