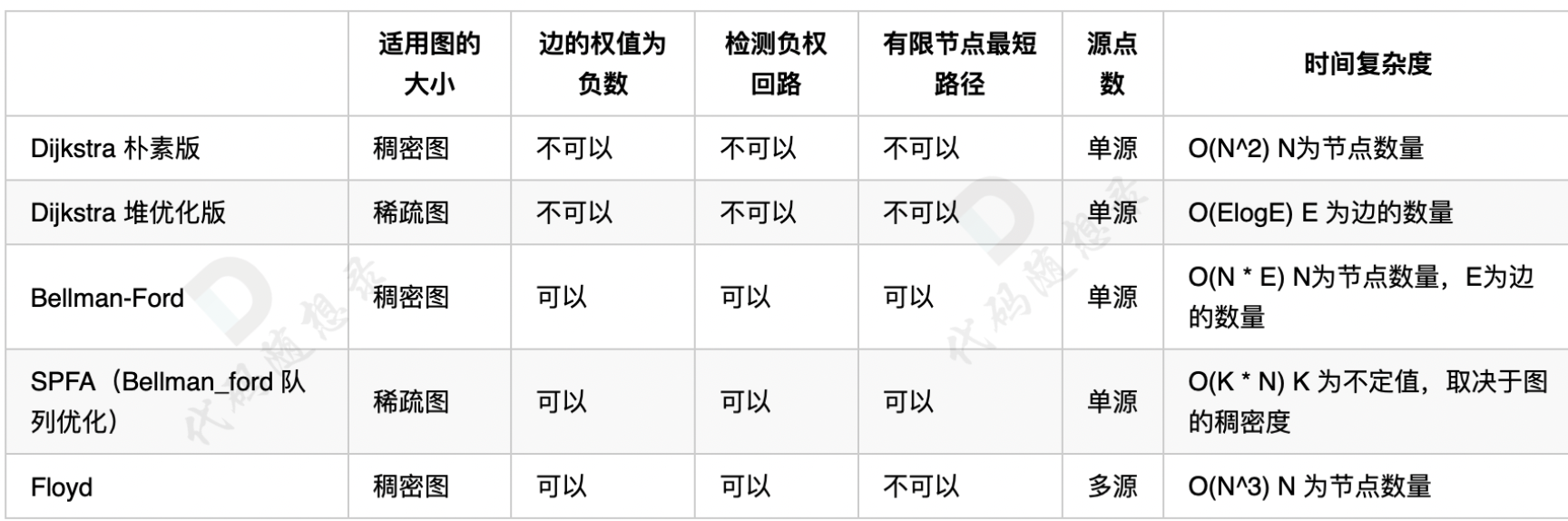
课程：b站王道数据结构 5.1.1 树的定义和基本术语_哔哩哔哩_bilibili

写在前面：基础不牢，地动山摇。。

一、树

1、概念

树是n（n>=0)个结点的有限集合，n=0时，称为空树

非空树的特性

有且仅有一个根节点

“叶子结点”（或终端结点）：没有后继的结点

“分支结点”（或非终端结点）：有后继的结点

除了根节点外，任何一个结点都有且仅有一个前驱

每个结点可以有0个或多个后继

当n>1时，其余结点可分为m（m>0)个互不相交的有限集合T1，T2，…，Tm,其中每个集合本身又是一棵树，并称为根结点的子树

树是一种递归定义的数据结构

结点之间的关系

祖先结点  子孙结点  双亲结点（父结点） 孩子结点  兄弟结点  堂兄弟结点

两个结点之间的路径  路径长度

结点、树的属性描述

结点的层次（深度）——从上往下数

结点的高度——从下往上数

树的高度（深度）——总共多少层

结点的度——有几个孩子（分支）非叶子结点>0 叶子结点=0

树的度——各结点的度的最大值

有序树、无序树

有序树，逻辑上看，树中结点的各子树从左至右是有次序的，不能互换

森林

m(m>=0)棵互不相交的树的集合

2、性质

（1）结点和度

结点数=总度数+1（总度数其实就是分支的总数量，只有根节点头上没有分支，所以是总度数+1）

度为m的树、m叉树的区别

树的度——各结点的度的最大值

度为m的树  任意结点的度<=m（最多m个孩子） 

至少有一个结点度=m(有m个孩子）一定是非空树，至少有m+1个结点 

m叉树——每个结点最多只能有m个孩子的树

任意结点的度<=m(最多m个孩子)

允许所有结点的度都<m  可以是空树

度为m的树第i层至多有个结点(i>=1)

eg m=3, 第1层1个结点，第2层3个结点，第3层3*3=......

m叉树第i层至多有个结点(i>=1)

（2）结点和高度

高度为h的m叉树至多有个结点

计算过程： 等比求和 

高度为h的m叉树至少有h个结点，高度为h、度为m的树至少有h+m-1个结点

(除了某一层为m，其他每一层为1）

具有n个结点的m叉树的最小高度为

计算过程：

3、存储

①双亲表示法（顺序）

5.4_1_树的存储结构_哔哩哔哩_bilibili

struct TreeNode{
    int data;
    int parent;
}

• 优点：查指定结点的双亲很方便  缺点：查指定结点的孩子只能从头遍历

②孩子表示法（顺序+链式）

struct CTNode{
    int child;//孩子结点在数组中的位置
    struct CTode *next;//下一个孩子
}；
typedef struct{
    int data;
    struct CTNode *firstChild;//第一个孩子
}CTBox；

③孩子兄弟表示法（链式）

typedef struct CSNode{
    int data;
    struct CSNode *firstchild,*nextsibling;//第一个孩子和右兄弟指针
}CSNode,*CSTree;

二、二叉树

1、概念

每个结点至多只有两棵子树

左右子树不能颠倒（二叉树是有序树）

二叉树的五种状态 ：空二叉树  只有左子树  只有右子树  只有根节点  左右子树都有

2、性质

（1）n0=n2+1

设非空二叉树中度为0、1和2的结点个数分别为n0、n1和n2,则n0=n2+1(叶子结点比二分支结点多一个)

计算过程：

n=n0+n1+n2  n=n1+2*n2+1 -> n0=n2+1

（2）第i层至多有个结点(i>=1)

（3）高度为h的二叉树至多有个结点（满二叉树）

高度为h的m叉树至多有个结点

3、几种特殊的二叉树

（1）满二叉树

高度为h，且含有个结点的二叉树

只有最后一层有叶子结点

不存在度为1的结点

按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1, 结点i的父节点为 i/2

（2）完全二叉树

当且仅当每个结点都与高度为h的满二叉树中编号1~n的结点一一对应时，称为完全二叉树

只有最后两层可能有叶子结点

最多只有一个度为1的结点

按层序从1开始编号，结点i的左孩子为2i，右孩子为2i+1, 结点i的父节点为[i/2]

i<=[n/2]为分支结点，i>[n/2]为叶子结点

(因为n的父结点是[n/2])

如果某结点只有一个孩子，那么一定是左孩子

性质：

① 具有n个（n>0）结点的完全二叉树的高度h为或

计算过程：

高度为h最大结点数：

最小结点数：

② n0=n2+1->n0+n2一定是奇数

完全二叉树最多只有一个度为1的结点，即n1=0或1

（3）二叉排序树

左子树上所有结点的关键字均小于根结点的关键字

右子树上所有结点的关键字均大于根结点的关键字

左子树和右子树又各是一棵二叉排序树

可用于元素的排序、搜索

（4）平衡二叉树

树上任一结点的左子树和右子树的深度之差不超过1

有更高的搜索效率

4、存储结构

（1）顺序存储

就是用数组来描述

定义结点

struct TreeNode{
int data;
bool isEmpty;
}

存放在数组

TreeNode t[MaxSize];
for(int i=1;i<MaxSize;i++){//可以让第一个位置空缺，保证数组下标和结点编号一致
    t[i].isEmpty=true;//初始化时所有结点标记为空
    t[i].data
}

顺序存储中一定要把二叉树的结点编号与完全二叉树对应起来

结论：二叉树的顺序存储结构，只适合存储完全二叉树

（2）链式存储

用链表

定义结点

struct TreeNode{
    int data;
    struct TreeNode *lchild, *rchild;//孩子表示法

    TreeNode(int val):data(val),left(nullptr),right(nullptr){} 
};

创建二叉树

TreeNode* Create(){
    int val; 
    cin >> val;
    if(val == '#') return nullptr; //空结点

    TreeNode* newNode = new TreeNode(val);
    //cout<<"enter lchild of :"<<val ;
    newNode -> lchild = Create();
    //cout<<"enter rchild of :"<<val ;
    newNode -> rchild = Create();

    return newNode;
}

//三叉链表——方便找父结点
    typedef struct TreeNode{
    int data;//数据域
    struct TreeNode *lchild,*rchild;//左、右孩子指针
    struct TreeNode *parent;// 父结点指针
    }BiNode,*BiTree;

5、二叉树的遍历 重点！！

（1）先序遍历

根 -> 左 -> 右

  - + a * b - c d / e f

递归

void PreOrderRecursive(TreeNode* root){
    if ( root == nullptr ) return;
    cout << root->data << " ";
    PreOrderRecursive (root -> lchild);
    PreOrderRecursive (root -> rchild);
}

非递归

众所周知，递归和栈有点关系👀

void PreOrderNotRecursive(TreeNode* root){
    if ( root == nullptr ) return;
    stack<TreeNode*>s;
    s.push(root);//入栈
    while(!s.empty()){
        TreeNode* node = s.top();//栈顶元素

        s.pop();//出栈
        cout << node->data ;
        if(node -> rchild )//右晚出 
            s.push(node -> rchild);
        if(node ->lchild )//左先出 
            s.push(node -> lchild);
    }

这里可以看：45 二叉树的非递归遍历代码实现_哔哩哔哩_bilibili

（2）中序遍历

 a + b * c - d - e / f

递归

void InOrderRecursive(TreeNode* root){
    if ( root == nullptr ) return;

    InOrderRecursive (root -> lchild);
    cout << root->data << " ";
    InOrderRecursive (root -> rchild);
}

非递归

void InOrderNotRecursive(TreeNode* root){
    //if ( root == nullptr ) return;

    stack<TreeNode*>s;
    TreeNode* curr = root;
    while(curr || !s.empty())
        { while(curr){
            s.push(curr);
            curr = curr ->lchild;
            }
          curr =s.top();
          s.pop();
          cout<< curr -> data ;
          curr= curr->rchild;
        }
   }

（3）后序遍历

 a b c d - * + e f / -

 递归

void PostOrderRecursive(TreeNode* root){
    if ( root == nullptr ) return;

    PostRecursive (root -> lchild);
    PostRecursive (root -> rchild);
    cout << root->data << " ";
}

非递归

void PostOrderNotRecursive(TreeNode* root){
    if ( root == nullptr ) return;
    stack<TreeNode*>s1,s2;
    s1.push(root);
    while(!s1.empty())
    { TreeNode * node =s1.top(); s1.pop(); s2.push(node);
      if(node->lchild) s1.push(node->lchild);}
      if(node->rchild) s1.push(node->rchild);}
    }
    while(!s2.empty())
    {cout<<s2.top()->data; s2.pop()}
}

（4）层次遍历

用队列

void levelOrder(TreeNode* root){
    arrayQueue<TreeNode*>q;
    while(root ! =nullptr)
    {   
        cout<< root->data;//visit(root)
        if(root->lchild) q.push(root->lchild);
        if(root->rchild) q.push(root->rchild);

        try{t=q.front();}
        catch (queueEmpty){return;}
        q.pop();
    }
}

6、由遍历序列构造二叉树 重点！！

唯一确定一棵二叉树的几种情况：

前序+中序

    根        左子树     右子树

左子树          跟       右子树

eg 

Pre   A  D  B  C  E

In     B  D  C   A  E

Pre  D  B  C

In    B  D  C

后序+中序

层序+中序

同理，都是找根结点，左子树右子树去分析

7、应用

（1）求树的深度

int TreeHeight(TreeNode* root) {
    if (root == nullptr) {
        return 0;
    }
    int leftHeight = TreeHeight(root->lchild);
    int rightHeight = TreeHeight(root->rchild);
    return max(leftHeight, rightHeight) + 1;
}

（2）求叶子总数

int CountLeaves(TreeNode* root) {
    if (root == nullptr) {
        return 0;
    }
    if (root->lchild == nullptr && root->rchild == nullptr) {
        return 1;
    }
    return CountLeaves(root->lchild) + CountLeaves(root->rchild);
}