目录
1.二叉搜索树的最近公共祖先
2.二叉树中的插入操作
3.删除二叉搜索树中的节点
题目1、二叉搜索树的最近公共祖先
力扣题目链接(opens new window)
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
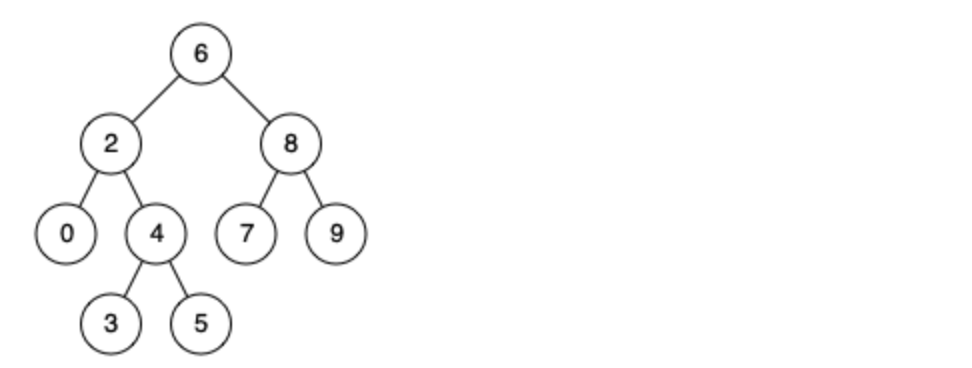
示例 1:
- 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
- 输出: 6
- 解释: 节点 2 和节点 8 的最近公共祖先是 6。
思路
我们从二叉搜索树的根节点开始遍历,通过判断传入的两个参数节点的值,与根节点的值的大小关系,然后判断从根节点的左子树还是右子树开始搜索,如果遍历到叶子结点时还没有搜索到参数节点的值,我们就可以返回NULL;我们可以使用递归的思路求解, 最终的返回值是对应的root。
代码实现
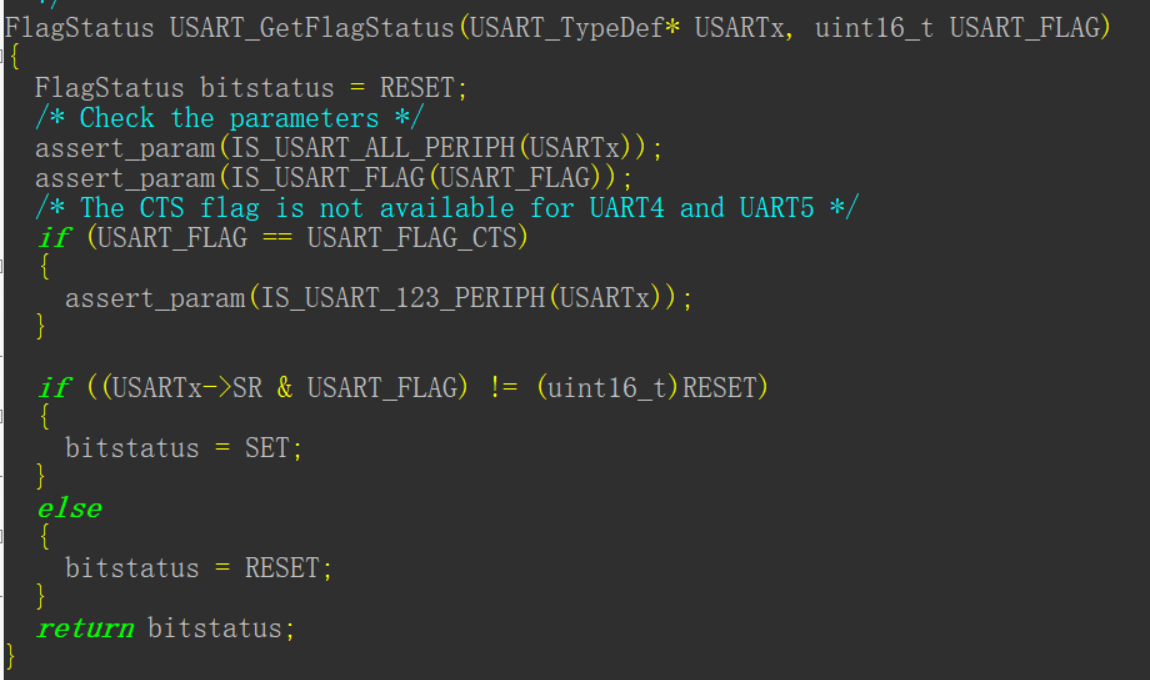
CPP
执行逻辑主要包括三种:p、q的值都比当前节点值大;p、q的值都比当前节点值小;p、q在当前节点的一左一右
class Solution {
private:
TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q) {
if (cur == NULL) return cur;
// 中
if (cur->val > p->val && cur->val > q->val) { // 左
TreeNode* left = traversal(cur->left, p, q);
if (left != NULL) {
return left;
}
}
if (cur->val < p->val && cur->val < q->val) { // 右
TreeNode* right = traversal(cur->right, p, q);
if (right != NULL) {
return right;
}
}
return cur;
}
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
return traversal(root, p, q);
}
};Python
class Solution:
def lowestCommonAncestor(self, root, p, q):
if root.val > p.val and root.val > q.val:
return self.lowestCommonAncestor(root.left, p, q)
elif root.val < p.val and root.val < q.val:
return self.lowestCommonAncestor(root.right, p, q)
else:
return root题目2、二叉树中的插入操作
力扣题目链接(opens new window)
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据保证,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

思路
对于二叉搜索树中的插入操作,我能不能把二叉搜索树先转换成有序数组,再把给定的整数插入转换后的有序数组,最后进行中序遍历来得到新的二叉搜索树?
理论上可行,但是显然不是最优解。
-
时间复杂度:
- 转换BST为有序数组:这个操作需要中序遍历BST,时间复杂度为O(n),其中n是BST的节点数。
- 在有序数组中插入元素:在有序数组中插入一个元素需要找到正确的位置,并可能移动其他元素,时间复杂度为O(n)。
- 从有序数组重建BST:将有序数组转换为BST的过程(例如,使用递归的方式构建平衡BST)通常也有O(n)的时间复杂度。
综合起来,这个方法的总时间复杂度为O(n) + O(n) + O(n) = O(3n),即O(n)。虽然从表面上看这个时间复杂度与直接在BST中插入的时间复杂度O(log n)(在平衡BST中)或O(n)(在最坏情况下,如退化为链表)相比没有显著区别,但实际操作中会有额外的空间开销和步骤,且可能破坏BST的平衡性。
我们可以不考虑题目中提示所说的改变树的结构的插入方式,只要按照二叉搜索树的规则去遍历,遇到空节点就插入节点就可以了。
代码实现
CPP
假如遇到空节点,我们直接插入并返回该节点;假如当前节点的值大于要插入的值,我们在左子树进行插入操作,否则在右子树操作。我们可以使用递归的思路。
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
if (root->val > val) root->left = insertIntoBST(root->left, val);
if (root->val < val) root->right = insertIntoBST(root->right, val);
return root;
}
};python
class Solution:
def insertIntoBST(self, root, val):
if root is None:
node = TreeNode(val)
return node
if root.val > val:
root.left = self.insertIntoBST(root.left, val)
if root.val < val:
root.right = self.insertIntoBST(root.right, val)
return root题目3、删除二叉搜索树中的节点
力扣题目链接(opens new window)
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点; 如果找到了,删除它。 说明: 要求算法时间复杂度为 $O(h)$,h 为树的高度。
示例:

思路
首先我们自然地回去想找到需要删除的节点,如果找到目标节点,我们就删除它。但是我们要考虑节点是叶子结点、只拥有左子树/右子树的节点、根节点的情况,听上去会比较复杂。
分类讨论:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
代码实现
CPP
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) return root; // 第一种情况:没找到删除的节点,遍历到空节点直接返回了
if (root->val == key) {
// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
if (root->left == nullptr && root->right == nullptr) {
///! 内存释放
delete root;
return nullptr;
}
// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点
else if (root->left == nullptr) {
auto retNode = root->right;
///! 内存释放
delete root;
return retNode;
}
// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
else if (root->right == nullptr) {
auto retNode = root->left;
///! 内存释放
delete root;
return retNode;
}
// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
// 并返回删除节点右孩子为新的根节点。
else {
TreeNode* cur = root->right; // 找右子树最左面的节点
while(cur->left != nullptr) {
cur = cur->left;
}
cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置
TreeNode* tmp = root; // 把root节点保存一下,下面来删除
root = root->right; // 返回旧root的右孩子作为新root
delete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)
return root;
}
}
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};python
class Solution:
def deleteNode(self, root, key):
if root is None: # 如果根节点为空,直接返回
return root
if root.val == key: # 找到要删除的节点
if root.right is None: # 如果右子树为空,直接返回左子树作为新的根节点
return root.left
cur = root.right
while cur.left: # 找到右子树中的最左节点
cur = cur.left
root.val, cur.val = cur.val, root.val # 将要删除的节点值与最左节点值交换
root.left = self.deleteNode(root.left, key) # 在左子树中递归删除目标节点
root.right = self.deleteNode(root.right, key) # 在右子树中递归删除目标节点
return root#如果二叉搜索树改成普通二叉树,思路和代码实现又会变得不同