1.题目报告
| 1.交替出场 | 2.翻翻转转 | 3.方格取数 | 4.圆圆中的方方 |
| AC | 0分--文件读写 | 0分 | 20分--骗分 |
2.赛中概况
第一题比较顺利,五六分钟就开始敲代码,暴力AC。
第二题耗了30分钟左右才有思路,写的时候也不大顺利,用得递归。文件读写错了,0分(写对是20分)。递归调用条件也错了,该用那个左移,取反也只需要一个log2的。
第三、四题根本没仔细看,本来骗分能拿50分的,最后只拿了20分。
赛后1,2,3题AC,
3.题目分析:
1.交替出场
题目描述
给定一个字符串,仅包含字符
0或1,求字符串中的01交替子串个数。
01交替串的定义是,前一位必须不同于后一位的字符串。特殊的,任意的长度为
1的字符串也被定义为01交替串。输入描述
一行,一个字符串 ss,保证仅包含字符
0或1。输出描述
一行一个整数,表示 ss 中的
01交替子串个数。输入样例
0101输出样例
10样例解释
显然的,任意一个子串都是
01交替子串。数据范围
定义 nn 为字符串 ss 的长度。
对于 20%20% 数据:1≤n≤3。对于另外 60%60% 数据:1≤n≤100。
对于全部数据:1≤n≤1000。
比赛情况:AC
分析:
这道题直接暴力就能过,主要分两种:1.按字符串长度分类判断,时间复杂度O(n^3),较高;
2.按起点终点分类,(确定起点找终点)时间复杂度O(n^2)
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=100500;
int main(){
//freopen("alter.in","r",stdin);
//freopen("alter.out","w",stdout);
string a;
cin>>a;
int len=a.size(),sum=0;
for(int i=0;i<len;i++){
for(int j=i;j<len;j++){
if(j-i==0)sum++;
else{
if(a[j-1]!=a[j]){
sum++;
}else{
break;
}
}
}
}cout<<sum;
return 0;
}2. 翻翻转转
题目描述
gza 有一系列的字符串,第 ii 个名为 sisi。
s0=1
s1=10
s2=1001
s3=10010110
⋯⋯
si 是 si−1 逐位取反后拼接在 si−1 后的串。
你需要求 s114514 的第 x 个字符是什么。
多测。
输入描述
第一行一个整数 TT,表示数据组数。
接下来 TT 行,一行一个整数,表示 x,含义见题目描述。
输出描述
一共 TT 行,一行一个字符,表示答案。
输入样例
1
3输出样例
0数据范围
对于 10% 的数据:x≤100。
对于另外 50% 的数据:x≤10^7。
对于全部数据:x≤10^9。
分析:
这道题用递归求解,从样例中找规律可知 :
s[2]=~s[1]
s[3]=~s[1] s[4]=~s[2]
s[5]=~s[1] s[6]=~s[2] s[7]=~s[3] s[8]=~s[4]
......
推算得出:
s[2^n+t]=~s[2^(n-1)+t]
也就是说是是s[t]=s[1<<log(t)-1]或s[t-(1<<log(t))]
得代码 :
#include<bits/stdc++.h>
using namespace std;
const int N=100500;
long long a[]={};
bool pre(int n){
if(n==1)return 1;
int k=log2(n);
if(1<<k==n)return !pre(1<<k-1);
else{
return !pre(n-(1<<k));
}
}
int main(){
long long t;
cin>>t;
while(t--){
long long x;
cin>>x;
long long p=log2(x),cnt=1;
for(int i=1;i<=p;i++){
cnt*=2;
}
cout<<pre(x)<<endl;
}
return 0;
}3.方格取数
大意:
第 1 行三个正整数 n,m,k。
接下来 nn 行每行 mm 个整数,依次代表每个方格中的整数。
从 (1,1)出发,目标是 (n,m),只能向右或者向下走,但是你不能一次性往一个方向走大于等于 k 步。
求收集到的数字的和的最大值。
解析
看上去用DFS能A。但因为'k'的原因只能拿60pts,正解需用dp。
定义一个三维数组,分别存储在(i,j)的坐标上最大的收益,第三维为0/1(1表示必须改变方向),注释↓
AC:
#include<iostream> using namespace std; typedef long long ll; const long long N=200,MIN=-1e18; ll n,m,k,a[N+5][N+5],dp[N+5][N+5][2],ans=MIN; /*不能连续往一个方向走k步,刷新方向后步数会重置 由于是在一个矩阵图形中进行移动并计算权值和,可以使用dfs 搜索或遍历所有的路径,计算所有路径的权值和 需要额外记录按照一个方向走的步数和当前权值和(可能有负数) void dfs(int x,int y,int down,int right,ll sum){ if(x==n&&y==m){ ans=max(ans,sum); return ; } if(x<n && down+1<k) dfs(x+1,y,down+1,0,sum+a[x+1][y]); if(y<m && right+1<k)dfs(x,y+1,0,right+1,sum+a[x][y+1]); } int main(){ cin>>n>>m>>k; n=m=k=200; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++) cin>>a[i][j]; } dfs(1,1,0,0,a[1][1]); if(ans==-1e18) cout<<"No Answer!"; else cout<<ans; return 0; } */ int main(){ /*dp[i][j][1/0]:到达第i行,第j列所经过数字之和的最大值, 其中1代表是从上往下到达i,j,0代表从左往右到达i,j 到达第i行,第j列: 1、可能是从上往下,每次走1步,连走1步,2步,3步...k步; 所以设d[t]:代表从上往下,连走t步所经过的数字之和的最大值 由此可得d[t] = dp[i - t][j] + sumt; //sumt代表从第i - t + 1行到第i行的所有数字之和; dp[i][j][1] = max(d[t]); 2、可能是从左往右,每次走1步,连走1步,2步,3步...k步; 所以设r[t]:代表从左往右,连走t步所经过的数字之和的最大值 由此可得r[t] = dp[i][j - t] + sumr; //sumr代表从第j - t + 1列到第j列所有数字之和; dp[i][j][0] = max(r[t]); 所以ans = max(dp[i][j][1],dp[i][j][0]); 1 <= t <= k - 1 */ cin>>n>>m>>k; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ cin>>a[i][j]; dp[i][j][1]=dp[i][j][0]=MIN; } } for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(i==1&&j==1){ dp[i][j][1]=dp[i][j][0]=a[1][1];//处理起点 continue; } ll sumd=0,sumr=0,maxd=MIN,maxr=MIN; for(int t=1;i-t>=1&&t<=k-1;t++){ //从上往下 sumd+=a[i-t+1][j]; maxd=max(maxd,dp[i-t][j][0]+sumd); //dp[i - t][j][0]代表从左到右到达i - t,j } dp[i][j][1]=maxd; for(int t=1;j-t>=1&&t<=k-1;t++){ //从左往右 sumr+=a[i][j-t+1]; maxr=max(maxr,dp[i][j-t][1]+sumr); //dp[i][j - t][1]代表从上到下到达i,j - t } dp[i][j][0]=maxr; } } ans=max(dp[n][m][1],dp[n][m][0]); if(ans<=-99600000) cout<<"No Answer!"; else cout<<ans; return 0; }赛后AC
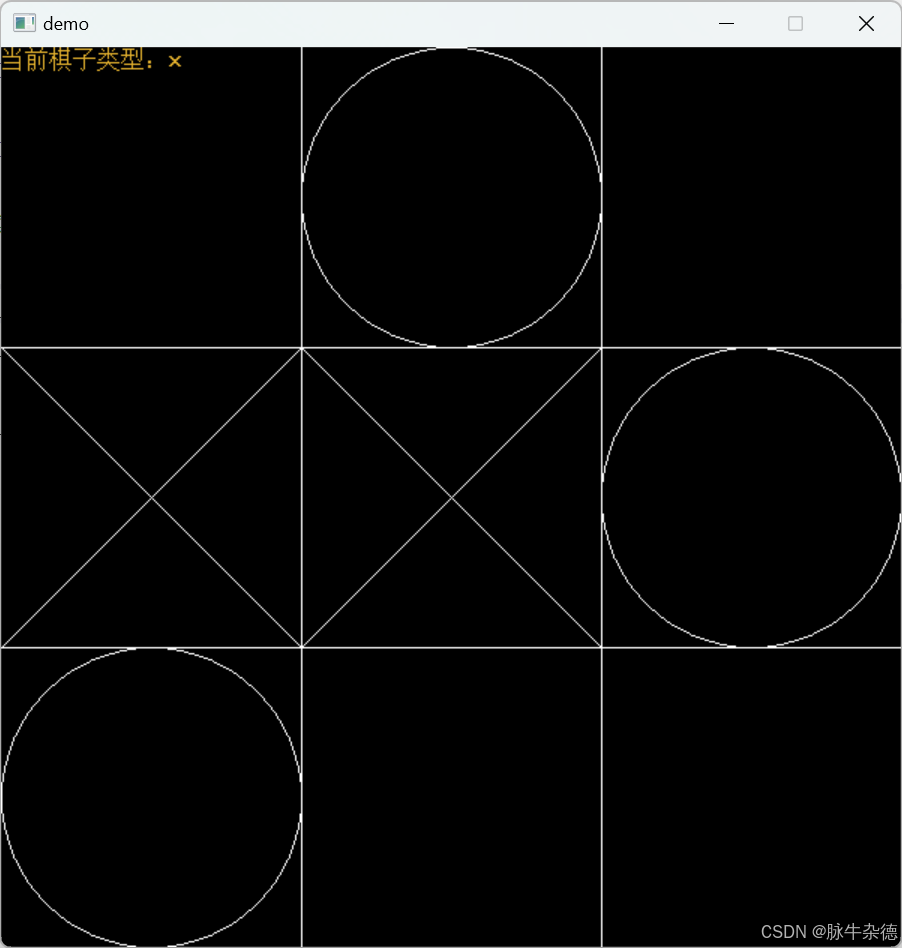
4.圆圆中的方方
题目意思:给定了一个圆和一个矩形,求两个面积交。
sub1
就是样例,送分。
sub2
狗吠:长度超过了矩形对角线长,因此,矩形完全包含在了圆中。答案就是矩形面积。
sub3
狗吠:整个圆都包含在了矩形中,因此圆的面积就是答案。
sub4、sub5
需要考虑到正解,但是因为细节实现复杂,设置这部分分。
sub6
考虑将整块面积分为四部分,圆心的左上,圆心的左下,圆心的右上,圆心的右下。那么问题将转化为:一个圆心在角落的 圆与矩形的面积交。经过一系列对称后可以保证与下图同构。

容易把问题划分成四种情况。

第一种和最后一种是平凡的,二三可以使用三角函数辅助计算。第二种情况:
左边三角形面积加上扇形面积。
扇形面积可以通过求扇形角度后得到。

第三种情况:
与情况二分析过程类似。

#include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1), eps = 1e-6;
double n, m, x, y, r;
double calc(double n, double m, double r) {
if (n > m)
swap(n, m);
if (n < eps || m < eps)
return 0;
if (r <= n)
return 0.25 * pi * r * r;
else if (r <= m) {
double tt = sqrt(r * r - n * n);double res = n * tt / 2.0;double ang = pi / 2 - acos(n / r);
res += ang / 2 * r * r;
return res;
} else if (r <= sqrt(n * n + m * m)) {
double t1 = sqrt(r * r - n * n), t2 = sqrt(r * r - m * m);double res = n * t1 / 2.0 + m * t2 / 2.0;double ang = pi / 2 - acos(n / r) - acos(m / r);
res += ang / 2 * r * r;
return res;
} else
return n * m;
}
int main() {
cin >> n >> m >> x >> y >> r;
cout << fixed << setprecision(10)
<< calc(x, y, r) + calc(x, m - y, r) + calc(n - x, y, r) +
calc(n - x, m - y, r)
<< endl;
return 0;
}











![[Unity Demo]从零开始制作空洞骑士Hollow Knight第十三集:制作小骑士的接触地刺复活机制以及完善地图的可交互对象](https://i-blog.csdnimg.cn/direct/00e9810fea774983b55668473d6b111c.png)



