目录
530.二叉搜索树的最小绝对差
501.二叉搜索树中的众数
236. 二叉树的最近公共祖先
530.二叉搜索树的最小绝对差
题目
530. 二叉搜索树的最小绝对差 - 力扣(LeetCode)
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例1:

输入:root = [4,2,6,1,3]
输出:1
示例2:

输入:root = [1,0,48,null,null,12,49]
输出:1
提示:
- 树中节点的数目范围是
[2, 104] 0 <= Node.val <= 105
思路
代码随想录:530.二叉搜索树的最小绝对差
视频讲解:LeetCode:530.二叉搜索树的最小绝对差
对于二叉搜索树,先使用中序遍历得到一个递增的有序序列,再使用双指针求相邻两个元素的差值。
题解
独立题解:
class Solution {
TreeNode pre = null;
public int getMinimumDifference(TreeNode root) {
if (root == null)
return Integer.MAX_VALUE;
int res = Integer.MAX_VALUE;
int left = getMinimumDifference(root.left);
if (pre == null) {
pre = root;
} else {
res = root.val - pre.val;
pre = root;
}
int right = getMinimumDifference(root.right);
return Math.min(Math.min(left, right), res);
}
}
使用全局变量res:
class Solution {
TreeNode pre;
int result = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
traversal(root);
return result;
}
public void traversal(TreeNode root){
if(root==null)return;
traversal(root.left);
if(pre!=null){
result = Math.min(result,root.val-pre.val);
}
pre = root;
traversal(root.right);
}
}
501.二叉搜索树中的众数
题目
501. 二叉搜索树中的众数 - 力扣(LeetCode)
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例1:
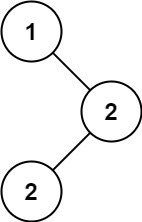
输入:root = [1,null,2,2]
输出:[2]
示例2:
输入:root = [0]
输出:[0]
提示:
- 树中节点的数目在范围
[1, 104]内 -105 <= Node.val <= 105
思路
代码随想录:501.二叉搜索树中的众数
视频讲解:LeetCode:501.二叉搜索树中的众数
- 由于二叉搜索树,考虑使用中序遍历,将二叉树转换为一个非严格递增序列。
- 使用双指针指向相邻的两个元素
- 同时定义两个全局变量,
count记录当前指向的相同元素出现次数,max记录当前的最大出现次数。 - 当
count==max时,将当前元素放入结果集,count>max时,清空结果集后放入当前元素,然后更新max
题解
双指针递归法:
class Solution {
List<Integer> list = new ArrayList<>();
int pre = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
int count = 0;
public int[] findMode(TreeNode root) {
getMode(root);
int[] res = new int[list.size()];
for (int i = 0; i < res.length; i++) {
res[i] = list.get(i);
}
return res;
}
void getMode(TreeNode root) {
if (root == null)
return;
getMode(root.left);
if (root.val == pre) {
count++;
} else {
count = 1;
}
if (count > max) {
list.clear();
list.add(root.val);
max = count;
} else if (count == max) {
list.add(root.val);
}
pre = root.val;
getMode(root.right);
return;
}
}
236. 二叉树的最近公共祖先
题目
236. 二叉树的最近公共祖先 - 力扣(LeetCode)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
- 树中节点数目在范围
[2, 105]内。 -109 <= Node.val <= 109- 所有
Node.val互不相同。 p != qp和q均存在于给定的二叉树中。
思路
代码随想录:236.二叉树的最近公共祖先
视频讲解:LeetCode:236. 二叉树的最近公共祖先
由题可以想到需要自底向上进行查找,而后序遍历是天然的回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
本题有两种情况:
情况一:找到一个节点,左子树中出现一个目标节点,右子树出现一个目标节点。如下图:
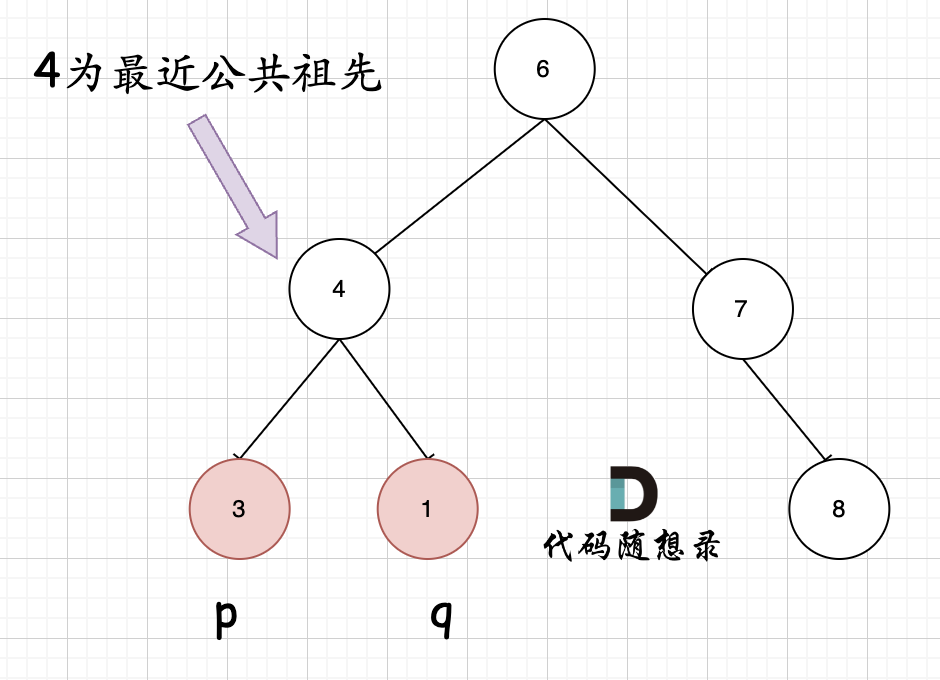
情况二:某个节点本身是一个目标节点,子树中还存在另一个目标节点。如下图:
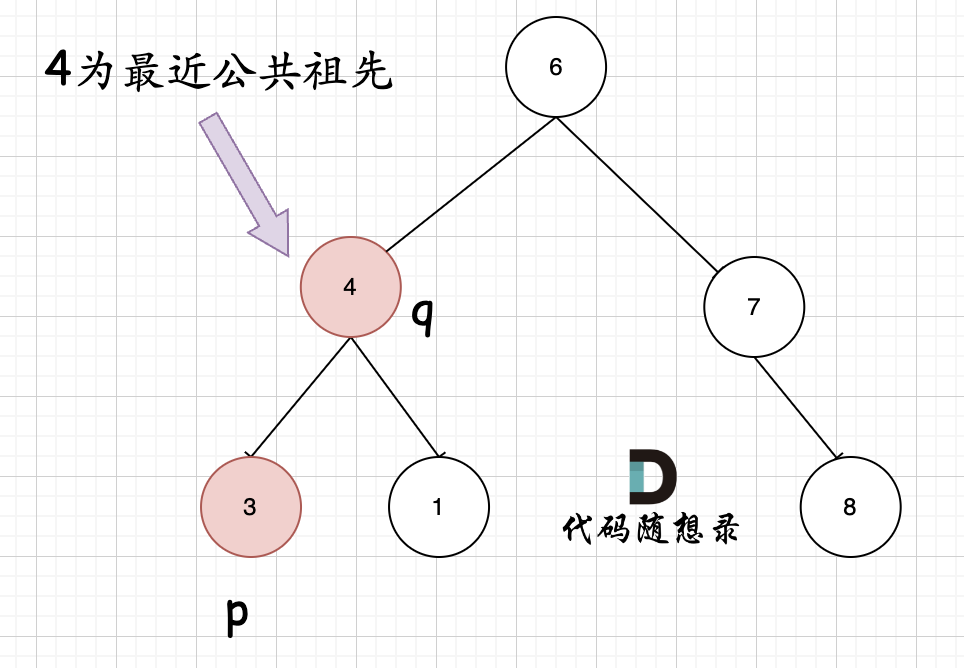
在本题中两种情况可以合并成同一种代码实现过程。
当遍历到某个节点时,首先判断该节点是否为目标节点,如果是则直接返回该节点,不是则继续递归,判断子树中是否存在目标节点。
题解
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 遇到空节点,返回null
if (root == null)
return null;
// 当前节点为目标节点,返回当前节点
if (root == q || root == p)
return root;
// 左
TreeNode left = lowestCommonAncestor(root.left, p, q);
// 右
TreeNode right = lowestCommonAncestor(root.right, p, q);
// 中
// 两个返回值都为空,说明当前节点子树不存在目标节点,返回null
if (left == null && right == null)
return left;
// 如果一个子树返回值为空,另一个不为空,说明找到了一个目标节点,返回非空节点
else if (left == null && right != null)
return right;
else if (left != null && right == null)
return null;
// 两个返回值都不为空,说明当前节点是目标节点的最近公共祖先
else
return root;
}
}
// 情况二:一直遍历到根节点,此时一边返回值null,另一边返回值为第一个遇到的目标节点,此时根节点返回该目标节点
// 所以情况一的代码实现也包含了情况二




![[Unity Demo]从零开始制作空洞骑士Hollow Knight第十三集:制作小骑士的接触地刺复活机制以及完善地图的可交互对象](https://i-blog.csdnimg.cn/direct/00e9810fea774983b55668473d6b111c.png)








![World of Warcraft [CLASSIC][80][Grandel] /console cameraDistanceMaxZoomFactor 2](https://i-blog.csdnimg.cn/direct/994f39a5ad1a403fb91b1fa946e77dc6.jpeg)