- **The term neuromorphic is generally used to describe analog, digital, mixed-mode analog/digital VLSI, and software systems that implement several models of neural systems.**
- 神经形态一词通常用于描述模拟、数字、混合模式的模拟/数字超大规模集成电路(VLSI)和实现多种神经系统模型的软件系统。
- 注释:VLSI(超大规模集成电路)指的是在单个芯片上集成大量电子元件的技术。
- **The implementation of neuromorphic computing on the hardware level can be realized by various technologies, including spintronic memories, threshold switches, CMOS transistors, and oxide-based memristors.**
- 神经形态计算在硬件层面的实现可以通过多种技术来实现,包括自旋电子存储器、阈值开关、CMOS晶体管和基于氧化物的忆阻器。
- 注释:CMOS(互补金属氧化物半导体)是一种常见的芯片制造技术,忆阻器是一种具有记忆功能的电子元件。
- **This introduces the neuromorphic computing systems and explores the fundamental concepts underlying this emerging paradigm.**
- 这里介绍神经形态计算系统,并探讨这一新兴范式的基本概念。
- **We first discuss biological neurons and the dynamics that are abstracted from them to model artificial neurons.**
- 我们首先讨论生物神经元以及从中抽象出来的动态用于建模人工神经元。
- **Next, we discuss artificial neurons and how they have evolved in their representation of biological neuronal dynamics.**
- 接下来,我们讨论人工神经元及其在表示生物神经元动态方面是如何演变的。
- **Afterward, we discuss implementing these neural networks in terms of neuron models, storage technologies, inter-neuron communication networks, and learning.**
- 之后,我们探讨如何从神经元模型、存储技术、神经元间通信网络和学习等方面实现这些神经网络。
### 1.1 Introduction
- **The human nervous system is composed of more than 100 billion cells known as neurons.**
- 人类神经系统由超过1000亿个被称为神经元的细胞组成。
- **The neurons perceive changes in the environment, convey these changes to other neurons, and directs body responses to these perceptions.**
- 神经元感知环境变化,将这些变化传递给其他神经元,并指导身体对这些感知的反应。
- **Because these neurons can carry out information processing in a rapid, parallel, fault-tolerant, and energy-efficient manner, it has received so much attention.**
- 由于这些神经元可以以快速、并行、容错和节能的方式进行信息处理,因此受到了极大的关注。
- **This chapter introduces the fundamentals of neuromorphic computing systems by discussing biological neurons and the dynamics abstracted from them to model artificial neurons.**
- 本章通过讨论生物神经元及从中抽象出的动态来介绍神经形态计算系统的基础知识。
- **Neuromorphic computing brain-inspired computing paradigm takes inspiration from the brain to develop energy-efficient circuits and systems for future information processing, capable of highly complicated tasks.**
- 神经形态计算是一种受大脑启发的计算范式,从大脑中汲取灵感,开发用于未来信息处理的节能电路和系统,能够完成高度复杂的任务。
- **Such computing promises to drastically improve the efficiency of critical computational tasks, such as decision-making and perception.**
- 这种计算有望大幅提高关键计算任务的效率,如决策和感知。
- **Unlike the typical artificial neural networks (ANNs), where neurons fire at each propagation cycle, the neurons in a brain-inspired neural network model, named spiking neural networks (SNNs), fire only when a membrane potential crosses a threshold value.**
- 与典型的人工神经网络(ANNs)中神经元在每个传播周期都会激发不同的是,受大脑启发的神经网络模型(称为脉冲神经网络,SNNs)中的神经元只有在膜电位超过阈值时才会激发。
- 注释:脉冲神经网络(SNNs)是一种更接近生物神经元行为的神经网络模型,采用脉冲形式的激发机制。
- **Spiking neurons are only activated**
- 脉冲神经元只有在特定条件下才会被激活。
- **When sufficient signals are integrated from other neurons, which leads to sparse neural activities at the network level.**
- 当来自其他神经元的足够信号被整合时,这会导致网络级别的稀疏神经活动。
- 注释:稀疏神经活动指的是在神经网络中,只有一小部分神经元在特定时间内被激发。
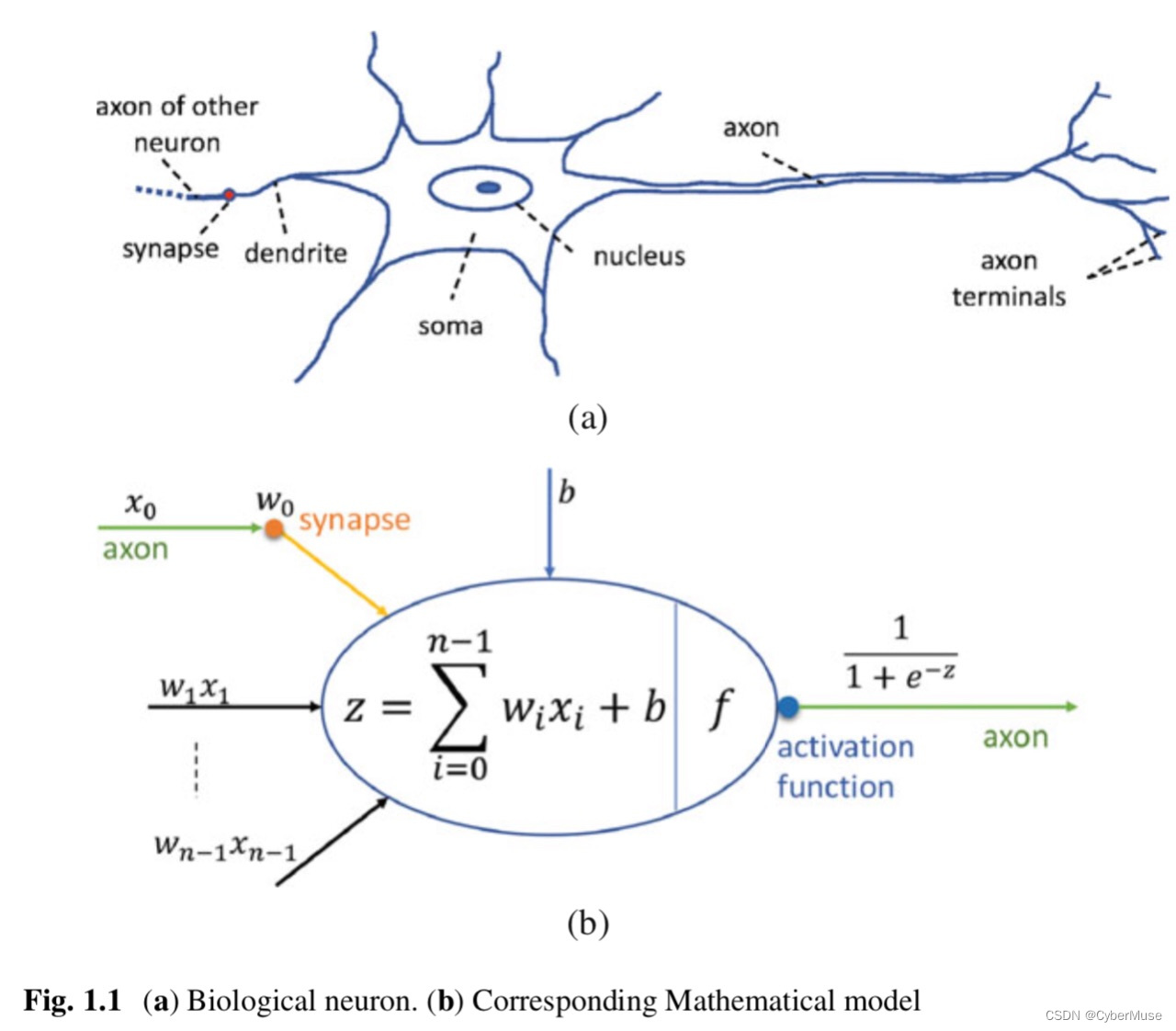
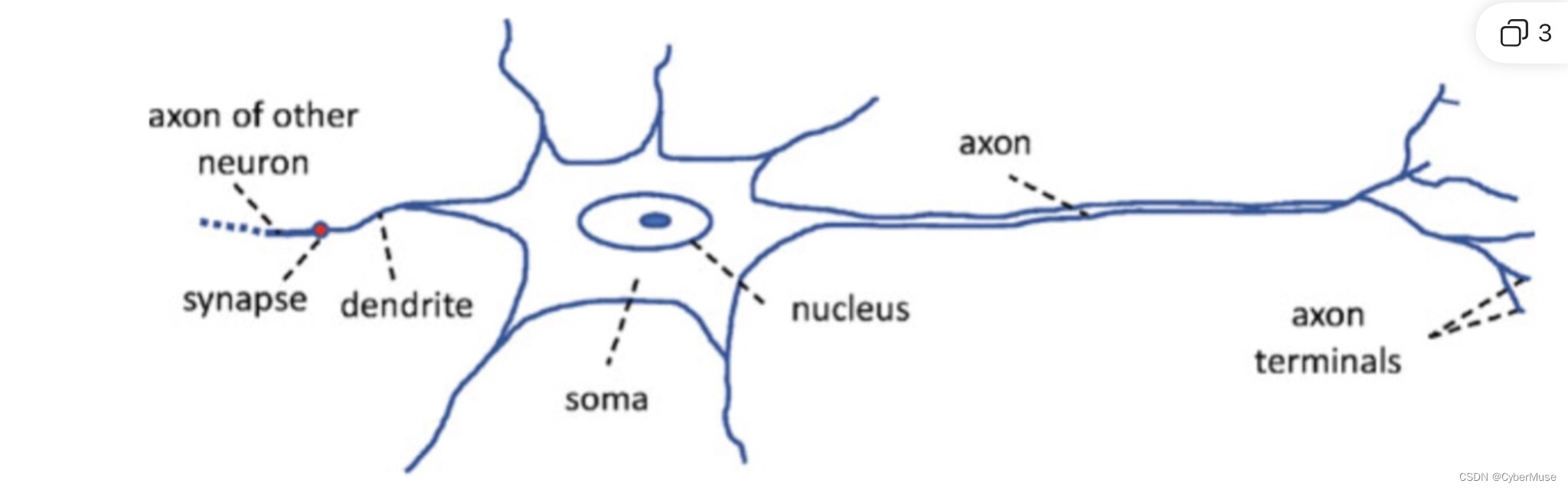
- **A general description of a biological neuron is presented in Fig. 1.1.**
- 图1.1展示了生物神经元的一般描述。
- **A neuron consists of several parts: The dendrite, the axon, and the soma.**
- 神经元由几个部分组成:树突、轴突和胞体。
- **The dendrite serves as an input channel to the neuron, while the axon serves as the output channel.**
- 树突作为神经元的输入通道,而轴突作为输出通道。
- **A neuron receives electrochemical inputs from other neurons at the dendrites.**
- 神经元在树突处接收来自其他神经元的电化学输入。
- **Suppose the sum of these inputs is sufficiently powerful to activate the neuron. In that case, it transmits an electrochemical signal through the axon to other neurons whose dendrites are connected to any of its axon terminals.**
- 假设这些输入的总和足够强大以激活神经元,那么它会通过轴突将电化学信号传递给树突连接到其任意轴突终端的其他神经元。
- **This connection among neurons is enabled via the synapses.**
- 神经元之间的这种连接通过突触实现。
- **The neuro-biological system is formidably connected. A typical cortical neuron has up to 10K inputs, and some cerebellar neurons have up to a quarter of a million inputs.**
- 神经生物系统具有极强的连接性。一个典型的皮质神经元有多达1万个输入,而一些小脑神经元有多达25万个输入。
- **Therefore, artificial neurons are designed to operate in a manner analogous to biological neurons.**
- 因此,人工神经元的设计操作方式类似于生物神经元。
- **Figure 1.1b shows a computational neuron model.**
- 图1.1b展示了一个计算神经元模型。
- **The input signals (e.g., x0) received from the axon of other neurons are multiplied with the weight of the synapse that connects them (e.g., w0).**
- 从其他神经元的轴突接收的输入信号(例如,x0)与连接它们的突触权重相乘(例如,w0)。
- **The dendrite then transports weighted inputs (e.g., w0x0) to the soma of the receiving neuron.**
- 树突然后将加权输入(例如,w0x0)传输到接收神经元的胞体。
- **The weighted inputs are summed up as the neuron membrane potential and passed through an activation function that maps it to the neuron’s output (Fig. 1.2).**
- 加权输入被汇总为神经元膜电位,并通过激活函数将其映射到神经元的输出(图1.2)。
- **Over the years, several neural network modeling approaches have been proposed, differing in topology and features, to capture the dynamics of neural computation.**
- 多年来,已经提出了几种不同拓扑和特征的神经网络建模方法,以捕捉神经计算的动态。
- 注释:拓扑指的是神经网络中神经元连接的结构和方式。
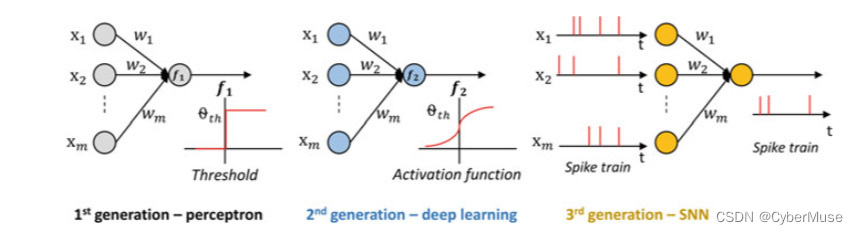
- **These modeling approaches have evolved through three generations, keeping in mind the computational principles of the biological brain.**
- 这些建模方法已经经过了三代演变,考虑了生物大脑的计算原理。
- **In the first generation, the neurons were referred to as perceptrons. These perceptrons process only digital signals using a single layer.**
- 第一代中,神经元被称为感知器。这些感知器仅使用单层处理数字信号。
- 注释:感知器是一种最简单的神经网络模型,用于二分类任务。
- **The sum of weighted inputs of this neuron is mapped to the neuron output using a binary threshold.**
- 该神经元的加权输入总和通过二值阈值映射到神经元的输出。
- **Some examples of perceptrons include Hopfield networks and Boltzmann machines.**
- 感知器的一些例子包括Hopfield网络和Boltzmann机。
- 注释:Hopfield网络是一种递归神经网络,Boltzmann机是一种随机生成模型。
- **The second generation, neurons, are called a conventional artificial neural network.**
- 第二代神经元被称为传统的人工神经网络。
- **It maps the sum of weighted inputs to the neuron output using activation functions such as sigmoid, exponential, and polynomial, which have a continuous set of possible outputs.**
- 它使用如Sigmoid、指数和多项式等激活函数将加权输入的总和映射到神经元的输出,这些函数具有连续的可能输出集。
- 注释:激活函数是用于引入非线性特性的函数,如Sigmoid函数将输入映射到0和1之间。
- **Also, this second-generation network employs learning algorithms based on gradient descent.**
- 此外,这一代网络使用基于梯度下降的学习算法。
- 注释:梯度下降是一种优化算法,用于最小化损失函数。
- **Examples of this generation of the neural network include Feedforward, radial basis function units, and recurrent sigmoid neural network.**
- 这一代神经网络的例子包括前馈网络、径向基函数单元和递归Sigmoid神经网络。
- 注释:前馈网络是最简单的神经网络形式,径向基函数单元用于分类任务,递归神经网络用于处理序列数据。
- **The third generation, referred to as the Spiking Neural Network (SNN), is modeled more analogous to the dynamics of biological neurons than previous generations.**
- 第三代称为脉冲神经网络(SNN),其建模更类似于生物神经元的动态。
- **It is event-driven and operates by accumulating input spikes at its membrane potential.**
- 它是事件驱动的,通过在膜电位处累积输入脉冲来运行。
- **An output spike is fired by the neuron only when its membrane potential exceeds a certain threshold.**
- 只有当膜电位超过某个阈值时,神经元才会发出输出脉冲。
- **To perform tasks, artificial neurons like their biological counterparts need to be connected.**
- 为了执行任务,人工神经元像它们的生物对应物一样需要连接。
- **The manner in which neurons are connected determines their topology.**
- 神经元连接的方式决定了它们的拓扑结构。
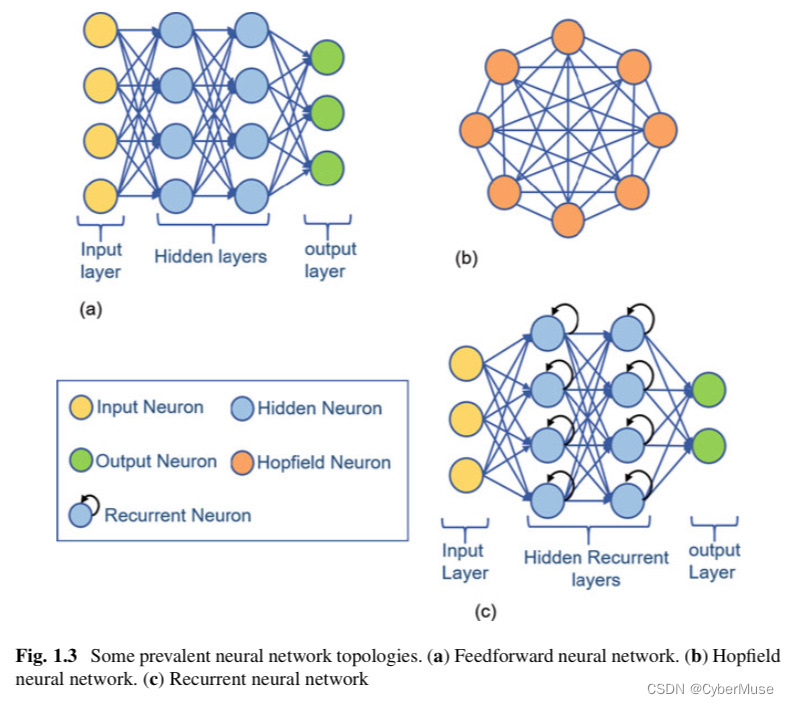
A summary of some neural network topologies illustrated in Fig. 1.3 are described as:
图1.3中展示了一些神经网络拓扑结构的摘要描述如下:
• Feed-forward neural networks (FFNN):
前馈神经网络(Feed-forward Neural Networks, FFNN):
This network topology described in Fig.1.3 is organized into three categories of layers: The input, hidden, and output layer.
这种网络拓扑结构分为输入层、隐藏层和输出层三类。*注释:输入层(Input Layer)、隐藏层(Hidden Layer)和输出层(Output Layer)是神经网络中的基本层次结构。*
The connections between neurons in this network are made across layers and not within a layer.
网络中的神经元连接是跨层进行的,而不是在层内进行。*注释:“跨层”指的是神经元连接从一个层延伸到另一个层,而不是在同一个层内。*
Information flows in a forward direction from the input layer, through the hidden layer(s), and finally to the output layer.
信息从输入层,经过隐藏层,最终到达输出层,沿着一个前向的方向流动。*注释:“前向”指的是信息流动的方向是单向的,没有反馈或环路。*
The backpropagation learning method is usually employed in training this network.
通常采用反向传播(Backpropagation)学习方法来训练这种网络。*注释:反向传播是一种用于调整神经网络权重的算法,通过计算输出误差的梯度来更新网络权重。*
The multilayer perceptron is another network with a similar topology as the feed-forward neural network.
多层感知器(Multilayer Perceptron, MLP)是另一种与前馈神经网络拓扑结构类似的网络。*注释:多层感知器是一种包含多个隐藏层的前馈神经网络。*
An example of a feed-forward neural network usually employed in pattern recognition and classification tasks is the radial basis function.
前馈神经网络的一个常见例子是径向基函数(Radial Basis Function, RBF)网络,通常用于模式识别和分类任务。*注释:径向基函数网络是一种基于距离的神经网络,用于函数逼近和分类。*
Hopfield neural network (HFs):
Hopfield神经网络(Hopfield Neural Networks, HFs):
This network topology possesses cyclic and recursive characteristics.
这种网络拓扑具有循环和递归特性。*注释:“循环和递归”指的是网络中存在反馈和自连接,使得节点之间可以形成环路。*
They are made up of binary threshold neurons with recurrent connections between them and can behave in several ways: settling in a stable state, oscillating, or following less predictable disorganized trajectories.
它们由具有递归连接的二值阈值神经元组成,并且可以以多种方式表现:稳定在一个稳定状态,振荡,或遵循不太可预测的无序轨迹。*注释:二值阈值神经元是指输出只有两个可能值(如0和1),递归连接是指神经元之间的相互连接形成环路。*
Its global energy is determined by summing up several contributions, and each contribution can also be determined from one symmetric connection between neurons and the binary states of the two neurons.
其全局能量通过汇总几个贡献来确定,每个贡献也可以从一个对称连接和两个神经元的二进制状态中确定。*注释:全局能量是指网络的总能量状态,由各个神经元之间的连接和状态决定。*
• Recurrent neural networks (RNNs):
递归神经网络(Recurrent Neural Networks, RNNs):
The recurrent neural network is derived from the FFNNs.
递归神经网络源自前馈神经网络(FFNNs)。*注释:递归神经网络是前馈神经网络的一个扩展,具有循环连接。*
However, as described in Fig. 1.3c, its hidden layers are replaced with recurrent layers.
然而,如图1.3c所述,其隐藏层被递归层所取代。*注释:递归层指的是能够接收自身输出作为输入的层。*
The layers of an RNN receive inputs from previous layers and the output of its layer.
RNNs的层接收来自前一层的输入以及其自身层的输出。*注释:这使得RNN能够处理序列数据,因为每个节点不仅依赖于当前输入,还依赖于之前的输出。*
The ability of RNNs to process sequences of inputs with their internal state makes them suitable for speech recognition and connected handwriting recognition.
RNNs处理输入序列及其内部状态的能力使其适合用于语音识别和连笔手写识别。*注释:序列数据处理能力是指RNN可以考虑输入数据的时间顺序和上下文。*
【注释】
### 神经网络拓扑结构总结
同学们,今天我将为大家总结和解释一些神经网络的基本拓扑结构。这些内容不仅是理论基础,也是实际应用的重要部分。我们将通过归纳和类比的方法来理解这些概念。为了更好地理解,我会在每个类别下举一些例子。
#### 1. 前馈神经网络(Feed-forward Neural Networks, FFNN)
**定义**
前馈神经网络是最基本的神经网络类型。它们由三种层次组成:输入层(Input Layer)、隐藏层(Hidden Layer)和输出层(Output Layer)。网络中的神经元连接是跨层进行的,而不是在同一层内。
**信息流动**
信息从输入层传递到隐藏层,然后到达输出层,整个过程是单向的,没有反馈环路。这种前向的流动方式使得网络结构相对简单。
**学习方法**
通常,前馈神经网络使用反向传播(Backpropagation)算法进行训练。反向传播通过计算输出误差的梯度来更新网络权重。
**例子**
- **多层感知器(Multilayer Perceptron, MLP)**
多层感知器是一种包含多个隐藏层的前馈神经网络,广泛应用于分类和回归任务。
- **径向基函数网络(Radial Basis Function, RBF)**
径向基函数网络是一种基于距离的前馈神经网络,通常用于模式识别和分类任务。
#### 2. Hopfield神经网络(Hopfield Neural Networks, HFs)
**定义**
Hopfield神经网络是一种具有循环和递归特性的网络。它们由二值阈值(Binary Threshold)神经元组成,这些神经元之间有递归连接。
**行为特性**
这种网络可以表现出多种行为:稳定在某个状态、振荡,或者遵循不太可预测的无序轨迹。其全局能量通过汇总各个连接的贡献来确定。
**例子**
- **记忆存储**
Hopfield网络常用于联想记忆系统,其中网络可以从部分或噪声输入恢复出完整的记忆。
#### 3. 递归神经网络(Recurrent Neural Networks, RNNs)
**定义**
递归神经网络是从前馈神经网络演变而来的,其隐藏层被递归层所取代。递归层可以接收来自前一层的输入和自身的输出。
**信息处理**
这种结构使得RNN能够处理序列数据,因为每个节点不仅依赖于当前输入,还依赖于之前的输出和状态。
**应用**
RNN在处理时间序列问题上表现出色,适用于语音识别和连笔手写识别等任务。
**例子**
- **语音识别**
在语音识别中,RNN可以处理连续的音频信号,识别出语音内容。
- **连笔手写识别**
RNN能够识别连笔手写字符,因为它可以处理连续的笔画输入。
### 神经元结构基础
为了帮助大家更好地理解神经网络,我们还需要了解一些神经元(Neuron)的基础结构:
- **轴突(Axon)**
神经元的轴突传递神经冲动到其他神经元。
- **突触(Synapse)**
突触是两个神经元之间进行信号传递的连接点。
- **树突(Dendrite)**
树突接收来自其他神经元的信号。
- **细胞核(Nucleus)**
神经元的细胞核控制细胞的基因活动。
- **轴突末端(Axon Terminals)**
轴突末端是神经冲动传递到下一个神经元的部位。
- **细胞体(Soma)**
细胞体包含神经元的细胞核,是信息处理的中心。
#### 3. 数学模型的基本要素
**输入信号(Input Signals)**
在数学模型中,输入信号可以类比于树突接收到的信号。这些信号通过突触传递到神经元。
**权重(Weights)**
每个输入信号都有一个权重,这可以类比于突触的强度。权重决定了输入信号对输出的影响大小。
**加权和(Weighted Sum)**
所有输入信号和权重的乘积之和称为加权和:
\[ S = \sum_{i=1}^{n} w_i \cdot x_i \]
其中,\( w_i \) 是第 \( i \) 个输入的权重,\( x_i \) 是第 \( i \) 个输入信号。
**激活函数(Activation Function)**
加权和通过激活函数,决定神经元的输出。这可以类比于神经元细胞体根据输入信号的强度决定是否发出信号。常见的激活函数有:
- **阶跃函数(Step Function)**
\[ f(x) = \begin{cases} 1 & \text{if } x \geq \theta \\ 0 & \text{if } x < \theta \end{cases} \]
- **Sigmoid函数(Sigmoid Function)**
\[ f(x) = \frac{1}{1 + e^{-x}} \]
- **ReLU函数(Rectified Linear Unit, ReLU)**
\[ f(x) = \max(0, x) \]
**输出(Output)**
激活函数的结果就是神经元的输出,这可以类比于轴突末端传递到下一个神经元的信号。
#### 4. 例子:感知器模型(Perceptron Model)
**感知器(Perceptron)**是最简单的神经网络模型之一。它由输入层和输出层组成,没有隐藏层。其数学模型如下:
\[ y = f\left( \sum_{i=1}^{n} w_i \cdot x_i + b \right) \]
其中,\( y \) 是输出,\( x_i \) 是输入,\( w_i \) 是权重,\( b \) 是偏置项,\( f \) 是激活函数。
**例子应用**
假设我们有一个简单的二分类问题,例如判断一个邮件是否是垃圾邮件。我们可以用感知器模型来进行分类:
- 输入层:邮件的特征(如是否包含特定关键词)。
- 权重:每个特征的重要性。
- 激活函数:决定邮件是否是垃圾邮件。
通过训练,我们可以调整权重和偏置,使模型能够准确分类。
【注释2】
### 硬件级别神经形态计算的实现
今天我们来讨论神经形态计算(Neuromorphic Computing)在硬件级别的实现。这项技术通过模拟生物神经网络的结构和功能,旨在实现高效的计算。下面我们将逐一介绍几种主要的实现技术:自旋电子存储器(Spintronic Memories)、阈值开关(Threshold Switches)、互补金属氧化物半导体晶体管(CMOS Transistors)和氧化物基忆阻器(Oxide-based Memristors)。
#### 1. 自旋电子存储器(Spintronic Memories)
**定义**
自旋电子存储器利用电子的自旋状态(Spin State)进行信息存储和处理。
**工作原理**
自旋电子技术依赖于控制和检测电子自旋的方向。通过磁性隧道结(Magnetic Tunnel Junction, MTJ),自旋电子存储器可以实现非易失性存储。
**优点**
- 高速读写
- 非易失性
- 高密度存储
**应用**
自旋转移力矩磁性随机存储器(Spin-Transfer Torque Magnetic Random Access Memory, STT-MRAM)在高速缓存和主存储器中有广泛应用。
**例子**
在神经形态计算中,自旋电子存储器可以用作神经元的权重存储单元,模拟突触的可塑性。
#### 2. 阈值开关(Threshold Switches)
**定义**
阈值开关是一种在特定电压下切换状态的电子元件。
**工作原理**
阈值开关在低于阈值电压时呈现高阻态,当电压超过阈值时迅速转变为低阻态。
**优点**
- 快速响应
- 低功耗
**应用**
阈值开关常用于实现神经元的激励功能,模拟神经元的“触发”行为。
**例子**
在神经形态计算中,阈值开关可以用来实现神经元的膜电位模型,当输入信号累积到一定程度时触发输出信号。
#### 3. 互补金属氧化物半导体晶体管(CMOS Transistors)
**定义**
CMOS晶体管是由互补的 n 型和 p 型金属氧化物半导体场效应晶体管(MOSFET)组成的集成电路。
**工作原理**
CMOS技术利用 n 型和 p 型晶体管的互补特性,实现低功耗、高速度的逻辑运算。当输入电压为高电平时,n型MOSFET导通,p型MOSFET截止,输出为低电平。反之,当输入电压为低电平时,p型MOSFET导通,n型MOSFET截止,输出为高电平。这样就实现了逻辑反转。
**优点**
- 低功耗
- 高集成度
- 高可靠性
**应用**
CMOS晶体管广泛应用于数字逻辑电路、模拟电路及混合信号电路中。
**例子**
在神经形态计算中,CMOS晶体管可以用来设计神经元电路和突触电路,实现计算和信号传输。
【补充】
1. **CMOS晶体管(CMOS Transistor)**
- 反相器(Inverter)
- 组成:n型MOSFET + p型MOSFET
- 工作原理:输入高电平 -> n型导通,p型截止 -> 输出低电平
- 低功耗(Low Power Consumption)
- 原理:静态不消耗电能
- 优势:适用于便携设备
- 高速度(High Speed)
- 原理:快速切换
- 优势:适用于高速运算
2. **具体应用(Specific Applications)**
- CMOS反相器(CMOS Inverter)
- 应用:数字电路基本单元
- 例子:CPU中的逻辑门
- CMOS NAND门(CMOS NAND Gate)
- 应用:构建复杂数字电路
- 例子:SRAM中的数据处理
- CMOS运算放大器(CMOS Operational Amplifier)
- 应用:模拟信号处理
- 例子:手机音频处理电路
#### 4. 氧化物基忆阻器(Oxide-based Memristors)
**定义**
忆阻器是一种具有可变电阻的非线性元件,其电阻值依赖于通过的电荷量。
**工作原理**
忆阻器的电阻状态可以通过施加电压改变,并且在电源关闭后保持其状态,具有记忆效应。
**优点**
- 非易失性
- 高密度
- 可模拟突触可塑性
**应用**
忆阻器常用于模拟生物突触的权重调整过程,适用于神经网络的硬件实现。
**例子**
在神经形态计算中,氧化物基忆阻器可以用作突触权重存储单元,模拟突触的可塑性和学习过程。
### 归纳总结
通过以上几种技术的介绍,我们可以归纳出神经形态计算的实现路径:
1. **自旋电子存储器**主要用于高速、非易失性存储,适用于模拟突触权重。
2. **阈值开关**用于实现神经元的触发行为,模拟神经元的膜电位变化。
3. **CMOS晶体管**为神经形态计算提供了高效的逻辑和模拟电路设计平台。
4. **氧化物基忆阻器**通过其可变电阻特性,模拟生物突触的学习和记忆功能。
希望这些解释和示例能帮助大家更好地理解神经形态计算在硬件级别的实现。如果有任何问题,欢迎随时提问!