一、 单相整流电路

任务：把正弦电压转变为单向脉动的电压。

类型：有单相半波、全波、桥式和倍压整流等。

分析方法：为分析简单起见，把二极管当作理想元件处理，即二极管的正向导通电阻为零，反向电阻为无穷大。

1、半波整流电路

设$u_2=\sqrt{2}{U}_{2}sin(\omega t)$，$u_2$有效值为$U_2$。

当$u_2>0$，D ON，$u_L=u_2$；

当$u_2<0$，D OFF，$u_L=0$。

故就是把交流电压$u_2$中负值全部去掉，只留下正值。

此时流过电阻的输出电压和输出电流是多少？

（1）输出电压平均值$U_L$

根据上述$u_2$的方程和$u_L$的变化图形通过积分求解。

$U_L=\frac{1}{2\pi }{\int }_0^{\pi }{u}_{2}d(\omega t)+0=\frac{1}{2\pi }{\int }_0^{\pi }\sqrt{2}{U}_{2}sin(\omega t)d(\omega t)=-\frac{\sqrt{2}}{2\pi }{U}_{2}cos(\omega t){|}_0^{\pi }=\frac{\sqrt{2}}{\pi }{U}_2\approx 0.45U_2$

（2）输出电流平均值$I_L$

$I_L=\frac{U_L}{R_L}=0.45U_2/R_L$

（3）流过二极管的平均电流$I_D$

$I_D=I_L$

（4）二极管承受的最高反向电压$U_{RM}$

二极管承受的最高反向电压就是电压取最值。

当$u_2>0$，$u_L=u_2$；

当$u_2<0$，$u_L=0$。

所以，$U_{RM}=\sqrt{2}{U}_2$

---

半波整流电路中，交流电路只有一半能起到作用，我们希望能把电压为负数的部分也利用起来，最好是把它翻到正值部分，而不是直接滤掉，于是有了全波整流电路。

2、全波整流电路

原理： 变压器副边中心抽头，感应出两个相等的电压u2

设$u_2=\sqrt{2}{U}_{2}sin(\omega t)$，$u_2$有效值为$U_2$。

当$u_2>0$，D1 ON，D2 OFF，$u_L=u_2$；

当$u_2<0$，D1 OFF，D2 ON，$u_L=-u_2$。

（1）输出电压平均值$U_L$

根据上述$u_2$的方程和$u_L$的变化图形通过积分求解。

此时$u_L$的周期变为$\pi$。

$U_L=\frac{1}{\pi }{\int }_0^{\pi }{u}_{2}d(\omega t)=\frac{1}{\pi }{\int }_0^{\pi }\sqrt{2}{U}_{2}sin(\omega t)d(\omega t)=-\frac{\sqrt{2}}{\pi }{U}_{2}cos(\omega t){|}_0^{\pi }=\frac{2\sqrt{2}}{\pi }{U}_2\approx 0.9U_2$

（2）输出电流平均值$I_L$

$I_L=\frac{U_L}{R_L}=0.9U_2/R_L$

（3）流过二极管的平均电流$I_D$

此时每个二极管轮流为电阻供电，在一半的周期里，$i_D=i_L$，在另一半里，$i_D=0$，故为$I_L$的一半。

$I_D=I_L/2$

（4）二极管承受的最高反向电压$U_{RM}$

二极管承受的最高反向电压就是2倍电压取最值。$U_{RM}=2\sqrt{2}{U}_2$

用KVL求解：

以D1为例，当D1 ON，$u_{D1}=0$；当D1 OFF，$u_2+u_L-u_{D1}=0$=>$u_{D1}=2u_2$

---

当电压很大时，用线圈来整流会很累赘，所以需要更加好的方式来实现整流。

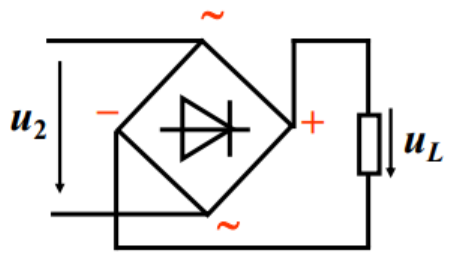
3、桥式整流电路

（1）组成：由四个二极管组成桥路

（2）工作原理

当$u_2>0$，D1、D3 ON，D2、D4 OFF，$u_L=u_2$；

当$u_2<0$，D1、D3 OFF，D2、D4 ON，$u_L=-u_2$。

（3）主要参数：

输出电压平均值：$U_L=0.9U_2$

输出电流平均值:$I_L=\frac{U_L}{R_L}=0.9U_2/R_L$

流过二极管的平均电流：$I_D=I_L/2$

二极管承受的最大反向电压：$U_{RM}=\sqrt{2}{U}_2$ （这个从图中分析可知，当D OFF时，其两端连的就是电压$u_2$）

交直流管脚*

上下接电源；左右接内阻

二、滤波电路

1.电容滤波

（1）空载（$R_L$=∞）时：

$u_3>u_c$时，D导通，C充电

$u_3<u_c$时，D截止，C放电，但是因为$R_L$=∞，C无法放电，$u_c$保持。

（2）接入$R_L$（且$R_L$C较大）时

$u_3>u_c$时，D导通，C充电

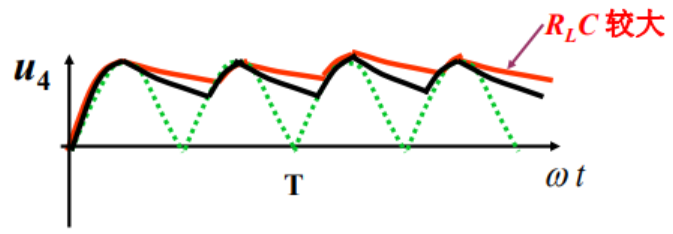
$u_3<u_c$时，D截止，C通过$R_L$放电，$u_c$减小，因为$R_L$C大，所以放电会久，没有放完之前就会被再次充满。

如图，$u_c$变平滑。

（3）电容滤波的效果

时间常数$\tau =R_{L}C$越大，电容放电需要时间越久，滤波效果越好。

${\mathbb{R}}_{L}C$ 愈大→ C放电越慢→ 输出电压越平稳→ 脉动成分越小→ 负载平均电压越大

一般取$\tau ={\mathbb{R}}_{L}C\ge (3\backsim 5)\frac{2}{T}$

此时的==$U_C\approx 1.2U_2$==，大于原来的$0.9U_2$

2.电感滤波电路

电路结构: 在桥式整流电路与负载间串入一电感L。

电感：通直流，阻交流

对直流分量: $X_L=0$ 相当于短路,电压大部分降在$R_L$ 上

对谐波分量: f 越高，$X_L$ 越大,电压大部分降在电感上。 因此，在输出端得到比较平滑的直流电压。

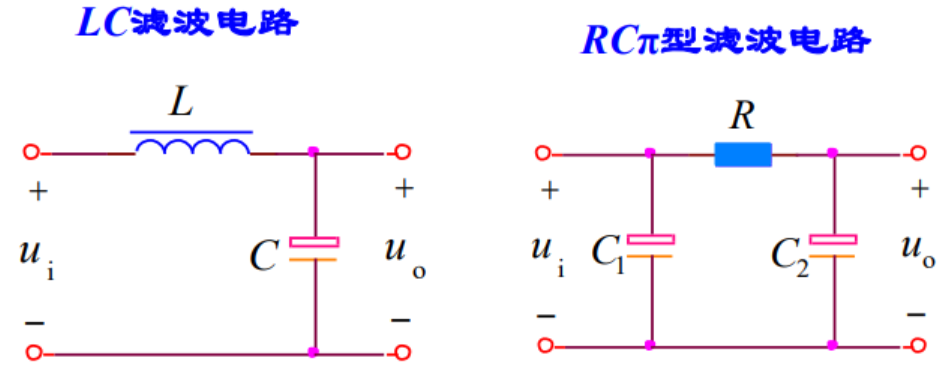
3.其它滤波电路

为进一步改善滤波特性，可将上述滤波电路组合起来使用。