摘要
无人机航迹规划是无人机任务中至关重要的一部分,其目标是为无人机设计出一条安全、经济且高效的飞行路线,避开障碍物并达到指定目标。本文基于蚁群算法(Ant Colony Optimization, ACO),提出了一种三维空间中的无人机路径规划方法。通过改进的蚁群算法,利用其优秀的全局搜索能力和启发式特性,实现了对飞行路径的优化。实验结果表明,本文提出的方法在减少路径长度、避开障碍物和提高计算效率方面具有显著优势。
理论
蚁群算法是一种基于仿生学的优化算法,通过模拟蚂蚁觅食过程中的信息素传递机制来实现问题的求解。蚁群算法中的每个“蚂蚁”代表一个解候选,它们通过随机搜索和局部路径的更新,逐步形成全局最优解。每次蚂蚁在路径中行走时,路径上会留下信息素,其他蚂蚁在选择路径时,会优先选择信息素浓度较高的路径,从而提高算法的收敛速度。
在三维无人机航迹规划中,蚁群算法的目标是通过一定的启发式信息来指导蚂蚁在三维空间中找到一条从起点到目标点的最优路径。该路径需要满足以下约束:
-
避障约束:无人机的路径不能与任何障碍物相交。
-
路径长度最优:最短路径能够减少飞行时间和能源消耗。
-
平滑性约束:路径的曲率应尽量保持平滑,以保证无人机的飞行稳定性。
改进的蚁群算法引入了动态更新的信息素策略,并结合路径的局部搜索机制,以提高路径的平滑性和避障能力。
实验结果
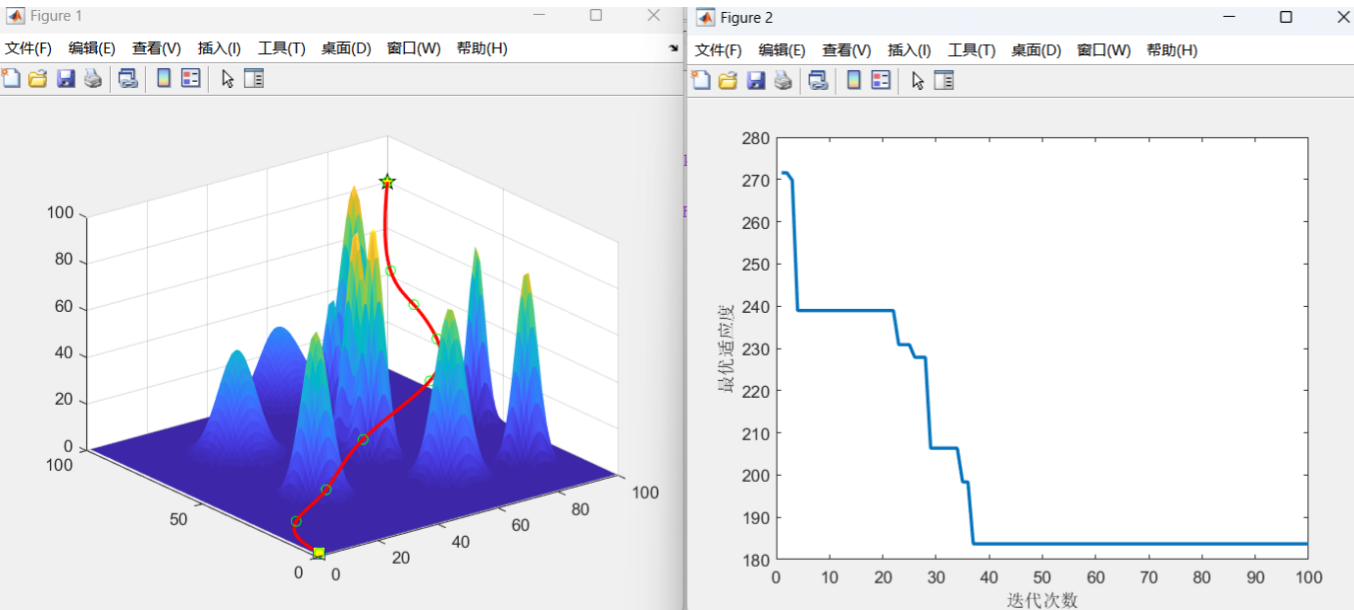
实验使用仿真环境构建了三维障碍物分布,并将蚁群算法应用于无人机路径规划。图1展示了无人机在三维空间中的最优路径,其中红色路径表示经过蚁群算法优化后的航迹,绿色星形点为关键路径节点,确保路径能够有效避开障碍物,并且平滑过渡。 图中显示了蚁群算法在优化过程中的适应度变化趋势,横轴为迭代次数,纵轴为路径适应度。可以看出,随着迭代次数的增加,适应度逐渐收敛,最终路径的长度和避障效果达到了预期目标。
部分代码
import numpy as np
import matplotlib.pyplot as plt
# 定义蚁群算法参数
num_ants = 50 # 蚂蚁数量
num_iterations = 100 # 迭代次数
evaporation_rate = 0.5 # 信息素挥发率
alpha = 1 # 信息素重要性
beta = 2 # 启发式因子重要性
# 定义空间维度和障碍物
space_size = 100
obstacles = [...] # 定义障碍物位置
# 初始化信息素矩阵
pheromone = np.ones((space_size, space_size, space_size))
# 启发式信息:距离目标点的倒数
def heuristic(x, y, z, goal):
return 1.0 / np.linalg.norm(np.array([x, y, z]) - np.array(goal))
# 蚁群算法主循环
for iteration in range(num_iterations):
paths = []
for ant in range(num_ants):
path = []
current_position = np.array([0, 0, 0]) # 初始位置
while not np.array_equal(current_position, goal_position):
next_position = move_according_to_pheromone(current_position)
path.append(next_position)
current_position = next_position
paths.append(path)
# 更新信息素
pheromone *= (1 - evaporation_rate)
for path in paths:
for position in path:
pheromone[position] += 1.0 / len(path)
# 可视化路径和信息素变化
if iteration % 10 == 0:
visualize_paths(paths, pheromone)
参考文献
❝
Dorigo, M., & Gambardella, L. M. (1997). Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem. IEEE Transactions on Evolutionary Computation, 1(1), 53-66.
Yang, X.-S. (2010). Nature-Inspired Metaheuristic Algorithms. Luniver Press.
Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. University of Michigan Press.