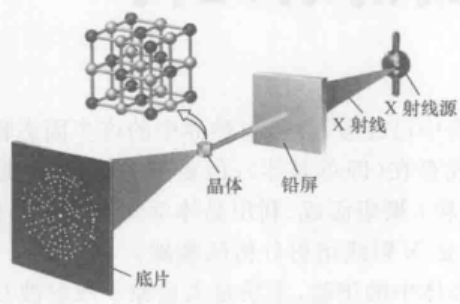
X射线在晶体中的衍射,实质是大量原子散射波互相干涉的结果。
衍射花样有两个特征:
-
衍射方向(衍射线在空间的分布规律):由晶胞的大小、形状和位向决定。
-
衍射强度:由原子的种类以及它在晶胞中所处的位置决定。
故衍射花样是晶体内部原子分布规律的反映。X射线衍射现象和实际晶体结构之间存在定性和定量的关系。
一、X射线的衍射现象
光的衍射:光在传播过程中,遇到障碍物或小孔时,光将偏离直线传播的路径而绕到障碍物后面传播的现象,此时波长与小孔或者光栅常数为同一数量级
为了证实X射线的本质以及原子排列的周期性假设,劳厄设置实验:用连续的X射线照射一个单晶体,并在晶体前方获得预期的X射线晶体衍射花样。
劳厄实验证实了两点: 1)晶体中原子排列具有周期性; 2)X射线本质就是电磁波
二、X射线衍射的方向(Direction)
1.劳厄方程
假设:
- 原子不做热振动,原子间距不变,按照空间点阵排列,无缺陷
- 原子中的电子集中在原子中心,忽略因为电子位置不同导致散射波的相位差
- 入射X射线互相平行,波长相等
(1)一维衍射(原子列)
根据衍射原理,散射线相长的前提是波程差是波长的整数倍。
下图中, A 1 A_1 A1, A 2 A_2 A2是相邻阵点,点阵常数为a,X射线波长为λ。
则波程差近似等于从 A 1 A_1 A1做垂线, A 2 A_2 A2做垂线得到的: A 1 H 2 − A 2 H 1 = a ( c o s α − c o s α 0 ) A_1H_2-A_2H_1=a(cos\alpha-cos\alpha_0) A1H2−A2H1=a(cosα−cosα0)
则得到劳厄第一方程(一维的劳厄方程)为: a ( c o s α − c o s α 0 ) = H λ a(cos\alpha-cos\alpha_0)=H\lambda a(cosα−cosα0)=Hλ,H为整数,称为劳厄第一干涉指数。
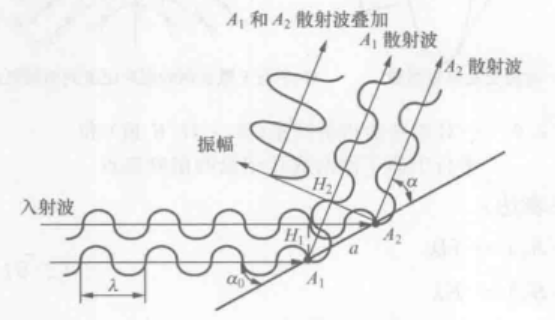
H可以取0,±1,……,不能一直取下去,因为 a ( c o s α − c o s α 0 ) a(cos\alpha-cos\alpha_0) a(cosα−cosα0)显然是有限的,最多可以取到[-2a,2a],所以H也是有限的。
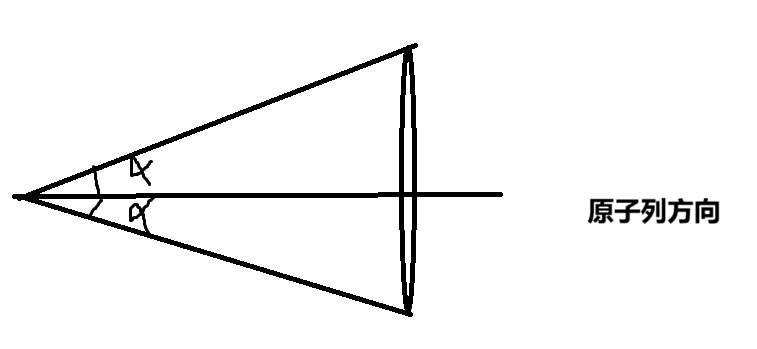
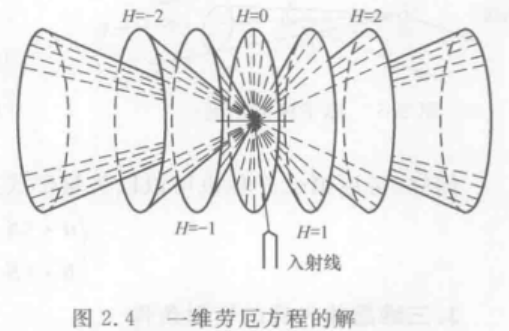
一维劳厄方程的解是一系列同轴不同张角的衍射圆锥簇。
解释:对于某一个方向的入射光以及取某一特定整数的H来说, α \alpha α取特定解,在空间中就代表和原子列的夹角为α的所有线,故成一个锥形那个,锥面的顶角为2α
矢量形式:入射方向用单位矢量 S 0 \bold S_0 S0表示,散射方向用单位矢量 S \bold S S表示, a ⋅ ( S − S 0 ) = H λ \bold a\cdot(\bold S-\bold S_0)=H\lambda a⋅(S−S0)=Hλ
(2)二维衍射(原子网)
原子网视为一系列平行的原子列组成。
X射线照到原子网时,每个原子列的衍射线均分布在自身的同轴圆锥簇上。每个圆锥簇用一个圆锥表示。

根据衍射原理,散射线相长的前提是波程差是波长的整数倍。
求 O 1 O1 O1和 O ′ 1 ′ O'1' O′1′的光程差, b ( c o s β − c o s β 0 ) b(cos\beta-cos\beta_0) b(cosβ−cosβ0)
则得到劳厄第二方程为: b ( c o s β − c o s β 0 ) = K λ b(cos\beta-cos\beta_0)=K\lambda b(cosβ−cosβ0)=Kλ,K为整数,称为劳厄第二干涉指数。
当X射线射到原子网时要发生衍射,必须同时满足劳厄第一、第二方程:
{
a
(
c
o
s
α
−
c
o
s
α
0
)
=
H
λ
b
(
c
o
s
β
−
c
o
s
β
0
)
=
K
λ
\left\{ \begin{array}{ll} a(cos\alpha-cos\alpha_0)=H\lambda\\ b(cos\beta-cos\beta_0)=K\lambda \end{array} \right.
{a(cosα−cosα0)=Hλb(cosβ−cosβ0)=Kλ
矢量形式:
{
a
(
S
−
S
0
)
=
H
λ
b
(
S
−
S
0
)
=
K
λ
\left\{ \begin{array}{ll} \bold a(\bold S-\bold S _0)=H\lambda\\ \bold b(\bold S-\bold S_0)=K\lambda \end{array} \right.
{a(S−S0)=Hλb(S−S0)=Kλ
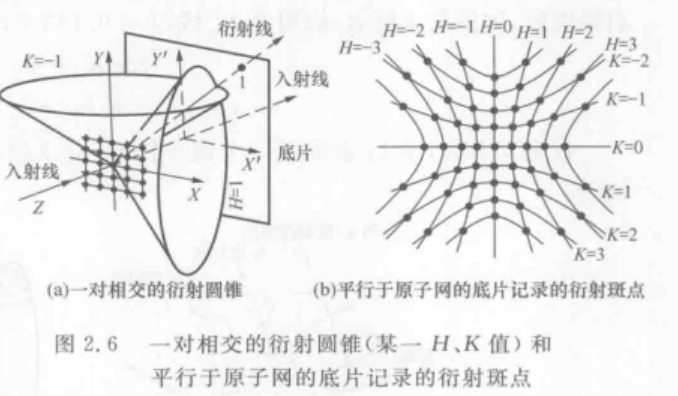
在几何上表现为,衍射线只能出现在沿X方向以及Y方向的两系列圆锥簇的交线或公共切线上。
在底片上,所有衍射圆锥给出的迹线为双曲线。每对双曲线的交点为衍射斑点。
(3)三维晶体光栅的衍射条件
三维空间点阵看作一系列平行的原子网组成。
X射线照射到三维晶体光栅后相互干涉能保留下来的衍射线,必然满足劳厄第三方程:
{
a
(
c
o
s
α
−
c
o
s
α
0
)
=
H
λ
b
(
c
o
s
β
−
c
o
s
β
0
)
=
K
λ
c
(
c
o
s
γ
−
c
o
s
γ
0
)
=
L
λ
\left\{ \begin{array}{ll} a(cos\alpha-cos\alpha_0)=H\lambda\\ b(cos\beta-cos\beta_0)=K\lambda\\ c(cos\gamma-cos\gamma_0)=L\lambda \end{array} \right.
⎩
⎨
⎧a(cosα−cosα0)=Hλb(cosβ−cosβ0)=Kλc(cosγ−cosγ0)=Lλ
L为整数,称为劳厄第三干涉指数,取值和H相似。
矢量形式:
{
a
(
S
−
S
0
)
=
H
λ
b
(
S
−
S
0
)
=
K
λ
c
(
S
−
S
0
)
=
L
λ
\left\{ \begin{array}{ll} \bold a(\bold S-\bold S _0)=H\lambda\\ \bold b(\bold S-\bold S_0)=K\lambda\\ \bold c(\bold S-\bold S_0)=L\lambda \end{array} \right.
⎩
⎨
⎧a(S−S0)=Hλb(S−S0)=Kλc(S−S0)=Lλ
就是在前面劳厄第二方程的基础上又加了一个维度而已。
几何上,衍射线只能出现在沿X、Y、Z方向三系列圆锥簇的相交处。
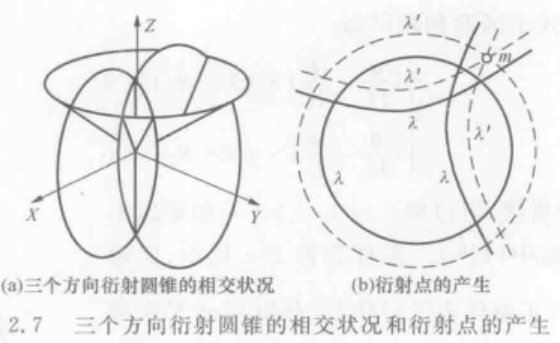
劳厄方程解决了X射线衍射方向问题,相长产生衍射的条件是晶体三个重复周期上的相邻原子散射线所在方向上光程差同时为波长的整数倍。
描述这个三维衍射圆锥所需参数:衍射线和三个基本方向夹角为α、β、γ,取决于晶体点阵周期a、b、c,入射X射线和三个基本方向的夹角为 α 0 、 β 0 、 γ 0 \alpha_0、\beta_0、\gamma_0 α0、β0、γ0,X射线的波长λ以及干涉指数HKL
三维的衍射圆锥难以表示想象,需要简化。
2.布拉格方程(Bragg’s Law)
在三维劳厄方程基础上:
{
a
H
(
S
−
S
0
)
=
λ
b
K
(
S
−
S
0
)
=
λ
c
L
(
S
−
S
0
)
=
λ
=
>
{
(
a
H
−
b
K
)
⋅
(
S
−
S
0
)
=
0
(
b
K
−
c
L
)
⋅
(
S
−
S
0
)
=
0
\left\{ \begin{array}{ll} \frac{\bold a}H(\bold S-\bold S _0)=\lambda\\ \frac{\bold b}K(\bold S-\bold S _0)=\lambda\\ \frac{\bold c}L(\bold S-\bold S _0)=\lambda \end{array} \right. => \left\{ \begin{array}{ll} (\frac{\bold a}H-\frac{\bold b}K)\cdot(\bold S-\bold S _0)=0\\ (\frac{\bold b}K-\frac{\bold c}L)\cdot(\bold S-\bold S _0)=0 \end{array} \right.
⎩
⎨
⎧Ha(S−S0)=λKb(S−S0)=λLc(S−S0)=λ=>{(Ha−Kb)⋅(S−S0)=0(Kb−Lc)⋅(S−S0)=0
其中,HKL为干涉指数,绘制晶面如下:

晶面(HKL)和三个坐标轴交点为( a H , b K , c L \frac {\bold a}H,\frac{\bold b}K,\frac{\bold c}L Ha,Kb,Lc),所以 ( a H − b K ) (\frac{\bold a}H-\frac{\bold b}K) (Ha−Kb)和 ( b K − c L ) (\frac{\bold b}K-\frac{\bold c}L) (Kb−Lc)正好是图中带箭头的两个向量。
从上述式子推导发现矢量 ( S − S 0 ) (\bold S-\bold S _0) (S−S0)垂直于(HKL)晶面两个不平行的向量,也就是垂直于(HKL)晶面。则单位矢量 S \bold S S和 S 0 \bold S _0 S0如同镜面反射分布在(HKL)晶面上。
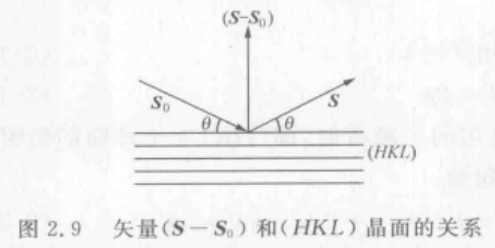
可以将晶体的衍射现象看作是晶体某些晶面“镜面反射”的结果。θ为入射角。
a ( S − S 0 ) / λ = H \bold a(\bold S-\bold S _0)/\lambda=H a(S−S0)/λ=H
根据倒易点阵基矢和正点阵基矢关系,得: ( S − S 0 ) / λ = H a ∗ (\bold S-\bold S _0)/\lambda=H\bold a^* (S−S0)/λ=Ha∗
令散射(衍射)波矢 k = S / λ \mathbf{k}=\mathbf{S}/\lambda k=S/λ,入射波矢 k 0 = S 0 / λ \mathbf{k_0}=\mathbf{S_0}/\lambda k0=S0/λ,上式变为: k − k 0 = H a ∗ = K \mathbf{k}-\mathbf{k_0}=H\mathbf{a^*}=\mathbf{K} k−k0=Ha∗=K
K \mathbf{K} K表示散射(衍射)波矢和入射波矢的差,要产生衍射则满足三维劳厄定律: K = H a ∗ + K b ∗ + L c ∗ \mathbf{K}=H\mathbf{a}^*+K\mathbf{b}^*+L\mathbf{c}^* K=Ha∗+Kb∗+Lc∗,所以 K \mathbf{K} K是倒易空间矢量,(HKL)是晶面指数。当波矢的差指向倒易点阵阵点时,满足三维劳厄方程,产生衍射: ( S − S 0 ) / λ = H a ∗ + K b ∗ + L c ∗ (\bold S-\bold S _0)/\lambda=H\mathbf{a}^*+K\mathbf{b}^*+L\mathbf{c}^* (S−S0)/λ=Ha∗+Kb∗+Lc∗,得到衍射条件的矢量方程。
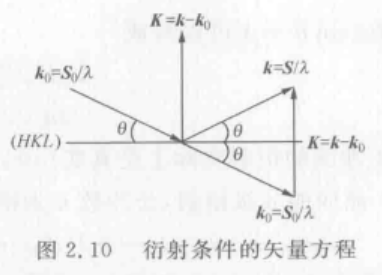
由图中几何关系: ∣ K ∣ = 1 d h k l = S s i n θ / λ + S 0 s i n θ / λ = 2 s i n θ / λ |\mathbf{K}|=\frac1{d_{hkl}}=\mathbf{S}sin\theta/\lambda +\mathbf{S_0}sin\theta/\lambda=2sin\theta/\lambda ∣K∣=dhkl1=Ssinθ/λ+S0sinθ/λ=2sinθ/λ
整理得到布拉格方程: 2 d s i n θ = λ 2dsin\theta=\lambda 2dsinθ=λ
引申:待测晶体的最小面间距大于等于光源的半波长
s i n θ = λ 2 d ≤ 1 sin\theta=\frac{\lambda}{2d}\leq 1 sinθ=2dλ≤1=> d H K L ≥ λ / 2 d_{HKL}\geq \lambda/2 dHKL≥λ/2
采用短波X射线作光源时,能测出的最小面间距就变小了,能获得更多的信息。
3.厄瓦尔德反射球(Ewald’s Sphere)
厄瓦尔德球是倒易空间的一种几何表示方法,是劳厄方程和布拉格方程的几何表达。
厄瓦尔德将布拉格方程2dsinθ=λ 改写为: s i n θ = 1 d / 2 λ sin\theta=\frac1d/\frac2{\lambda} sinθ=d1/λ2,并用作图的方式表达了这个方程和赋予其中一些项以新的含义。
反射球:以 1 λ \frac1{\lambda} λ1为半径,C为圆心做球。
球面经过被照射晶体的倒易原点 O ∗ O^* O∗,X射线入射方向矢量为 C O ∗ = S 0 / λ \mathbf{CO^*}=\mathbf{S_0}/\lambda CO∗=S0/λ,根据布拉格方程 s i n θ = 1 d / 2 λ sin\theta=\frac1d/\frac2{\lambda} sinθ=d1/λ2, 2 λ \frac2{\lambda} λ2是直径长度, 1 d \frac1d d1是倒易矢量的长度,θ是入射光/衍射光和衍射面的夹角,倒易点落在倒易球面上,衍射线的方向为从反射球球心C指向倒易点,入射矢量和衍射矢量夹角为2θ。
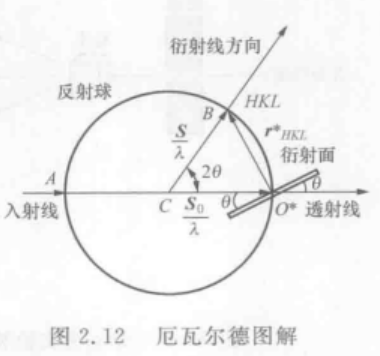
入射矢量: C O ∗ = S 0 / λ \mathbf{CO^*}=\mathbf{S_0}/\lambda CO∗=S0/λ
衍射矢量: C B = S / λ \mathbf{CB}=\mathbf{S}/\lambda CB=S/λ
倒易矢量: ∣ O ∗ B ∣ = 1 d |\mathbf{O^*B}|=\frac1d ∣O∗B∣=d1, O ∗ B ⊥ 衍射面 \mathbf{O^*B}\perp 衍射面 O∗B⊥衍射面
C B − C O ∗ = O ∗ B \mathbf{CB}-\mathbf{CO^*}=\mathbf{O^*B} CB−CO∗=O∗B
X射线波长越小,反射球半径越大,则倒易点越多,发生衍射的晶面越多,获得多级晶面衍射机会越多。