目录
- 二叉树进阶oj题
- 1.根据二叉树创建字符串
- 2.二叉树的层序遍历
- 3.二叉树的层序遍历 II
- 4.二叉树的最近公共祖先
- 5.二叉搜索树和双向链表
- 6.从前序与中序遍历序列构造二叉树
- 7.从中序和后序遍历序列来构造二叉树
- 8.二叉树的前序遍历,非递归迭代实现
- 9.二叉树中序遍历 ,非递归迭代实现
- 10.二叉树的后序遍历 ,非递归迭代实现
二叉树进阶oj题
1.根据二叉树创建字符串
根据二叉树创建字符串:
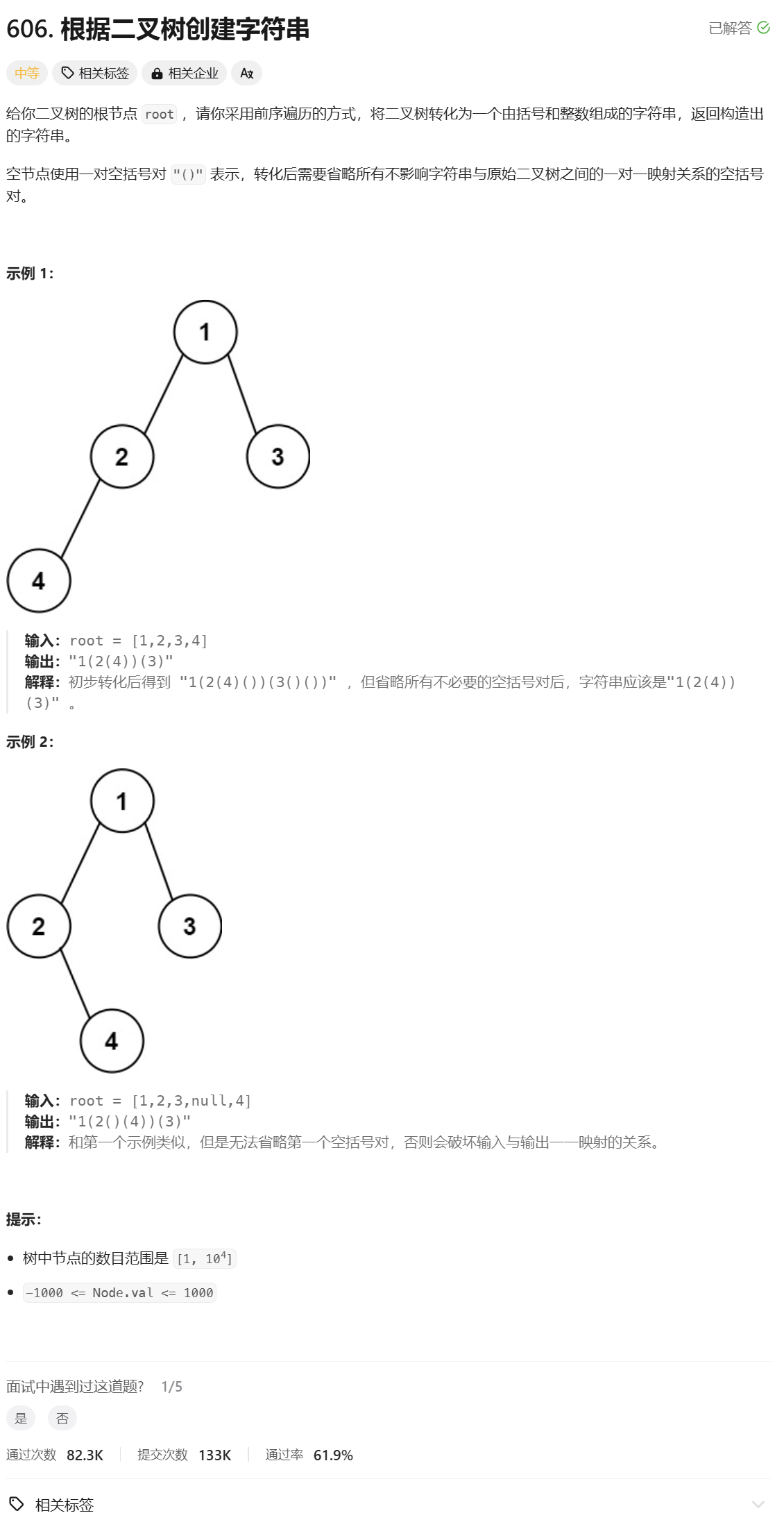
分析:

先递归左子树,再递归右子树,每递归到一个节点就套娃一个()。
要注意,当一个根节点的左孩子不存在右孩子存在时,要用一个()表示左孩子
class Solution {
public:
string tree2str(TreeNode* root)
{
// str作为最后的输出的字符串
string str;
// 要求前序遍历——根,左子树,右子树
str += to_string(root->val);
// 这里要分类讨论:
//1.左不为空
//2.左空,右不为空 这个情况要保留一个左的括号
if (root->left)
{
str += "(";
str += tree2str(root->left);
str += ")";
}
else if (root->right)
{
str += "()";
}
if (root->right)
{
str += "(";
str += tree2str(root->right);
str += ")";
}
return str;
}
};
2.二叉树的层序遍历
二叉树的层序遍历
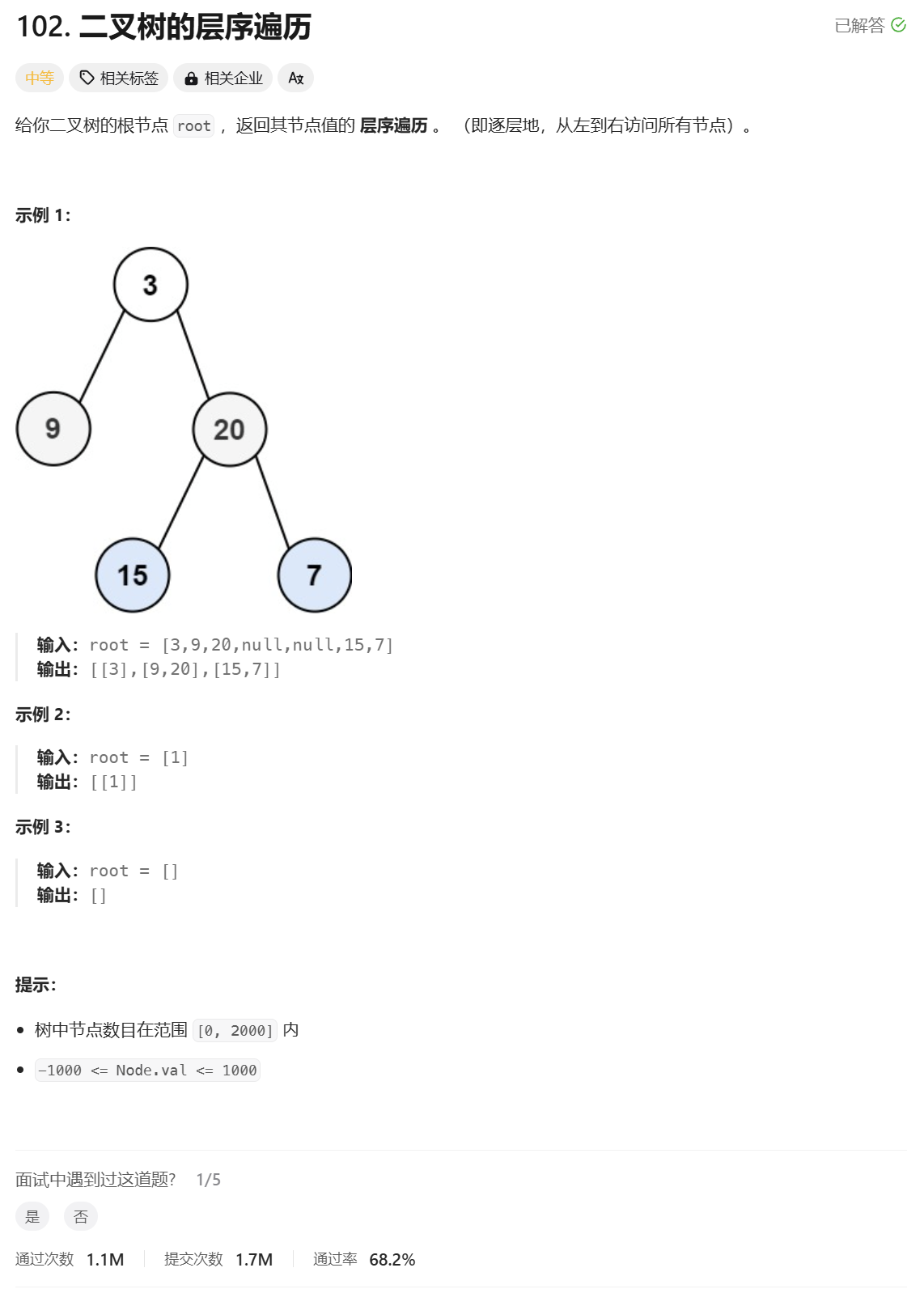
分析:
层序遍历就采用一个队列就可以实现。一个节点出来要记得带它的做右子树进节点
代码如下:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
vector<vector<int>> vv;
queue<TreeNode*> _q; // 通过队列实现层序
// 传空树进行不需要遍历了。
if (root)
_q.push(root);
while (!_q.empty())
{
// 通过控制每层的数据个数,来达到精确的输出二叉树每层的数据
// 意思就是 当第n层数据出完之后,第n+1层的数据个数就是此时的q.size()
int levelSize = _q.size();
vector<int> v;
for (size_t i = 0; i < levelSize; i++)
{
TreeNode* front = _q.front();
_q.pop();
v.push_back(front->val);
// 弹出节点后要带该节点的左右孩子
if (front->left)
_q.push(front->left);
if (front->right)
_q.push(front->right);
}
// 此时v就是装好了一层的数据,将其尾插到vv中
vv.push_back(v);
}
return vv;
}
};
3.二叉树的层序遍历 II
二叉树的层序遍历 II:
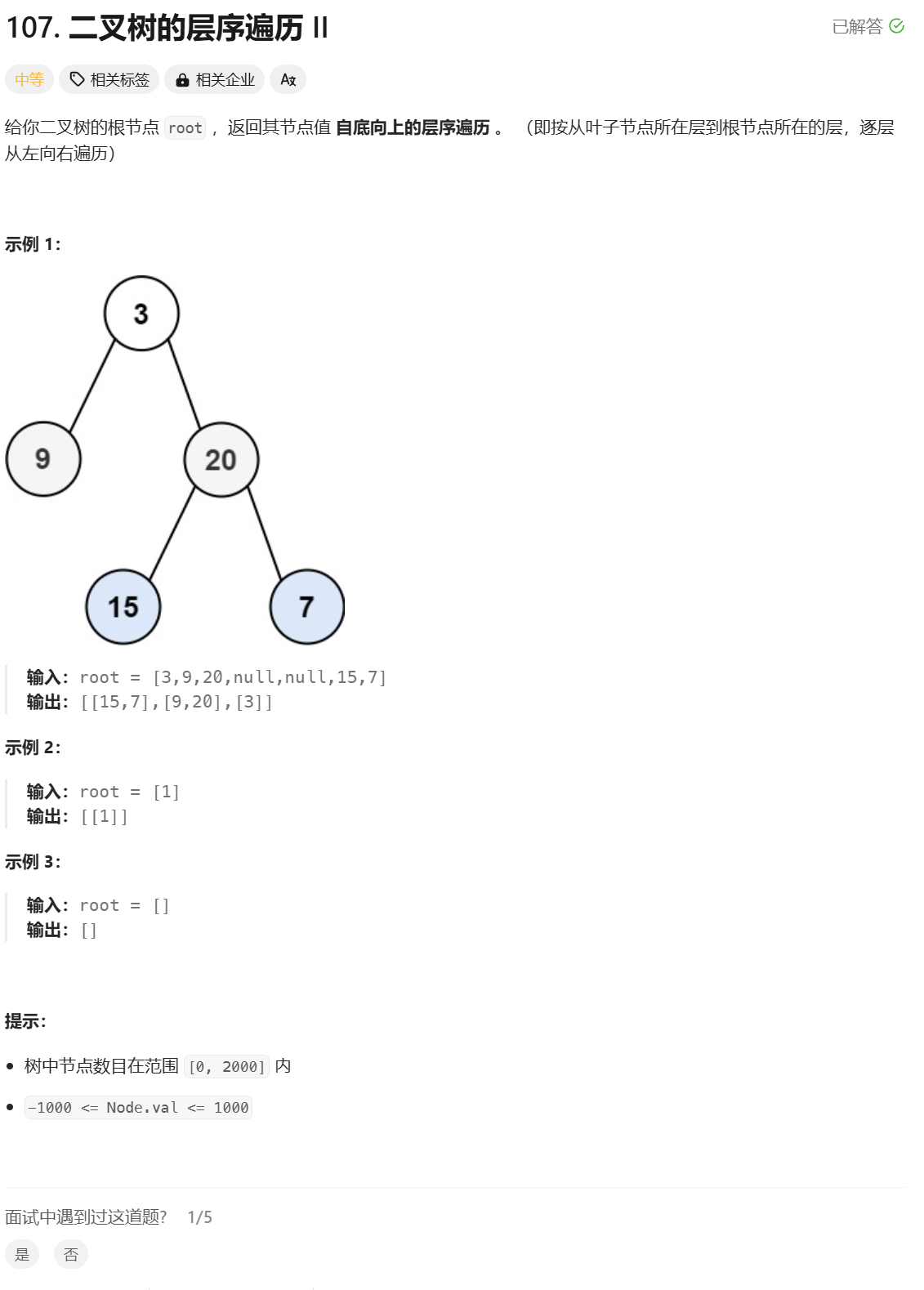
分析:
这道题和第2道题的思路是一样的,只需要将最后的结果逆置,也就是vv逆置一下,再输出就是自下而上的层序遍历
代码如下:
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root)
{
vector<vector<int>> vv;
queue<TreeNode*> _q; // 通过队列实现层序
// 传空树进行不需要遍历了。
if (root)
_q.push(root);
while (!_q.empty())
{
// 通过控制每层的数据个数,来达到精确的输出二叉树每层的数据
// 意思就是 当第n层数据出完之后,第n+1层的数据个数就是此时的q.size()
int levelSize = _q.size();
vector<int> v;
for (size_t i = 0; i < levelSize; i++)
{
TreeNode* front = _q.front();
_q.pop();
v.push_back(front->val);
// 弹出节点后要带该节点的左右孩子
if (front->left)
_q.push(front->left);
if (front->right)
_q.push(front->right);
}
// 此时v就是装好了一层的数据,将其尾插到vv中
vv.push_back(v);
}
// 只要逆置一下,就是自底向上的层序遍历
reverse(vv.begin(), vv.end());
return vv;
}
};
4.二叉树的最近公共祖先
二叉树的最近公共祖先
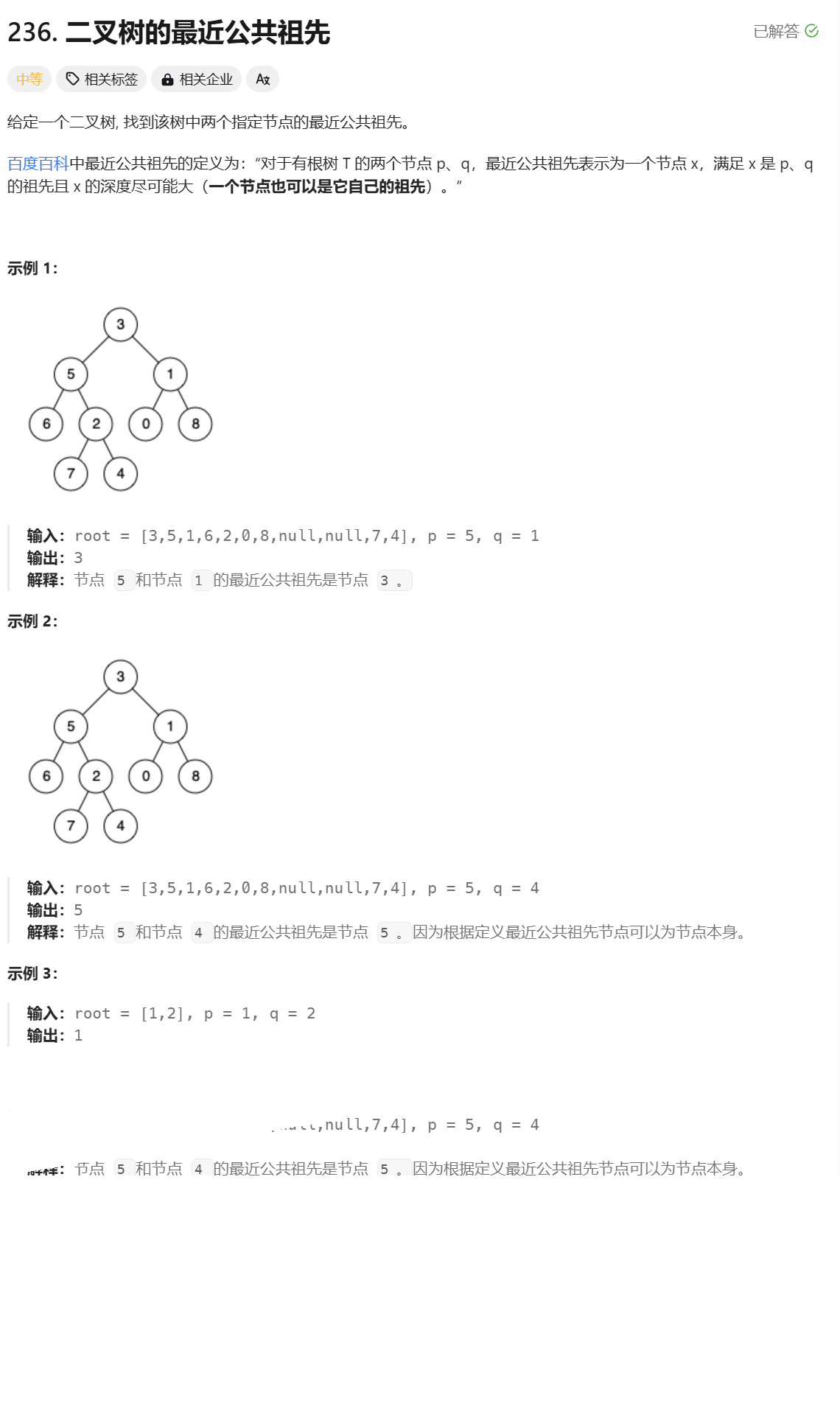
分析:
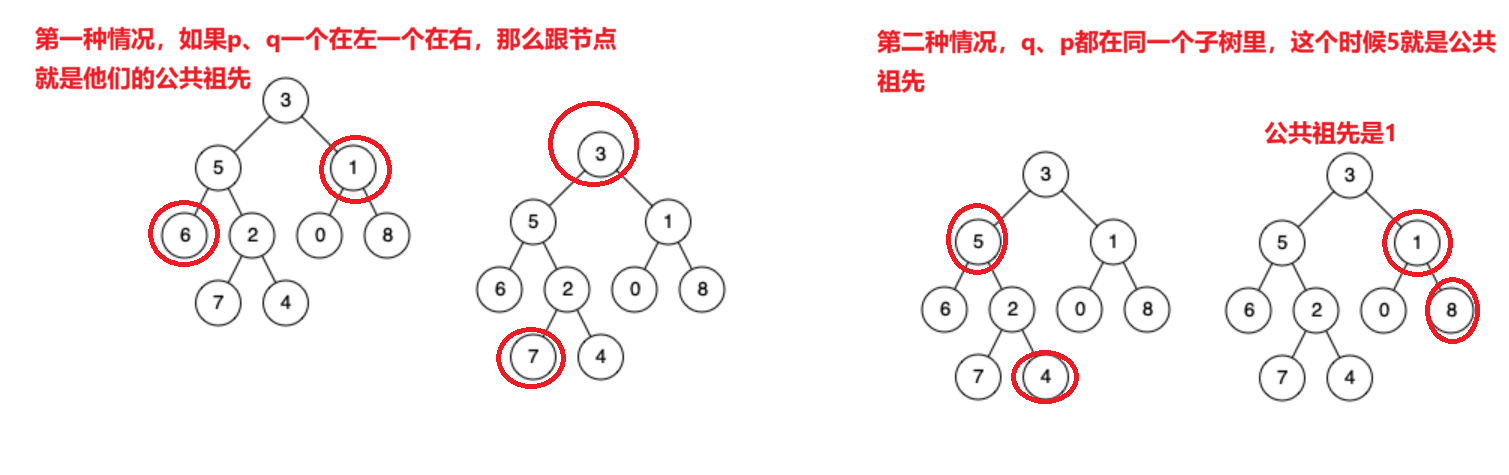
解决思路:
如果是第一种情况,只要判断出p、q其中一个是根节点或者p、q不在同一子树,就可以知道根节点就是公共祖先
如果不是第一种情况,就说明p、q存在于同一个子树,就要递归到其左树去寻找p、q的位置,左树没找到,就递归到右树去找到p、q的位置,在判断是什么情况。
代码如下:
class Solution {
public:
bool Find(TreeNode* root, TreeNode* f)
{
if (root == NULL)
return false;
// f和root不是相同节点,就递归到左子树去找,左子树找不到就递归到右树找
return root == f || Find(root->left, f) || Find(root->right, f);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
// 如果穿了个空树进来,就不用判断了
if (root == NULL)
return NULL;
// 只要p、q有一个是root,其公共祖先就是root了
if (q == root || p == root)
return root;
// 定义四个变量来表示p、q的位置
bool pInLeft, pInRight, qInLeft, qInRight;
pInLeft = Find(root->left, p); // 去左子树找p
pInRight = !pInLeft; // 左子树没找到就在右子树
qInLeft = Find(root->left, q); //去左子树找q
qInRight = !qInLeft;
// 如果一个在左子树,一个在右子树,公共祖先就是root
if ((pInLeft && qInRight) || (pInRight && qInLeft))
return root;
// 如果都在左子树,就要递归到左子树去找
if (pInLeft && qInLeft)
return lowestCommonAncestor(root->left, p, q);
// 如果都在右子树,就要递归到右子树去找
if (pInRight && qInRight)
return lowestCommonAncestor(root->right, p, q);
return NULL;
}
};
5.二叉搜索树和双向链表
二叉搜索树和双向链表

分析:
将二叉搜索树转换为双向链表其实就是修改树节点的left和right指针按照中序遍历指向对应的节点。
这里我们让left指针指向上一个节点,right指向下一个节点

但是这里有个问题,当我们通过中序遍历递归到一个节点的时候,这个节点的right指针是无法指向下一个节点的,因为拿不到另外一层递归深度的节点。因此这里采用双指针来解决这个问题
如下图所示:

注意:在传双指针到函数进行调用的时候,prev要注意得传址或者传引用调用。cur不需要传引用和传址,函数内部不对cur进行赋值操作,不需要改变cur本身,要改变的是cur内部的指针
代码如下:
struct TreeNode
{
int val;
struct TreeNode* left;
struct TreeNode* right;
TreeNode(int x)
:val(x)
,left(NULL)
,right(NULL)
{}
};
class Solution {
public:
// 这里TreeNode*&的引用一定要加,不然就用二级指针。这样才是传址调用
void ConvertList(TreeNode* cur, TreeNode*& prev)
{
if (cur == nullptr)
return;
// 中序遍历
ConvertList(cur->left, prev);
// 这里才是对当前根节点进行处理的地方,在这里连接上一个节点和下一个节点
cur->left = prev; // cur的left指针指向上一个节点
// 只要prev不为空的情况下,就可以让其right指针指向下一个节点
if (prev)
prev->right = cur;
//这里对prev进行赋值,一定要注意是传值还是传址,传值调用会导致上一层的prev无法改变
prev = cur; // 迭代
ConvertList(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
// 空树,无法转换
if (pRootOfTree == nullptr)
return nullptr;
// 双指针解决节点连接问题
TreeNode* prev = nullptr;
TreeNode* cur = pRootOfTree;
ConvertList(cur, prev);
// 此时的双向链表就已经连接完了。
// 此时的树结构被破坏了,但是依旧可以根据left指针或者right指针来找
//一直找上一个节点,来找到第一个节点,或者一直找下一个节点,找到尾节点
TreeNode* head = pRootOfTree;
// 这里不用考虑head是否为nullptr,而导致解引用空指针崩溃
// 因为pRootOfTree走到这里不可能是nullptr
while (head->left != nullptr)
{
head = head->left;
}
return head;
}
};
6.从前序与中序遍历序列构造二叉树
从前序与中序遍历序列构造二叉树
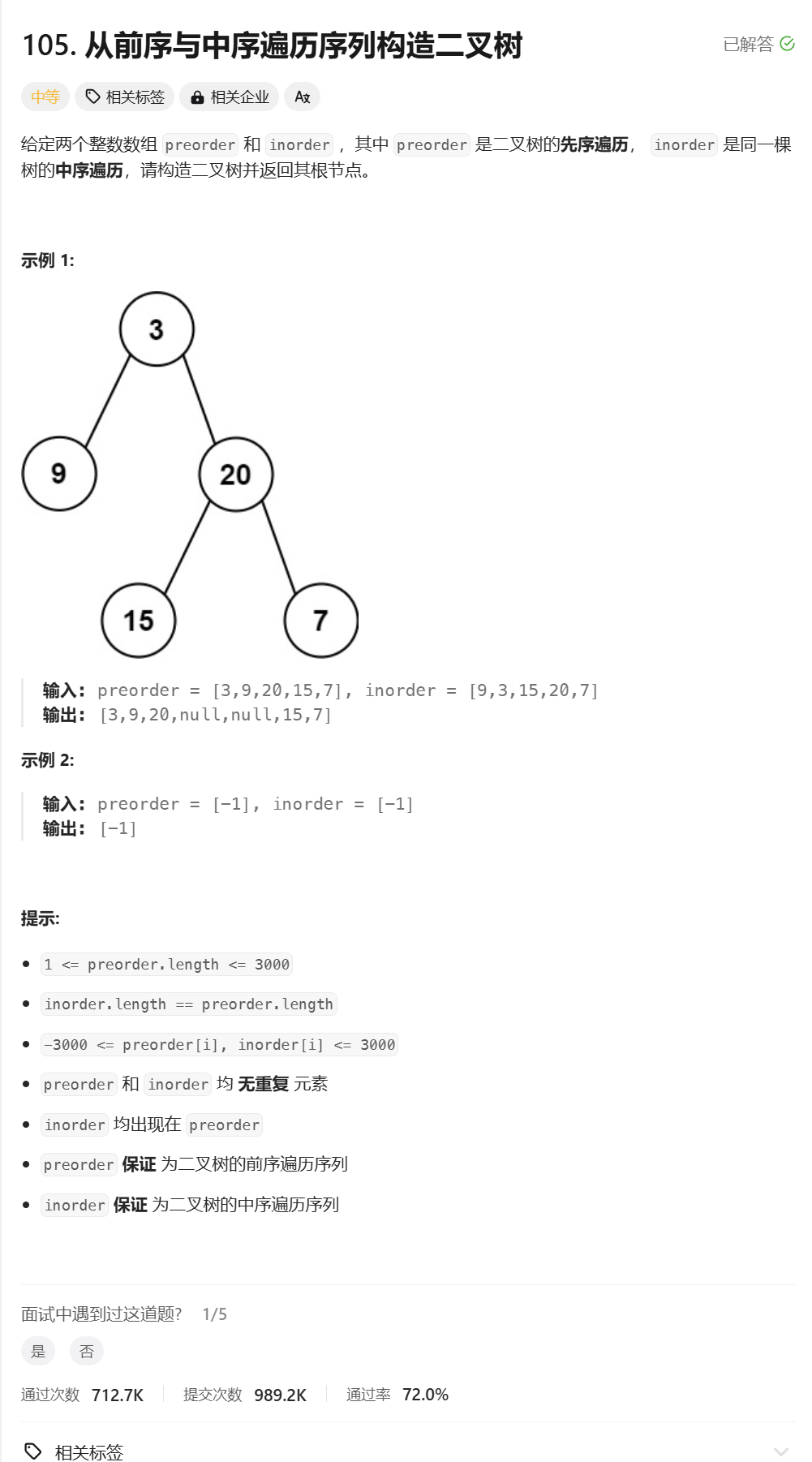
思路分析:

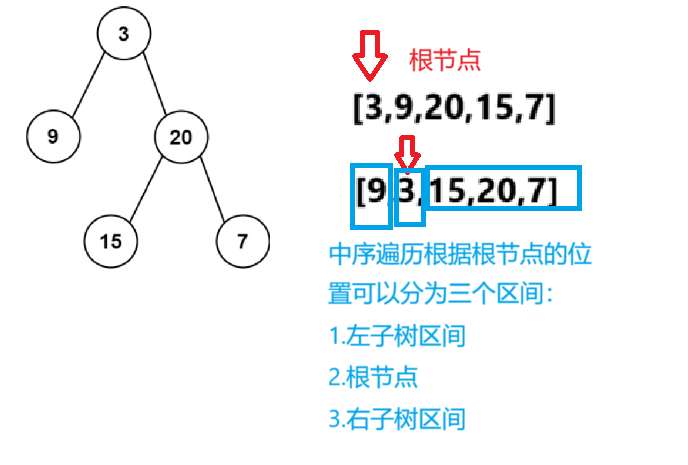
代码实现如下:
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
class Solution {
public:
TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend)
{
// 先构建一个根节点
TreeNode* root = new TreeNode(preorder[prei]);
// 找到中序遍历中根节点的位置
int rooti = inbegin;
while (rooti <= inend)
{
if (inorder[rooti] == preorder[prei])
break;
else
++rooti;
}
// 此时找到了中序遍历的根节点,这个时候可以将中序遍历化为3个区间
// 左子树区间, 根节点,右子树区间
// [inbegin, rooti-1] rooti [rooti+1, inend]
//这个时候还要判断左区间和右区间是否存在,才能去进行递归构建
if (inbegin <= rooti - 1)
root->left = _buildTree(preorder, inorder, ++prei, inbegin, rooti - 1);
else
root->left = nullptr; // 左子树不存在了,连接空
// 构建完左子树之后,才构建右子树,同样的也要判断,是否存在右子树区间
if (rooti + 1 <= inend)
root->right = _buildTree(preorder, inorder, ++prei, rooti + 1, inend);
else
root->right = nullptr;
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
// 如果是空的就不用构建了
if (inorder.empty() || preorder.empty())
return nullptr;
//确定根节点的下标和中序遍历的范围
int prei = 0;// 这个是前序遍历的下标,prei指向的是待构建的节点
int inbegin = 0;
int inend = inorder.size() - 1;
TreeNode* ret = _buildTree(preorder, inorder, prei, inbegin, inend);
return ret;
}
};
注意:
这道题的本质还是通过preorder中的前序遍历来构建二叉树,但是我们并不知道prei所指向的节点到底是左子树的节点还是右子树的节点。因此我们通过中序遍历来划分区间,从而来确定prei所指向的节点是左子树的还是右子树的节点。
7.从中序和后序遍历序列来构造二叉树
从中序与后序遍历序列构造二叉树
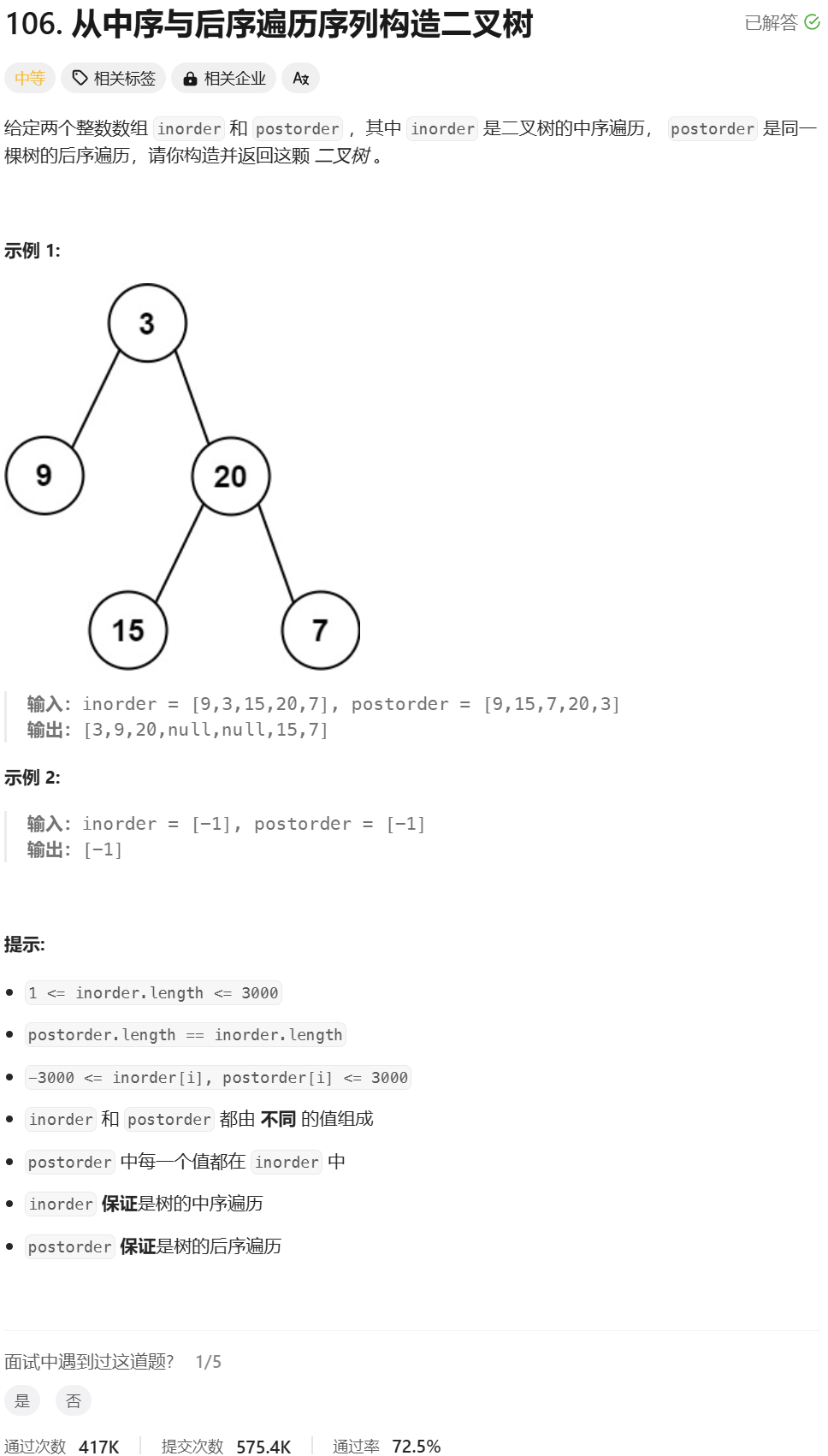
分析:
这个和第六题是非常像的,不一样的是,这里通过后序遍历来确定根节点的位置。中序排序的作用还是划分左子树和右子树的区间,这样才能确定根据后序遍历序列的节点左子树的节点还是右子树的节点、
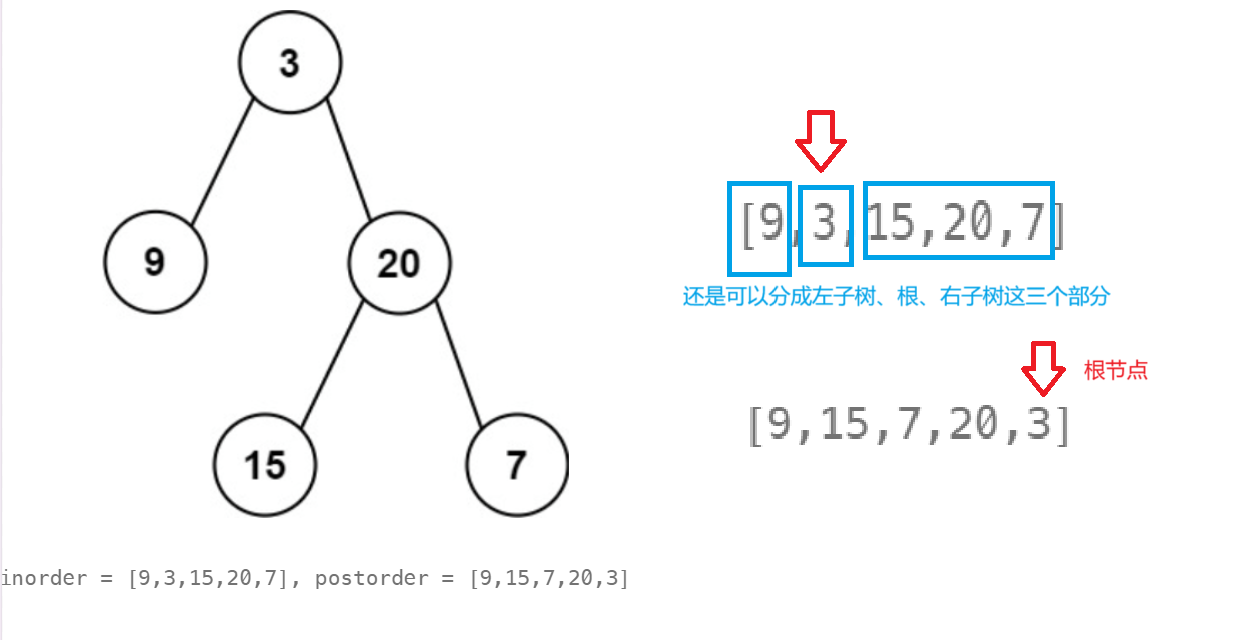
当构建完3这个根节点之后,构建20这个根节点,递归进去。
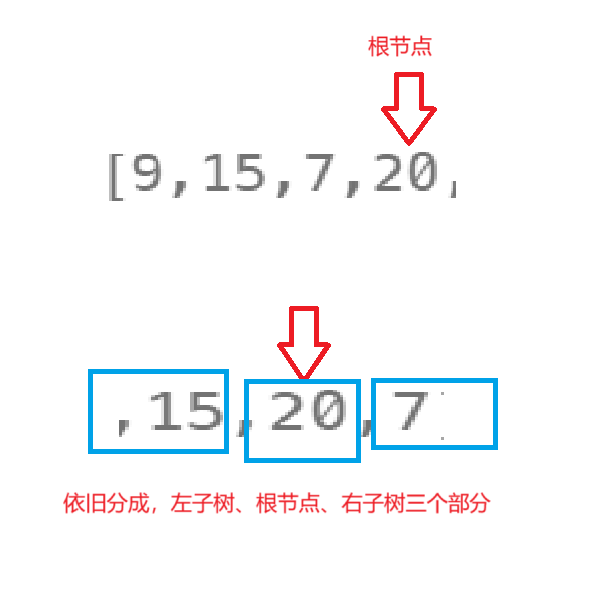
依次类推,最终构建出右子树,在构建左子树
要想彻底理解过程,可以画出每个节点被创建出来后是如何连接到一起的。
代码如下:
class Solution {
public:
TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posi, int inbegin, int inend)
{
TreeNode* root = new TreeNode(postorder[posi]);
//在中序遍历序列中找到根节点
int rooti = inbegin;
while(rooti <= inend)
{
if(inorder[rooti] == postorder[posi])
break;
else
++rooti;
}
// 找到了根节点就要划分区域————左子树、根、右子树
// [inbegin, rooti - 1] rooti [rooti + 1, inend]
if(rooti+1 <= inend)
root->right = _buildTree(inorder, postorder, --posi, rooti+1, inend);
else
root->right = nullptr;
// 先构建完右子树后,再来构建左子树
if(inbegin <= rooti-1)
root->left = _buildTree(inorder, postorder, --posi, inbegin, rooti-1);
else
root->left = nullptr;
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
{
// 如果是空的就不用构建了
if(inorder.empty() || postorder.empty())
return nullptr;
int posi = postorder.size() - 1;
int inbegin = 0;
int inend = inorder.size() - 1;
TreeNode* ret = _buildTree(inorder, postorder, posi, inbegin, inend);
return ret;
}
};
要注意:
无论是第六题还是本题,prei和posi的形参都必须加上引用或者是指针,不然的话,递归深了,对其进行++,上一层递归深度的函数的posi是不会变化的。
8.二叉树的前序遍历,非递归迭代实现
二叉树的前序遍历
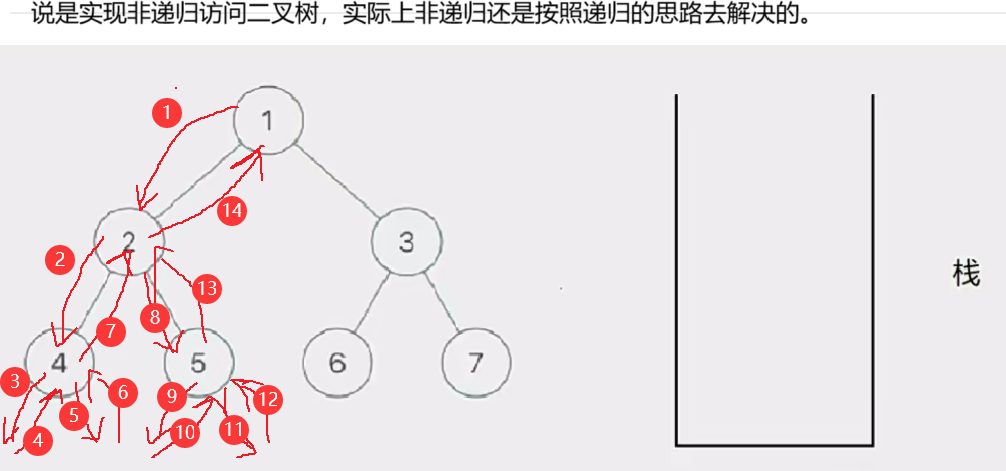
在递归实现前序遍历二叉树的时候,我们发现访问的节点可以分为两类:
- 左路节点
- 左路节点的右子树
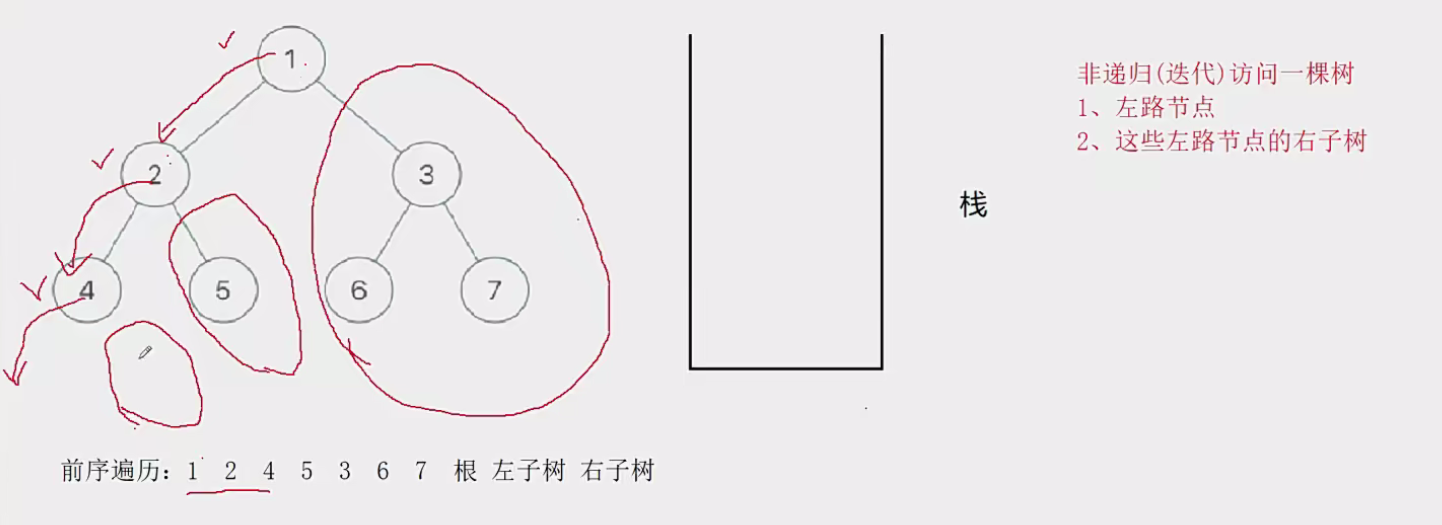
因此我们只需要将整颗树分成左路节点和左路节点的右子树来访问就行了
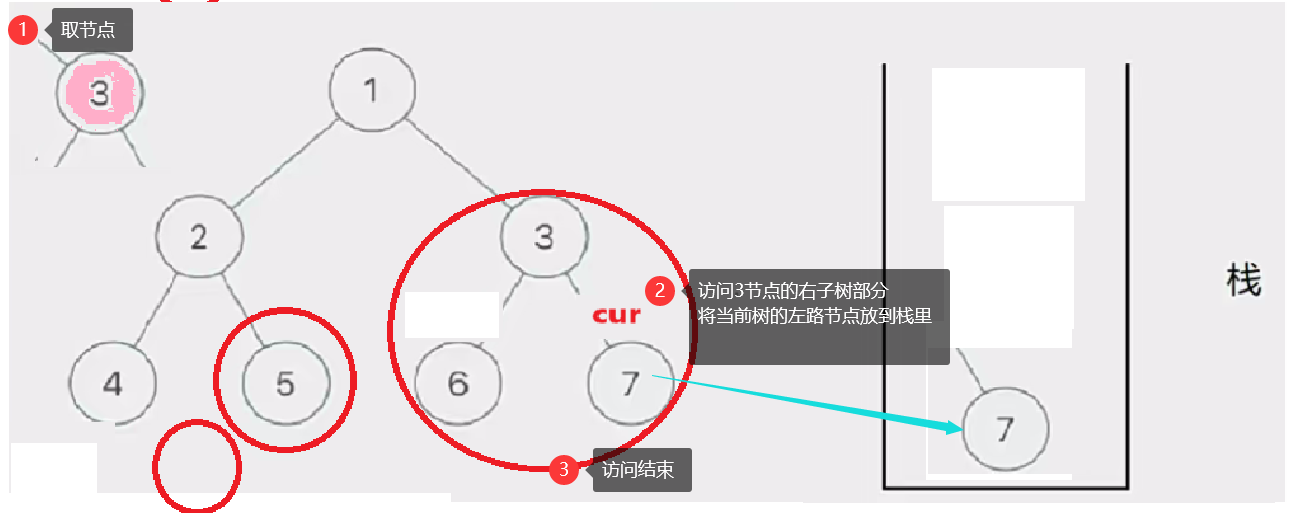
那如何访问左路节点呢——我们需要借助一个栈
将所有左路节点放到一个栈里
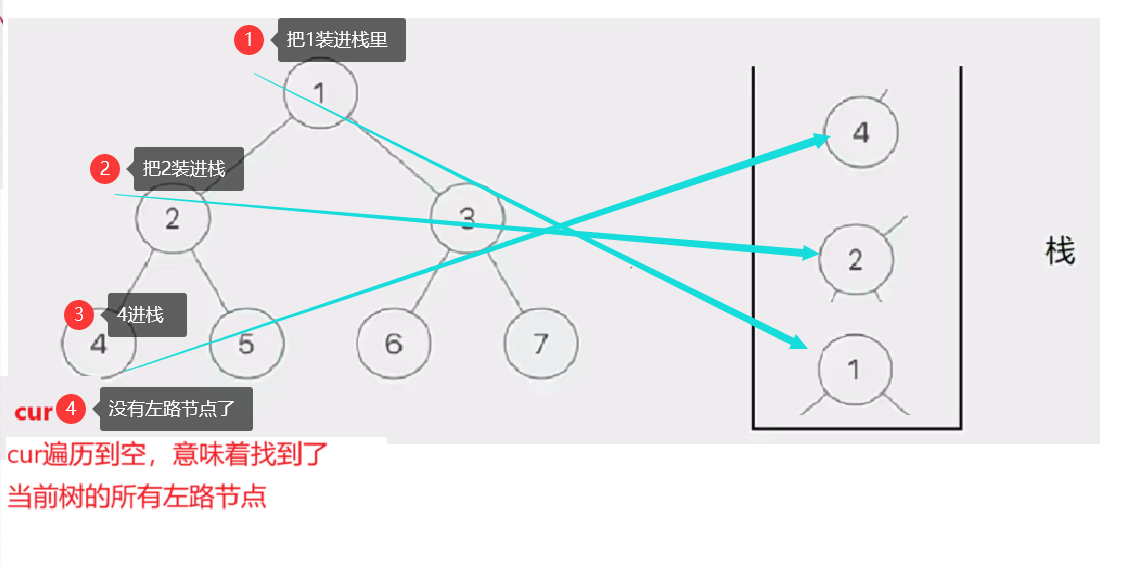
此时有三个圈,代表当前树的三个左路节点的右子树部分
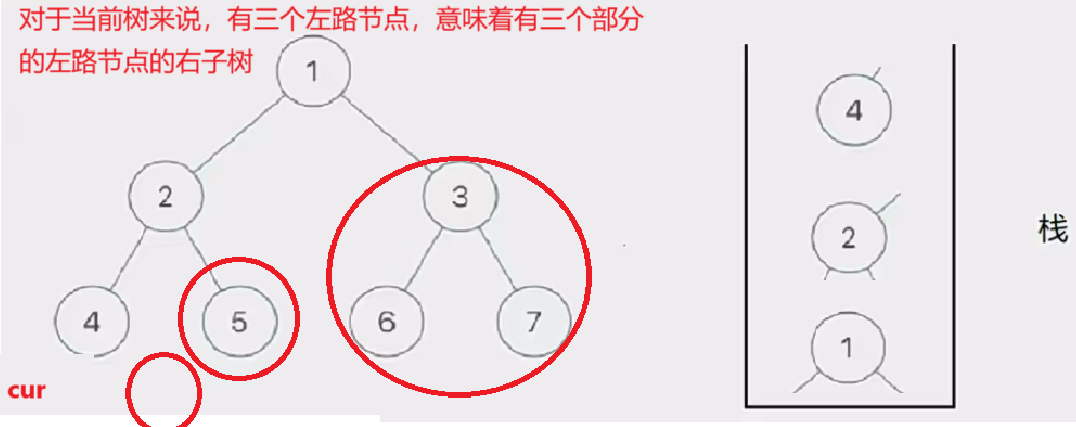
然后我们取栈里的左路节点出来,依次访问他们的右子树部分。
要注意这个访问右子树的过程是将右子树也看成一棵树来看待的,也就是说将这个右子树分成左路节点和左路节点的右子树两个部分查看。这个思路就是模仿递归的思路。只是我们通过迭代来实现这个过程
这个去栈的左路节点访问右子树部分的过程如下图所示:
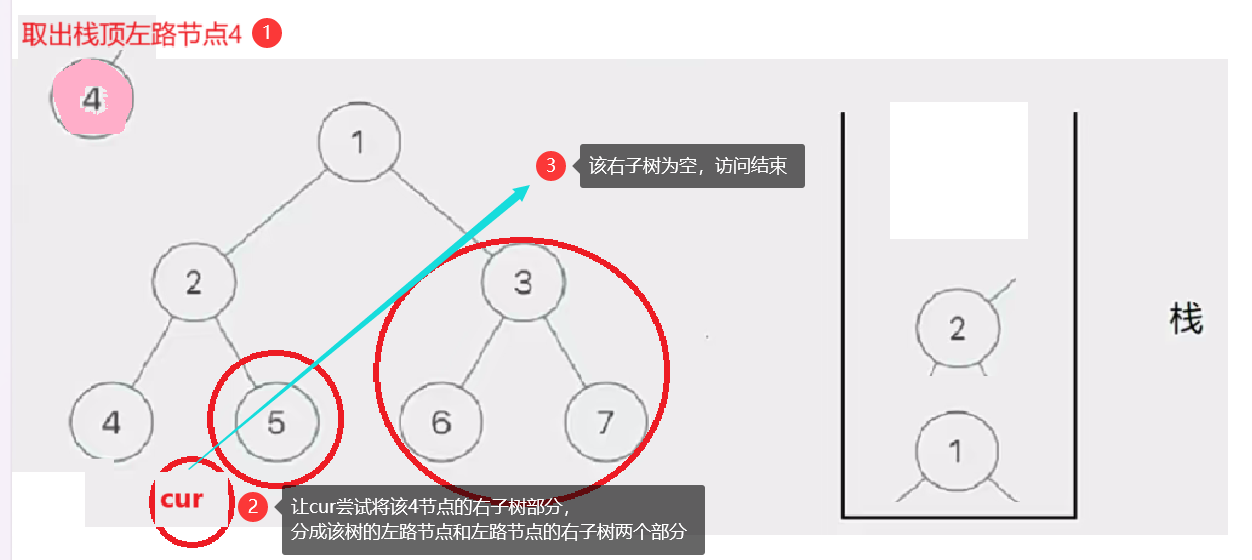
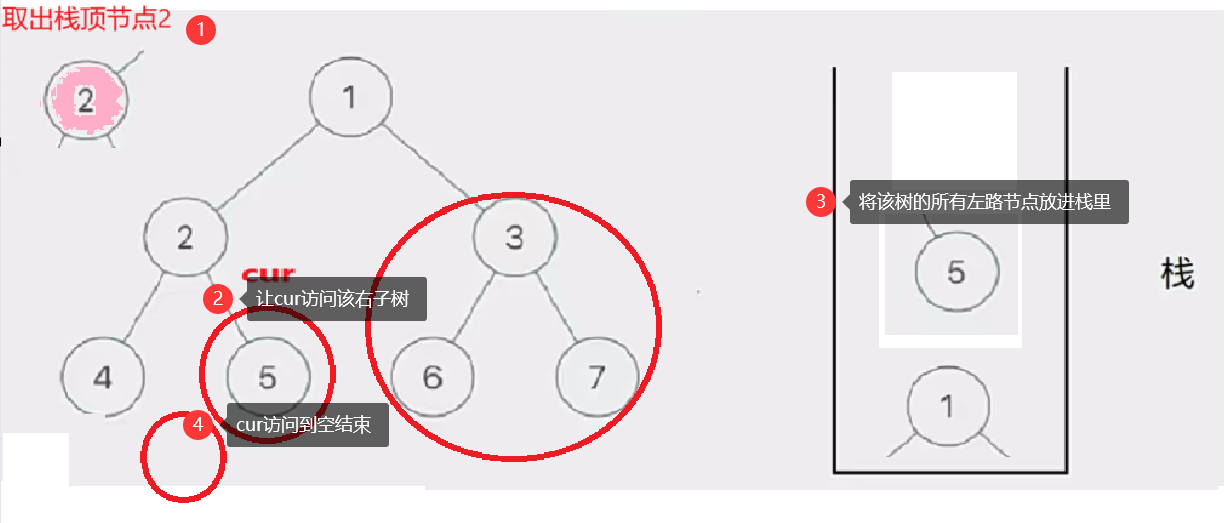
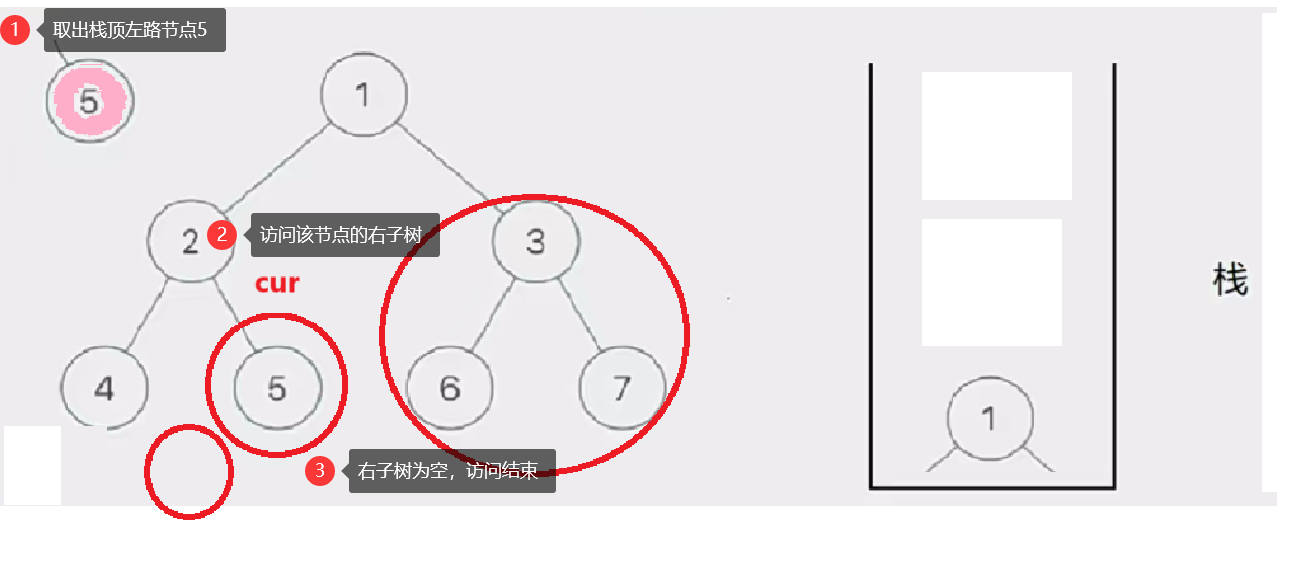
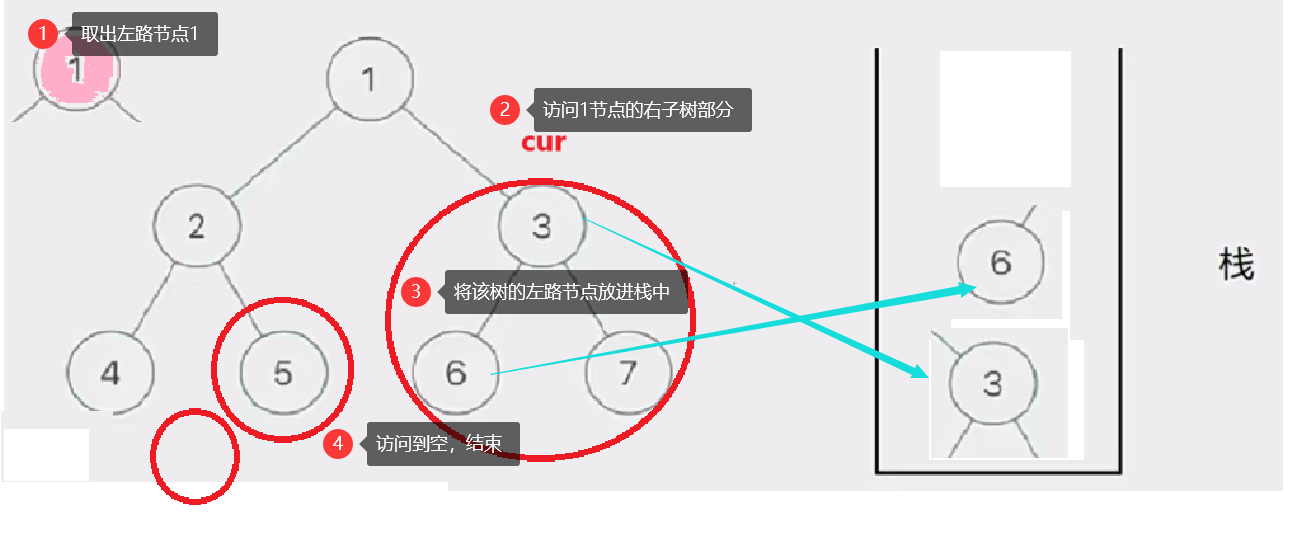
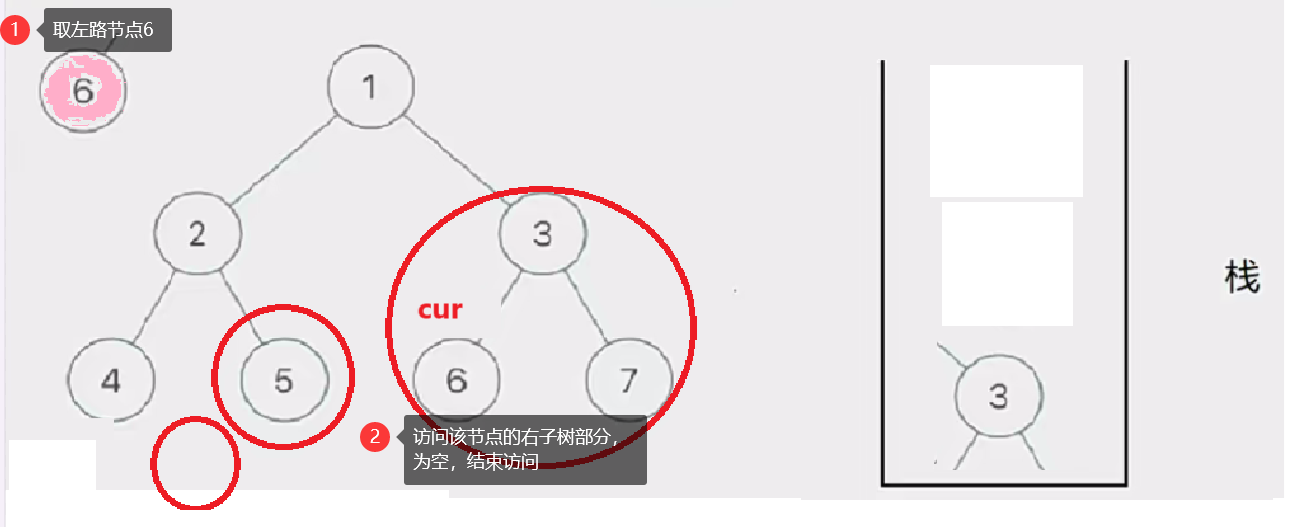
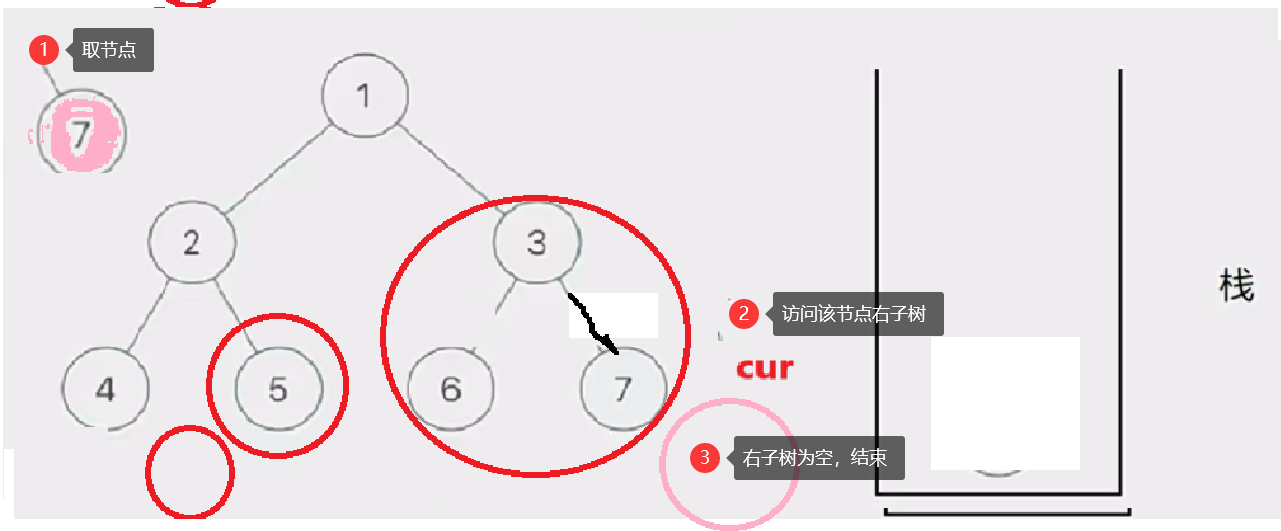
此时cur为空,栈也为空,意味访问结束,树已前序遍历完成
代码如下:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root)
{
vector<int> ret;
// 借助栈实现非递归的前序遍历二叉树
stack<TreeNode*> st;
TreeNode* cur = root;
// 当cur和栈都为空的时候意味着遍历完成
while(cur || !st.empty())
{
// 访问当前cur这棵树的所有左路节点并放到栈中
while(cur)
{
ret.push_back(cur->val);
st.push(cur);
cur = cur->left;
}
// 取栈内的左路节点,并访问其右子树
TreeNode* top = st.top();
st.pop();
cur = top->right;
}
// 此时ret中存放着前序遍历的数字
return ret;
}
};
9.二叉树中序遍历 ,非递归迭代实现
二叉树的中序遍历
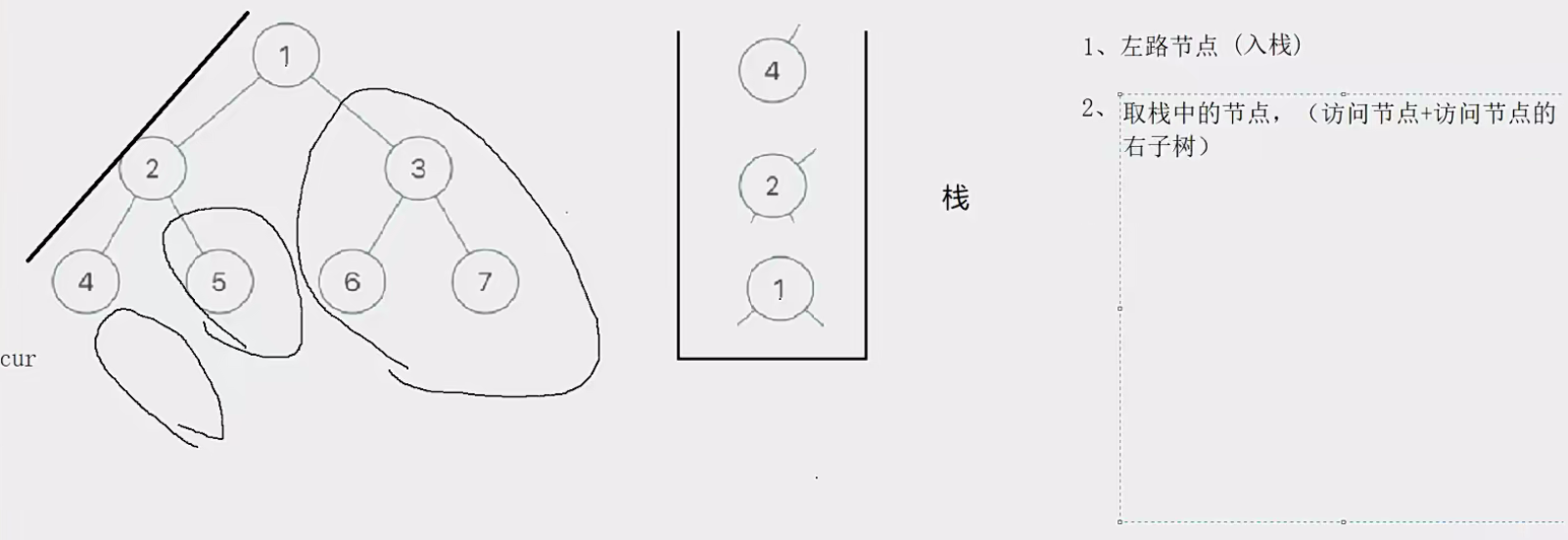
这个题和前序遍历的思路是一样的,唯一的区别就是让左路节点入栈的时候,不能访问,取左路节点的时候,才访问该节点,并访问该节点的右子树。
代码如下:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root)
{
vector<int> ret;
stack<TreeNode*> st; // 借助栈实现非递归中序遍历
TreeNode* cur = root;
// 当cur和栈同时为空,才意味着遍历完成
while(cur || !st.empty())
{
// 将当前cur这棵树的所有左路节点放到栈中
while(cur)
{
// 中序遍历,这里只入栈,不访问节点
st.push(cur);
cur = cur->left;
}
// 取左路节点出来,访问该左路节点
//并且访问该左路节点的右子树
TreeNode* top = st.top();
st.pop();
ret.push_back(top->val); // 放问该左路节点
cur = top->right; // 指向该左路节点右子树,下一循环访问该树
}
// 返回ret,中序遍历的结果
return ret;
}
};
10.二叉树的后序遍历 ,非递归迭代实现
二叉树的后序遍历
这里的后序遍历,需要在前两题的思路上变动一下。
大致思路不变,还是将整颗树分成左路节点和左路节点的右子树两个部分。将当前树的左路节点放到栈里,然后从栈中取左路节点出来,由于是后序,不访问左路节点,也不能将其从栈内弹出,要先访问其右子树。
这里访问右子树有两种情况:
-
如果右子树是空,那么就访问这个左路节点,并弹出
-
如果右子树不为空,那么就访问右子树,并不弹出该左路节点【仍然将这个右子树分两个部分处理】
但是有一个难点就在这里,如果右子树不为空,由于上一个左路节点未弹出,如下图的2节点,就会访问两次,这个时候如何区分5这个右子树是否被访问过了?
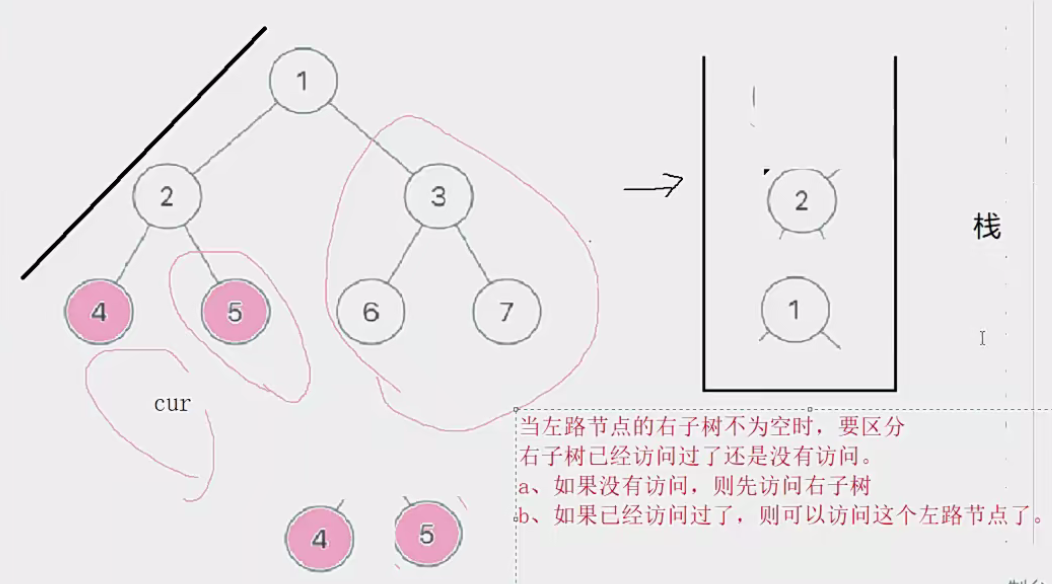
如果区分不出来那么程序就会陷入死循环。
解决思路:
- 弄一个储存标志位的栈,只要遇到右子树不是空,就给该右子树弄一个标志位,并存到栈中,等到第二次访问该节点的时候,通过取出这个标志位,判断该节点是否被访问过。
- 双指针,一个指针指向当前访问节点,一个指针指向上一个节点,因为后序遍历顺序是左子树、根、右子树、**因此当我想访问一个左路节点的时候,其双指针一定待在该左路节点的右孩子当中。比如访问2,双指针的另一个指针就在5。**但是我第一次取到2,不能访问2,要判断其2的右子树是否被访问过,只要双指针不在其右子树,就说明没有被访问过。
代码如下:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root)
{
vector<int> ret;
stack<TreeNode*> st; // 用栈辅助实现非递归后序遍历二叉树
// 用双指针解决——如何判断左路节点的右子树是否被访问过的问题
TreeNode* cur = root;
TreeNode* lastNode = nullptr; // lastNode由于记载栈顶的左路节点的右子树是否被访问过
// 当cur和栈都为空,才是遍历完二叉树
while(cur || !st.empty())
{
// 先把当前树的所有左路节点放到栈里
while(cur)
{
st.push(cur);
cur = cur->left;
}
// 拿到栈顶的左路节点
TreeNode* top = st.top();
// 由于是后序,先判断栈顶元素的右子树是否被访问过.
if(top->right == nullptr || lastNode == top->right)
{
// 只要右子树为空,或者是右子树被访问过,那么就不需要在访问当前左路节点的右子树。
ret.push_back(top->val); // 访问当前左路节点
st.pop(); // 可以弹出该左路节点
lastNode = top; // 更新lastNode的位置,保持其一直位于top的上一个访问节点
}
else
{
// 访问当前左路节点的右子树
cur = top->right;
}
}
// 返回后序遍历
return ret;
}
};