文章目录

前言
题单
- hdu2044 一只小蜜蜂...
- hdu2045 不容易系列之(3)—— LELE的RPG难题
- hdu2046 骨牌铺方格
- hdu2047 阿牛的EOF牛肉串
- hdu2048 神、上帝以及老天爷
- hdu2049 不容易系列之(4)——考新郎
- hdu2050 折线分割平面
END

前言

题单：递推求解专题练习（For Beginner）

这是(hdu.edu.cn) 一份非常经典的dp递推求解的题单

起始本质是一堆线性dp

虽说是For Beginner，但博主做的时候还是吃了很多憋的

可能博主还处于beginner的阶段吧

下文中题意直接略

题单

hdu2044 一只小蜜蜂…

观察到每个点只有由左侧相邻的两个点转换而来

这两个点分别为x-1和x-2

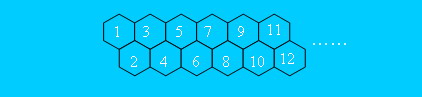
C40-1001-1.jpg (422×97) (hdu.edu.cn)

从起点到终点

/**
 * https://acm.hdu.edu.cn/showproblem.php?pid=2044
 * 一只小蜜蜂...
 * 斐波那契数列变体
 */
#include <bits/stdc++.h>
using namespace std;

void solve() {
    int x, y;
    cin >> x >> y;

    vector<long long> dp(y + 1);
    dp[x] = 1;
    dp[x + 1] = 1;
    for (int i = x + 2; i <= y; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    cout << dp[y] << endl;
}

int main() {
    int x = 1;
    cin >> x;

    while (x--) {
        solve();
    }

    return 0;
}

打表+偏移量

/**
 * https://acm.hdu.edu.cn/showproblem.php?pid=2044
 * 一只小蜜蜂...
 * 斐波那契数列变体
 */
#include <bits/stdc++.h>
using namespace std;

int main() {
    vector<long long> dp(50 + 1);
    dp[1] = 1;
    dp[2] = 1;
    for (int i = 3; i < dp.size(); i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    int T = 1;
    cin >> T;

    while (T--) {
        int x, y;
        cin >> x >> y;
        cout << dp[y - x + 1] << endl;
    }

    return 0;
}

hdu2045 不容易系列之(3)—— LELE的RPG难题

类似的思考方式的题

专题：(经典dp) I型 L型铺盖2*n_天赐细莲的博客-CSDN博客

一道很不错的线性dp推到题

限制了两个条件

相邻状态不能相同
不能和首位置相同

线性dp

从尾位置开始往前推导

/**
 * https://acm.hdu.edu.cn/showproblem.php?pid=2045
 * 不容易系列之(3)—— LELE的RPG难题
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long

const int M = 10 + 50;
// 定义第i位的可能情况
int dp[M];

int __init__ = []() {
    // 根据下面的推到，要求dp[i-2]
    // 因此手动推到出前三项
    dp[1] = 3;
    dp[2] = 6;
    dp[3] = 6;

    // 考虑第i个位置
    // 1. 若i-1与1不同 则i确定 dp[i-1]
    // 2. 若i-1与1相同 则i与i-1不同的两种 理想状态是 2*dp[i-1]
    // 但这个dp[i-1]的i-1位是记录与1不同的
    // 因此直接考虑，i-1位和1相同的情况
    // 显然确定了一个颜色后，前面只能放另外2种 => dp[i-2]*2
    // 综上：dp[i] = dp[i-1] + 2 * dp[i-2]
    for (int i = 4; i < M; i += 1) {
        dp[i] = dp[i - 1] + 2 * dp[i - 2];
    }
    return 0;
}();

signed main() {
    int n;
    while (cin >> n) {
        cout << dp[n] << endl;
    }
    return 0;
}

状态机dp

全网大都是线性dp的思路，但这个也是典型的状态机dp的题

我一开始定义的状态机为dp[i][j] 直接考虑到第i个位置，填颜色j的种类总数

但是这么定义死活不能ac，因为相邻是好推导的，难点在于如何考虑首尾不同这个限制

本来想再加一个维度表示相同和不同，但是还是没写出来

最后再搜了大量博客后终于找到了一篇，定义的含义为**针对起始的一种颜色**，末尾放三种的可能性

最后只要*3即可，豁然开朗

/**
 * https://acm.hdu.edu.cn/showproblem.php?pid=2045
 * 不容易系列之(3)—— LELE的RPG难题
 * ==============================================
 * 状态机dp
 * 增加一个维度表示末尾放到是什么颜色
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long

const int M = 10 + 50;
// 定义dp[i][3]
// **针对起始的一种颜色**，末尾放三种的可能性
int dp[M][3];

int __init__ = []() {
    // 假设考虑的颜色为0号
    dp[1][0] = 1;
    dp[1][1] = 0;
    dp[1][2] = 0;
    for (int i = 2; i < M; i += 1) {
        // 相邻的颜色不同
        dp[i][0] = dp[i - 1][1] + dp[i - 1][2];
        dp[i][1] = dp[i - 1][0] + dp[i - 1][2];
        dp[i][2] = dp[i - 1][0] + dp[i - 1][1];
    }
    return 0;
}();

signed main() {
    int n;
    while (cin >> n) {
        if (n == 1) {
            // n=1特判
            // 因为n为1时，首位和末尾是相同的
            cout << 3 << endl;
        } else {
            // 三种颜色 *3
            // 计算时，假设的起始颜色为0，则末尾不算0的情况
            cout << (dp[n][1] + dp[n][2]) * 3 << endl;
        }
    }

    return 0;
}

hdu2046 骨牌铺方格

专题：(经典dp) 骨牌问题 2n 3n n*m_天赐细莲的博客-CSDN博客

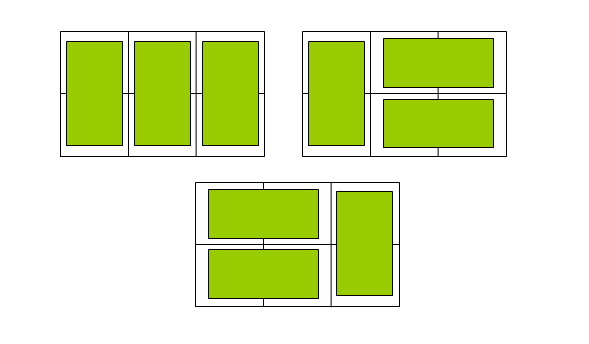
C40-1003-1.jpg (589×344) (hdu.edu.cn)

太经典了，这个问题

假设最后一个块竖着放，则由dp[i-1]推导来
假设最后一个块横着放，则必须两个块一起横着放，由dp[i-2]推导来

/**
 * 专题博客：https://blog.csdn.net/CUBE_lotus/article/details/127895641
 * https://acm.hdu.edu.cn/showproblem.php?pid=2046
 * 骨牌铺方格
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long

const int M = 10 + 50;

int dp[M];

int __init__ = []() {
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i < M; i += 1) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return 0;
}();

signed main() {
    int n;
    while (cin >> n) {
        cout << dp[n] << endl;
    }
    return 0;
}

hdu2047 阿牛的EOF牛肉串

也是一道经典的状态机dp，难度限制只有相邻的状态

把状态值定义在第一维的一个好处

可以便捷初始化这个状态的所有值 memset(dp[state], 0, sizeof(dp[state]))

/**
 * https://acm.hdu.edu.cn/showproblem.php?pid=2047
 * 阿牛的EOF牛肉串
 * 以后缀分析问题
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long
// 长度40了，记得开long long
int dp[3][40 + 1];
signed main() {
    dp[0][1] = 1;
    dp[1][1] = 1;
    dp[2][1] = 1;

    for (int i = 2; i <= 40; i++) {
        dp[0][i] = dp[0][i - 1] + dp[1][i - 1] + dp[2][i - 1];
        dp[1][i] = dp[0][i - 1] + dp[1][i - 1] + dp[2][i - 1];
        dp[2][i] = dp[0][i - 1] + dp[1][i - 1];
    }

    int n;
    while (cin >> n) {
        cout << dp[0][n] + dp[1][n] + dp[2][n] << endl;
    }

    return 0;
}

hdu2048 神、上帝以及老天爷

概率相关的题我直接跪

参考博客：[航电ACM hdu-2048] 神、上帝以及老天爷_Litmmp的博客-CSDN博客

了解到了这个错排公式

错排公式_百度百科

/**
 * https://acm.hdu.edu.cn/showproblem.php?pid=2048
 * 神、上帝以及老天爷
 * ==============================================
 * 求没人中将的百分比
 * ==============================================
 * 参考博客：
 * https://blog.csdn.net/u011506951/article/details/25157161
 */
#include <bits/stdc++.h>
using namespace std;

const int M = 10 + 20;
double dp[M];

int __init__ = []() {
    // 求分母，即 n!
    double denominator[M];
    denominator[1] = 1.0;
    for (int i = 2; i < M; i += 1) {
        denominator[i] = denominator[i - 1] * i;
    }

    // 分子
    /*
    dp[] 表示考虑到i个人都是错态的种类
    若i拿了自己的票，则与i-1人交换即可
    (i-1)*dp[i-1]

    若i-1人中有人拿了自己的票，则无论i拿的是不是，只要和那个拿了自己票的交换即可
    i-1中除去拿自己票的有i-2人
    (i-1)*dp[i-2]
    */
    double molecule[M];
    molecule[1] = 0;
    molecule[2] = 1;
    for (int i = 3; i < M; i += 1) {
        molecule[i] = (i - 1) * (molecule[i - 1] + molecule[i - 2]);
    }

    for (int i = 1; i < M; i += 1) {
        dp[i] = molecule[i] / denominator[i];
    }
    return 0;
}();

signed main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        printf("%.2lf%%\n", dp[n] * 100);
    }
    return 0;
}

hdu2049 不容易系列之(4)——考新郎

错排公式_百度百科

组合数_百度百科

错排公式+组合数

/**
 * https://acm.hdu.edu.cn/showproblem.php?pid=2049
 * 不容易系列之(4)——考新郎
 * ===============================================
 * N对新婚夫妇,其中有M个新郎找错了新娘
 * 求发生这种情况一共有多少种可能
 * 错态 * 组合
 */
#include <bits/stdc++.h>
using namespace std;
#define int long long

const int M = 10 + 20;
// 表示前i个数的错态种类(位置全不对)
int dp[M];

int __init__ = []() {
    dp[1] = 0;
    dp[2] = 1;
    for (int i = 3; i < M; i++) {
        dp[i] = (i - 1) * (dp[i - 1] + dp[i - 2]);
    }

    return true;
}();

// 组合数公式
// n个数中取m个求组合数
inline int Combination(int m, int n) {
    int ans = (m <= n);
    m = min(m, n - m);
    for (int i = 0; i < m; i++) {
        ans *= n - i;
    }
    for (int i = 1; i <= m; i++) {
        ans /= i;
    }
    return ans;
}

signed main() {
    int T, n, m;
    cin >> T;
    while (T--) {
        cin >> n >> m;
        // 错态*组合
        cout << dp[m] * Combination(m, n) << endl;
    }

    return 0;
}

排列组合公式

排列组合百度百科

排列

$A^{m}_{n} = n(n-1)(n-2)···(n-m+1) = {n!\over(n-m)!} \\[2ex] 共m个因子累乘\quad n >= m$

组合
$C^{m}_{n} = {A^{m}_{n}\over {m!}} = {n!\over {m!(n-m)!}} \\[2ex] C^{m}_{n} = C^{n-m}_{n} \qquad n >= m$

计算举例：

$\qquad \qquad C^{3}_{5} = C^{2}_{5} \\[2ex] 计算 \qquad \qquad {5*4*3 \over 3*2*1} = {5*4 \over 2*1} \qquad 分子分母各m个数累乘 \\[2ex] C^{3}_{5} = {5*(5-1)*(5-2) \over 1*2*3}$

问题举例：

有1个A,2个B,3个C 共有多少种排列
${6!\over 1! * 2! * 3!}$

// n个中选m个
inline int Combination(int m, int n) {
    int ans = (m <= n);
    m = min(m, n - m);
    for (int i = 0; i < m; i++) {
        ans *= n - i;
    }
    for (int i = 1; i <= m; i++) {
        ans /= i;
    }
    return ans;
}

hdu2050 折线分割平面

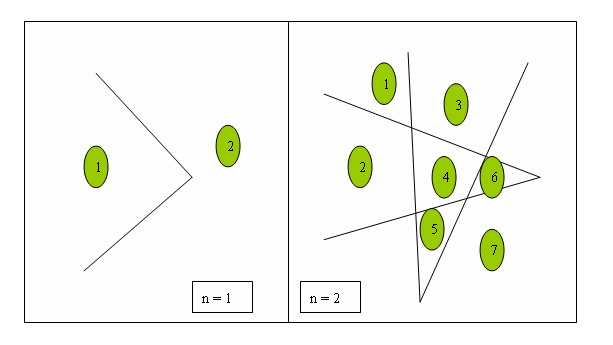
C40-1008-1.jpg (613×345) (hdu.edu.cn)

画图分析，有多少个折线的焦点

/**
 * https://acm.hdu.edu.cn/showproblem.php?pid=2050
 * 折线分割平面
 */
#include <bits/stdc++.h>
using namespace std;

int main() {
    vector<long long> dp(10000 + 10);
    dp[1] = 2;
    for (int i = 2; i < dp.size(); i++) {
        // 首先获取上一轮的值
        // 再计算，与之前的每一条线都有4个焦点，每个焦点贡献出一块区域
        // 最后自己的小尖角
        dp[i] = dp[i - 1] + 4 * (i - 1) + 1;
    }

    int T = 1;
    cin >> T;

    while (T--) {
        int x;
        cin >> x;
        cout << dp[x] << endl;
    }

    return 0;
}