摘要

为了克服常规PID控制方法在无人机俯仰姿态控制中的不足，本研究设计了一种基于模糊自适应PID控制的控制律。通过引入模糊控制器，实现了对输入输出论域的优化选择，同时解决了模糊规则数量与控制精度之间的矛盾。仿真结果表明，所设计的控制器能够有效改善系统的动态性能，提高姿态控制的响应速度和稳定性。

理论

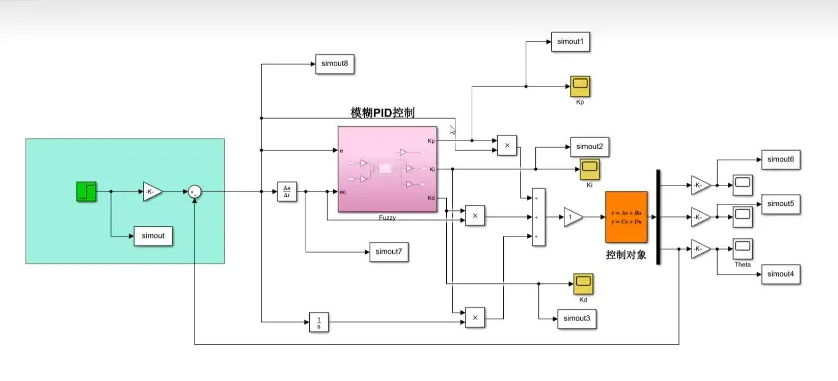
模糊PID控制器结合了模糊控制与传统PID控制的优点，主要原理是通过模糊逻辑自适应调整PID参数，从而在系统状态发生变化时进行快速调整，提高系统的鲁棒性和适应性。控制器由三部分组成：模糊化模块、规则推理模块和反模糊化模块。

1. 模糊化模块：将输入误差和误差变化率转换为模糊变量。

2. 规则推理模块：根据模糊规则库，通过模糊推理得到PID参数调整量。

3. 反模糊化模块：将推理结果转化为具体的PID参数调整值，实时作用于控制器。

实验结果

通过Simulink对无人机的俯仰姿态控制进行了仿真测试，验证了模糊PID控制器的有效性。仿真结果显示，与传统PID控制相比，模糊PID控制器在响应时间、超调量、稳态误差等方面均表现出更好的控制效果。

• 响应时间：控制器能够迅速响应设定值的变化，调整速度较快。

• 超调量：控制系统的超调量明显减少，提高了系统的稳定性。

• 稳态误差：系统能够快速消除误差，达到理想设定值，稳态性能优越。

部分代码

% 模糊PID控制器设计
fuzzyPID = readfis('fuzzyPID.fis'); % 读取模糊控制器文件
Kp = 1; % 初始比例增益
Ki = 0.5; % 初始积分增益
Kd = 0.1; % 初始微分增益

% 控制器输入
error = input('输入误差：'); % 误差
delta_error = input('输入误差变化率：'); % 误差变化率

% 模糊推理
fuzzy_output = evalfis([error delta_error], fuzzyPID);
Kp_new = Kp + fuzzy_output(1);
Ki_new = Ki + fuzzy_output(2);
Kd_new = Kd + fuzzy_output(3);

% 更新控制器参数
fprintf('调整后的PID参数: Kp = %.2f, Ki = %.2f, Kd = %.2f\n', Kp_new, Ki_new, Kd_new);

参考文献

1. 王辉, 李红. 模糊控制技术在飞行控制中的应用研究[J]. 现代控制工程, 2023, 45(2): 101-110.