目录
一、Dijkstra算法
实现方式
1、使用优先队列(最小堆)
2、朴素法(简单数组)
二、经典例题
题目:卡码网 47. 参加科学大会
题目链接
题解:朴素Dijkstra
三、小结
一、Dijkstra算法
刚入门Dijkstra算法,可以看一下这个视频:最短路径查找—Dijkstra算法。
定义
Dijkstra算法是一种用于在带权图中找到从单一源点出发到所有其他顶点的最短路径的贪心算法。
实现方式
Dijkstra算法主要有两种实现方式:使用优先队列(通常是最小堆)和朴素法(使用简单的数组)。
1、使用优先队列(最小堆)
伪代码:
DIJKSTRA(G, s)
dist[s] <- 0
prev[s] <- NULL
for each vertex v in G.V - {s}
dist[v] <- INFINITY
prev[v] <- NULL
Q <- priority queue containing all vertices in G.V with dist as key
while Q is not empty
u <- Q.extractMin()
for each vertex v in G.Adj[u]
if dist[u] + G.w(u, v) < dist[v]
dist[v] <- dist[u] + G.w(u, v)
prev[v] <- u
Q.decreaseKey(v, dist[v])
return dist[], prev[]
2、朴素法(简单数组)
伪代码:
DIJKSTRA(G, s)
dist[s] <- 0
prev[s] <- NULL
for each vertex v in G.V - {s}
dist[v] <- INFINITY
prev[v] <- NULL
while there are unvisited vertices
u <- vertex with min dist[u] among unvisited vertices
mark u as visited
for each vertex v in G.Adj[u]
if dist[u] + G.w(u, v) < dist[v]
dist[v] <- dist[u] + G.w(u, v)
prev[v] <- u
return dist[], prev[]
二、经典例题
题目:卡码网 47. 参加科学大会
题目链接
47. 参加科学大会(第六期模拟笔试) (kamacoder.com)
题目描述
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。
小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。
小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。
输入描述
第一行包含两个正整数,第一个正整数 N 表示一共有 N 个公共汽车站,第二个正整数 M 表示有 M 条公路。
接下来为 M 行,每行包括三个整数,S、E 和 V,代表了从 S 车站可以单向直达 E 车站,并且需要花费 V 单位的时间。
输出描述
输出一个整数,代表小明从起点到终点所花费的最小时间。
输入示例
7 9 1 2 1 1 3 4 2 3 2 2 4 5 3 4 2 4 5 3 2 6 4 5 7 4 6 7 9输出示例
12提示信息
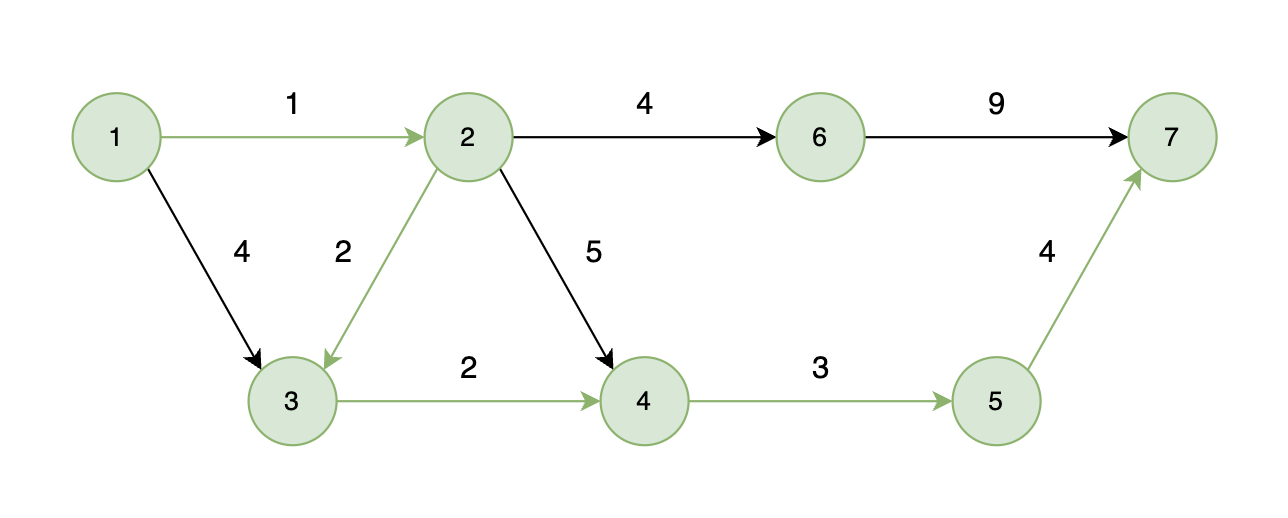
能够到达的情况:
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
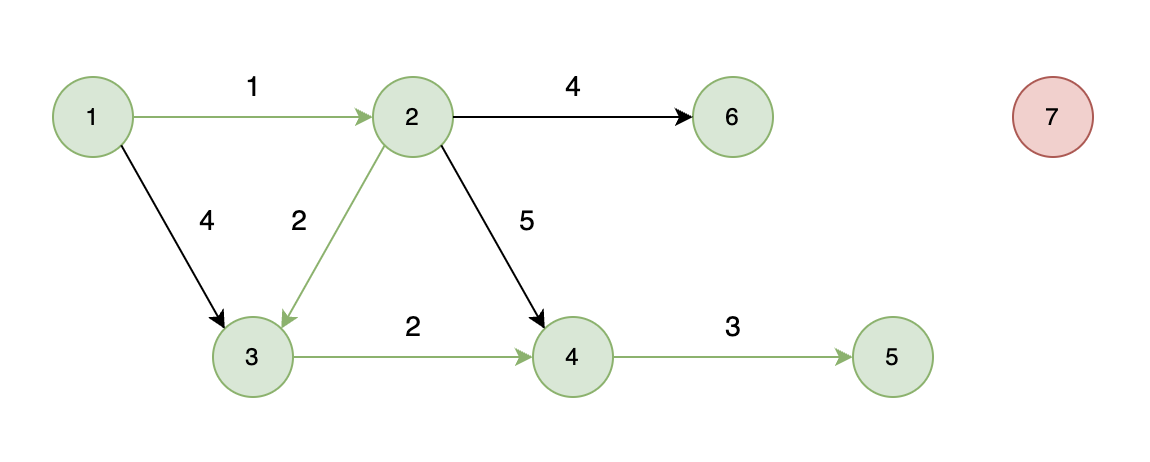
不能到达的情况:
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
数据范围:
1 <= N <= 500;
1 <= M <= 5000;
题解:朴素Dijkstra
注意:Dijkstra算法适用于没有负权重边的有向图。如果图中存在负权重边,则应该使用Bellman-Ford算法。
本题思路如下:
初始化图:
创建一个邻接矩阵grid,大小为n+1xn+1,所有值初始化为INT_MAX。
创建一个数组minDist,大小为n+1,所有值初始化为INT_MAX,除了start顶点,其值为0。
创建一个数组visited,大小为n+1,所有值初始化为false。
读取边信息:
对于m次循环:
读取p1, p2, val。
在grid中设置grid[p1][p2] = val。
Dijkstra算法:
初始化cur为-1,minVal为INT_MAX。
对于i从1到n:
找到未访问顶点中距离源点最近的顶点cur,更新minVal。
如果cur为-1,退出循环。
标记cur为已访问。
对于v从1到n:
如果v未被访问且grid[cur][v]不为INT_MAX:
如果minDist[cur] + grid[cur][v] < minDist[v],则更新minDist[v]。
输出结果:
如果minDist[end]为INT_MAX,则输出-1。
否则,输出minDist[end]。
基于以上思路,完整实现代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, m; // n为顶点数,m为边数
cin >> n >> m;
// 使用邻接矩阵表示图:顶点从1到n,初始化为无穷大(INT_MAX)
vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));
// 读取图的边信息
for (int i = 0; i < m; i++)
{
int p1, p2, val;
cin >> p1 >> p2 >> val;
// 由于是有向图,只需要设置一个方向的权重
grid[p1][p2] = val;
}
int start = 1; // 起始顶点
int end = n; // 终止顶点
// 初始化最短距离数组,所有顶点到源点的距离都设置为无穷大(除了源点本身)
vector<int> minDist(n + 1, INT_MAX);
minDist[start] = 0; // 源点到自身的距离为0
// 标记数组:标记顶点是否已访问 - 初始化为未访问
vector<bool> visited(n + 1, false);
// Dijkstra算法主循环,遍历所有顶点
for (int i = 1; i <= n; i++)
{
int minVal = INT_MAX; // 初始化当前最小距离为无穷大
int cur = -1; // 初始化当前顶点为 -1
// 找到未访问顶点中距离源点最近的顶点
for (int v = 1; v <= n; ++v)
{
if (!visited[v] && minDist[v] < minVal)
{
minVal = minDist[v]; // 更新最小距离
cur = v; // 更新当前顶点
}
}
if (cur == -1) // 如果没有找到这样的顶点,退出循环
break;
visited[cur] = true; // 标记该顶点已访问
// 更新相邻顶点的最短距离
for (int v = 1; v <= n; v++)
{
if (!visited[v] && grid[cur][v] != INT_MAX)
{
// 如果当前顶点到v顶点的距离加上当前顶点到源点的距离小于v顶点到源点的距离,则更新
if (minDist[cur] + grid[cur][v] < minDist[v])
minDist[v] = minDist[cur] + grid[cur][v];
}
}
}
// 输出结果,如果到end顶点的距离仍然是无穷大,则说明无法到达
if (minDist[end] == INT_MAX)
cout << -1 << endl;
else
cout << minDist[end] << endl; // 输出最短路径长度
}
本题是针对有向图,故对于每条边只需要存储单方向的信息;如果是无向图,就需要改进为双向处理,即:
grid[p1][p2] = val;
grid[p2][p1] = val;三、小结
后边打卡会在此之后补充优化后的Dijkstra算法,即使用优先队列(最小堆)的方式。今天的打卡到此结束,后边会继续加油!