第1题

在 Linux 系统终端中，以下哪个命令用于创建一个新的目录？(B)
A.newdir
B.mkdir
C.create
D.mkfold
解析：记住就行。

第2题

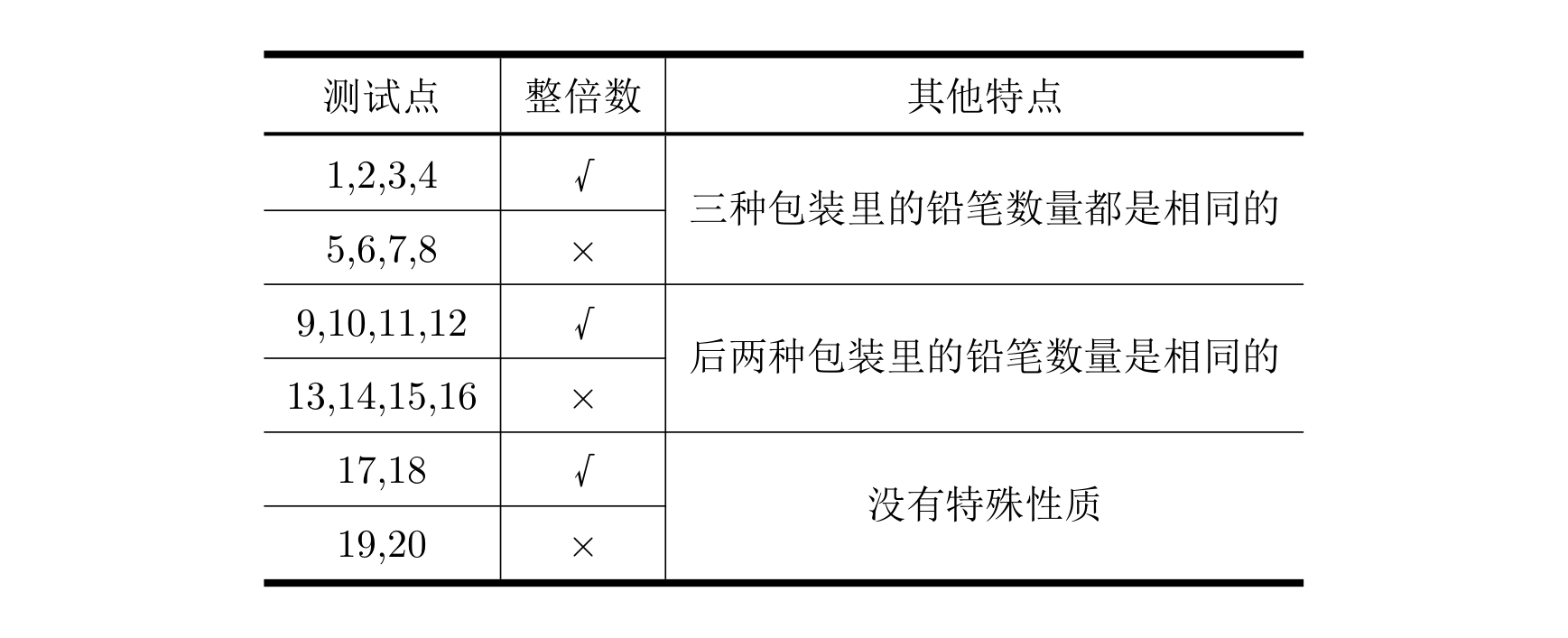
0,1,2,3,4 中选取 4 个数字，能组成（A）个不同四位数（注：最小的四位数是 1000 最大的四位数是 9999）。
A. 96
B. 18
C.120
D.84
解析：首位不能选0，所以方案数为$4\times 4\times 3\times 2=96$

第3题

假设 n 是图的顶点的个数，m 是图的边的个数，为求解某一问题有下面四种不同时间复杂度的算法。对于 m=Θ(n) 的稀疏图而言，下面的四个选项，哪一项的渐近时间复杂度最小(A)。
A. $O(m\sqrt{logn}\ast loglogn)$
B. $O(n^2+m)$
C. $O(\frac{n^2}{logm}+mlogn)$
D. $O(m+nlogn)$
解析：因为是稀疏图，所以可以把m和n看成相等的。接下来我们只需要看每个时间复杂度中最大的一个就行，所以可以直接排除B选项，接下来我们可以发现$\frac{n^2}{logm}$是一定比n要大的，所以我们又可以直接排除D选项，最后我们来比较C和A，不难发现，$\sqrt{logn}\ast loglogn$是一定小于$logn$的，并且选项C还带了一个分数，所以又可以把选项C排除，所以选A

第4题

假设有 n 根柱子，需要按照以下规则依次放置编号为 1,2,3,⋯ 的圆环：每根柱子的底 部固定，顶部可以放入圆环；每次从柱子顶部放入圆环时，需要保证任何两个相邻圆环的编号之和是一个完全平方数。请计算当有 4 根柱子时，最多可以放置（C）个圆环
A. 7
B.9
C.11
D.5
解析：第一个柱子放1，8；第二个柱子放2，7，9；第三个柱子放3，6，10；第四个柱子放4，5，11，总计11个，所以选C

第5题

以下对数据结构的表述不恰当的一项是：(B)
A. 队列是一种先进先出（FIFO）的线性结构
B.哈夫曼树的构造过程主要是为了实现图的深度优先搜索
C. 散列表是一种通过散列函数将关键字映射到存储位置的数据结构
D. 二叉树是一种每个结点最多有两个子结点的树结构
解析：哈夫曼树的构造过程是使用了的贪心算法，与dfs无关

第6题

以下连通无向图中，（A）一定可以用不超过两种颜色进行染色
A.完全三叉树
B.平面图
C.边双连通图
D.欧拉图
解析：三叉树只需要每一层染不同的颜色即可，如果是图，在遇到有环情况下，就有可能出事

第7题

最长公共子序列长度常常用来衡量两个序列的相似度。其定义如下：给定两个序列 $X=x1,x2,x3,\dots \dots ,x.$和$Y=y1,y2,y3,\dots \dots ,yn$，最长子序列最长公共子序列（LCS）问题的目标是找到一个最长的新序列$Z=z1,z2,z3,\cdots ,zk$​, 使得序列 Z 既是序列 X 的子序列，又是序列 Y 的子序列，且序列 Z 的长度 k 在满足上述条件的序列里是最大的。 （注：序列 A 是序列 B 的子序列，当且仅当在保持序列 B 元素顺序的情况下，从序列 B 中删除若干个元素，可以使得剩余的元素构成序列 A。）则序列 ABCAAAABA 和 ABABCBABA 的最长公共子序列长度为（C）
A.4
B.5
C.6
D.7
解析：直接找就行，不难发现是ABCABA

第8题

一位玩家正在玩一个特殊的掷骰子的游戏，游戏要求连续掷两次骰子，收益规则如下：玩家第一次掷出 x 点，得到 2x 元；第二次掷出 y 点，当 y=x 时玩家会失去之前得到的 2x 元而当 y≠x 时玩家能保住第一次获得的 2x 元。上述$x,y\in 1,2,3,4,5,6$。 例如：玩家第一次掷出 3 点得到 6 元后，但第二次再次掷出 3 点，会失去之前得到的 6 元，玩家最终收益为 0 元；如果玩家第一次掷出 3 点、第二次掷出 4 点，则最终收益是 6 元。假设骰子掷出任意一点的概率均为 1/6，玩家连续掷两次般子后，所有可能情形下收益的平均值是多少？(B)
A.7元
B.$\frac{35}{6}$元
C.$\frac{16}{3}$元
D.$\frac{19}{3}$元
解析：不难发现，前后两次是可以重复的，所以可以得到总共有$6\times 6=36$中可能，其中的收益分别是$10+20+30+40+50+60=210$元，所以平均值就是$\frac{210}{36}=\frac{35}{6}$

第9题

假设我们有以下的 C++ 代码：

bool res = a & b || c ^ b && a | c; 

请问，res 的值是什么？（A）
A.true
B.false
C.1
D.0
解析：首先可以直接排除C和D，然后又有我们知道，只要计算出来后的值大于0就是true，所以不难发现，KaTeX parse error: Expected 'EOF', got '&' at position 7: c ^ b &̲& a | c算出来的值大于0，所以res就是true

第10题

假设快速排序算法的输入是一个长度为n 的已排序数组，且该快速排序算法在分治过程总是选择第一个元素作为基准元素。以下哪个选项描述的是在这种情况下的快速排序行为?(C)
A. 快速排序对于此类输入的表现最好，因为数组已经排序。
B. 快速排序对于此类输入的时间复杂度是 $\Theta (nlogn)$。
C. 快速排序对于此类输入的时间复杂度是$\Theta (n^2)$。
D. 快速排序无法对此类数组进行排序，因为数组已经排序。
解析：只要快速排序遇到像这种和快排规矩一致的，那么时间复杂度就直接到达$\Theta (n^2)$。

第11题

以下哪个命令，能将一个名为 main.cpp 的 C++ 源文件，编译并生成一个名为 main 的可执行文件？（A）
A.g++ -o main main.cpp
B.g++ -o main.cpp main
C.g++ main -o main.cpp
D.g++ main.cpp -o main.cpp
解析：-o后面要放可执行文件，所以应该放main

第12题

在图论中，树的重心是树上的一个结点，以该结点为根时，使得其所有的子树中结点数最多的子树的结点数最少。一棵树可能有多个重心。请问下面哪种树一定只有一个重心？(C)
A.$4$个结点的树
B.$6$个结点的树
C.$7$个结点的树
D.$8$个结点的树
解析：给个规律：节点个数为偶数的树有两个重心，所以只能选C

第13题

如图是一张包含 6 个顶点的有向图，但顶点间不存在拓扑序。如果要删除其中一条边，使这 6 个顶点能进行拓扑排序，请问总共有多少条边可以作为候选的被删除边？（C）

A.1
B.2
C.3
D.4
解析：不难发现，有一个环（1，3，4），所以只要删去其中一条便就行，所以有3种可能。

第14题

A.10
B.11
C.12
D.13
f函数实在求十六进制下的各位数字之和（结果为十进制）要使其永远调用自身返回的是9，可以调用f(9)应为十六进制下9的各位数字之和是9，再反复调用还是9。但是题目要求是100(16) ~ 1A0(16)之间的数。
我们分情况考虑：也许它经过一次反复调用无法直接得到9，可能得到18，27，36…

1. 直接得到 9：108，117，126，135，144，153，162，171，180（9 个）
2. 得到 18 后再得到 9：189，198（2 个）
3. 得到 27 后在得到 9：（得不到，因为1A0，19F的各位数字之和都小于 27）

第15题

现在用如下代码来计算 $x^n$ ，其时间复杂度为（A）。

double quick_power(double x, unsigned n) {
	if (n == 0) return 1;
	if (n == 1) return x;
	return quick_power(x, n / 2)* quick_power(x, n / 2) * ((n & 1) ? x : 1);
}

A.$O(n)$
B.$O(1)$
C.$O(logn)$
D.$O(nlogm)$
解析：不难发现，这份代码不是快速幂，如果将递归的图画出来的话是一个满二叉树，所以是O(n)