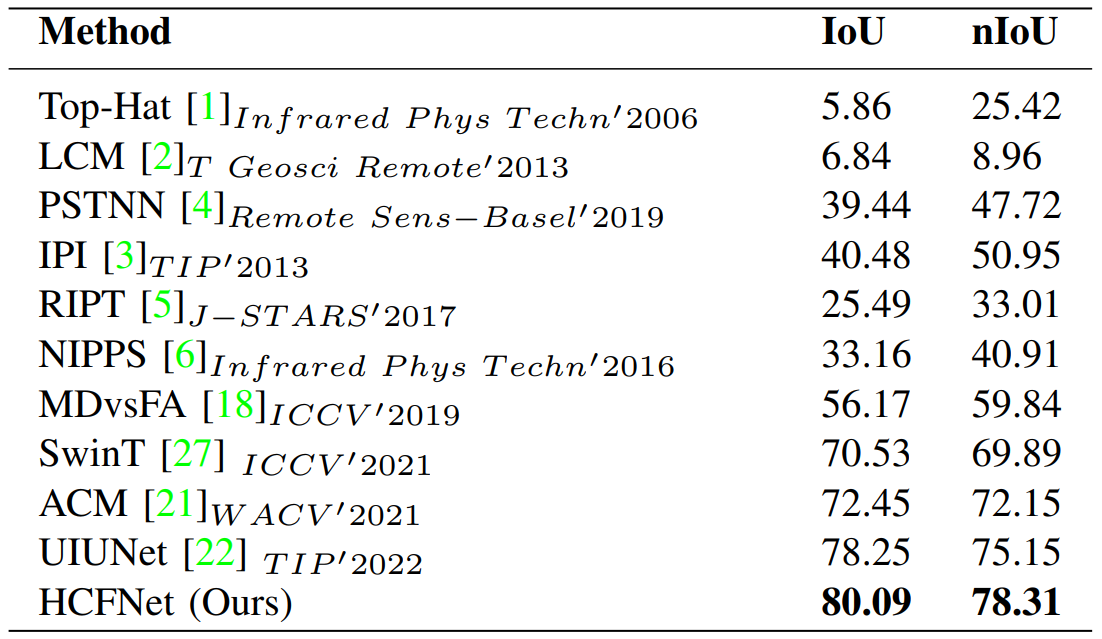
1.编写一个图像二维卷积程序。它应该能够处理任何灰度输入图像，并使用以下内核进行操作：

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
import random as rm
import math
import cv2

# import and show the image
img = cv2.imread('einstein.png',cv2.IMREAD_GRAYSCALE)
plt.imshow(img,plt.cm.gray)
print(img)
img_sz=img.shape

代码逻辑：
提取灰度图，显示图片

def pascal(k,n):
    if k >= 0 and k <= n:
        y = math.factorial(n)/(math.factorial(n-k)*math.factorial(k))
    else:
        y=0
    return y

算组合种类的pascal函数，就是数学里的大C，之后用于计算索贝尔算子

2.索贝尔算子

Sobel 算子（Sobel Operator） 是一种常用的 边缘检测 算法，用于图像处理领域。它通过计算图像像素的梯度（变化率）来检测图像中的边缘。具体来说，Sobel 算子用于确定图像中灰度变化最明显的区域，这些区域通常对应于物体的边界或细节。
在二维函数中，计算梯度，可以找到变化率最大的部分来，索贝尔算子就是在图像中计算梯度最大的部分。他有两种3*3的卷积核（滤波器）
分别是：

def sobel(order): 
    sobel_x=np.zeros([order,order])
    smooth=np.zeros([order,1])
    diff=np.zeros([order,1])
    for j in range(0,order):
        smooth=pascal(j,order-1)
#         print(smooth)
        for k in range(0,order):
            diff=pascal(k,order-2)-pascal(k-1,order-2)
#             print(diff)
            sobel_x[j][k]=smooth*diff
            
    sobel_y=-1*sobel_x.T
    return sobel_x,sobel_y

这个代码就可以生成order*order的两种索贝尔算子，如果order是3，那么上面的索贝尔算子就是上面那个图。

# convolution for sobel kernel, 2 kernel in 2 directions
def convolution_2(img,kernel1,kernel2):
    sz_img=img.shape
    sz_kernel=kernel1.shape
    #[a,b]=sz_kernel
    
    a=int((sz_kernel[0]-1)/2)
    b=int((sz_kernel[1]-1)/2)
    
    pimg=np.zeros(sz_img)
    for j in range(a,(sz_img[0]-a)):
        for k in range(b,(sz_img[1]-b)):
            for i in range(0,2):
                ximg=np.sum(img[j-a:j+a+1,k-b:k+b+1]*kernel1)
                yimg=np.sum(img[j-a:j+a+1,k-b:k+b+1]*kernel2)
                pimg[j][k]=np.abs(ximg)+np.abs(yimg)
    
    return pimg            

代码逻辑：
举个例子，现在有一个55的图片，你的卷积核是33的，那么现在你需要做的是，在55的图片中先取最左上角的33矩阵和两个卷积核相卷积，然后得出两个数字，给这两个数字都做一次绝对值然后再相加，就是这个点的近似梯度，然后55的图像考虑边缘，能做33次这样的操作，最后得到3*3的矩阵。
理论上求该点的平方和然后开方才应该是这个点的真实梯度，为什么要用绝对值和呢，因为在庞大的计算中，如果都去做平方和，那就太耗费系统资源了，所以使用绝对值和是近似的计算方法，忽略了方向性，只看水平和垂直梯度的绝对强度之和，它可以提供相对较强的边缘信息，但缺少准确性，边缘会显得比较尖锐和不平滑。

# when mask size is 3, ploting the Sobel kenerl processed image
[sobel_x,sobel_y]=sobel(3)
print(sobel_x,'\n',sobel_y)
sobel_img = convolution_2(img,sobel_x,sobel_y)
#sobel_x_img=np.uint8(sobel_x_img)
plt.imshow(sobel_img,plt.cm.gray)
# print(sobel_x_img)

计算卷积，生成边缘图像

3.高斯核与高斯卷积

def convolution_1(img,kernel1):
    sz_img = img.shape          # 获取图像的尺寸
    sz_kernel = kernel1.shape    # 获取卷积核的尺寸
    a = int((sz_kernel[0]-1)/2)  # 计算卷积核在 x 方向的半径
    b = int((sz_kernel[1]-1)/2)  # 计算卷积核在 y 方向的半径
    
    pimg = np.zeros(sz_img)      # 初始化输出图像的大小，和原图大小相同
    for j in range(a, (sz_img[0]-a)):      # 遍历图像的每一个像素
        for k in range(b, (sz_img[1]-b)):
            # 从原图像中提取出一个与高斯核大小相同的子矩阵，进行逐元素相乘并累加
            ximg = np.sum(img[j-a:j+a+1, k-b:k+b+1] * kernel1)
            pimg[j][k] = np.abs(ximg)     # 将卷积后的结果的绝对值赋值给输出图像
    return pimg

这个代码是卷积的定义操作，高斯核还没进去

#kernel
#gaussian
def gaussian(x,y,delta):
    return 1/(2*math.pi*delta**2)*np.exp(-1*(x*x+y*y)/(2*delta**2))
def Gau(order):
    delta=0.3*((order-1)/2-1)+0.8
    a=int((order-1)/2)
    ga=np.zeros([order,order])
    for j in range(-a,a+1):
        for k in range(-a,a+1):
            ga[j][k]=gaussian(j,k,delta)
    
    return ga
# ga1=1/16*np.array([[1,2,1],[2,4,2],[1,2,1]])
# ga2=1/159*np.array([[2,4,5,4,2],[4,9,12,9,4],[5,12,15,12,5],[4,9,12,9,4],[2,4,5,4,2]])

高斯核（Gaussian Kernel）是图像处理中一种常用的滤波器，用于平滑图像，消除噪声。它是根据高斯函数定义的二维矩阵。高斯核的作用是将图像中的每个像素与其邻域像素的加权平均计算，权重依据高斯分布确定，离中心越近的像素权重越大，离得越远的像素权重越小。
卷积后的图像会变得更加平滑，噪声被抑制，同时保留主要的图像特征。这个函数中使用了 绝对值，通常用于保持结果的非负性，但在一般高斯卷积中不一定需要绝对值。
代码先定义了高斯函数，然后定义了高斯核。并给出了常见的三阶高斯核和五阶高斯核
ga1 是较小的高斯核，平滑效果相对较弱，但保留了更多的图像细节。
ga2 是较大的高斯核，平滑效果较强，适合噪声较大的图像。

# when mask size is 3, ploting the Gaussian kenerl processed image
ga1=Gau(3)
print(ga1)
gaussian_img = convolution_1(img,ga1)
#sobel_x_img=np.uint8(sobel_x_img)
plt.imshow(gaussian_img,plt.cm.gray)
#print(sobel_x_img)

这个代码就是对图像进行高斯卷积操作模糊边缘，高斯卷积核为三层高斯核

效果如下，如果用九阶高斯核代码和输出如下：

# when mask size is 9, ploting the Gaussian kenerl processed image
ga2=Gau(9)
print(ga2)
gaussian_img = convolution_1(img,ga2)
#sobel_x_img=np.uint8(sobel_x_img)
plt.imshow(gaussian_img,plt.cm.gray)
#print(sobel_x_img)

4.Haar小波卷积核

Haar 小波卷积 是一种高效的边缘检测和特征提取方法。它通过简单的 1 和 -1 构造出卷积核，可以快速检测图像中的边缘和变化。
卷积操作 将 Haar 核应用于图像，生成新的特征图，用于分析图像的结构和特征。
Haar 小波广泛应用于 边缘检测、图像压缩 和 特征提取 等任务，尤其适合实时计算和高效处理场景。
在计算机视觉中，Haar 小波常用于特征提取。例如，人脸检测算法中，Haar 特征被用于快速检测图像中的人脸区域。适合实时计算和高效处理场景。
与 Sobel 核的对比
Sobel 卷积核也是用于边缘检测的，但与 Haar 核不同，Sobel 核使用的是平滑的梯度变化，而 Haar 核直接检测的是 1 和 -1 的急剧变化。与 Sobel 核相比，Haar 核的计算更加简单，但 Sobel 核能够更精细地检测梯度信息，适合检测较为平滑的边缘。

# Haar kernel
def Haar(order):
    block=np.ones([order,order]).astype(int)
    mask1=np.concatenate([-1*block,block],axis=0)
    mask2=np.concatenate([-1*block,block],axis=1)
    mask3=np.concatenate([block,-1*block,block],axis=0)
    mask4=np.concatenate([block,-1*block,block],axis=1)
    mask5=np.concatenate([mask1,-1*mask1],axis=1)
    mask=[mask1,mask2,mask3,mask4,mask5]
    return mask

# 2D convolution for Haar kernel
def convolution_3(img,mask):
    sz_img=img.shape
    sz_kernel=mask.shape
    #[a,b]=sz_kernel
    
    a=int(sz_kernel[0])
    b=int(sz_kernel[1])
    
    pimg=np.zeros(sz_img)
    for j in range(0,(sz_img[0]-a)):
        for k in range(0,(sz_img[1]-b)):
            for i in range(0,2):
                ximg=np.sum(img[j:j+a,k:k+b]*mask)
                #yimg=np.sum(img[j-a:j+a+1,k-b:k+b+1]*kernel2)
                pimg[j][k]=np.abs(ximg)
    
    return pimg

代码逻辑：
定义Haar卷积核，注意，给定一个维度数，会同时产生五个Haar卷积核，存放在数组中
mask1: 检测 水平边缘，例如物体的上下轮廓。
mask2: 检测 垂直边缘，例如物体的左右轮廓。
mask3: 检测 正对角线方向，捕捉从左上到右下的边缘。
mask4: 检测 反对角线方向，捕捉从左下到右上的边缘。
mask5: 检测 复杂变化，这是由 mask1 的进一步组合生成的更复杂卷积核，通过在水平和垂直方向进行进一步拼接。这种结构的卷积核可以检测图像中的 更复杂的变化模式，包括一些图像块内部的细节变化。它的作用不是单一的某个方向检测，而是组合式的模式检测，能捕捉图像中的更细腻特征。

# when mask size is 1, ploting the Haar kenerl processed image
mask=Haar(1)
print(mask)
for ma in mask:
    Haar_img = convolution_3(img,ma)
    plt.imshow(Haar_img,plt.cm.gray)
    plt.show()

# when mask size is 2, ploting the Haar kenerl processed image
mask=Haar(2)
print(mask)
for ma in mask:
    Haar_img = convolution_3(img,ma)
    plt.imshow(Haar_img,plt.cm.gray)
    plt.show()

这个代码就是使用Haar的两个不同的size输出的效果。
结果就是Sobel 核提取图像的边缘；高斯核使图像模糊；不同的 Haar mask 效果不同。Type1 的输出像 sobel 一样提取边缘。Type2 的输出像高斯一样使图像模糊。Type3 看起来像是 type1 中 2 个输出的组合。
核的尺寸越大，核的效果越强。