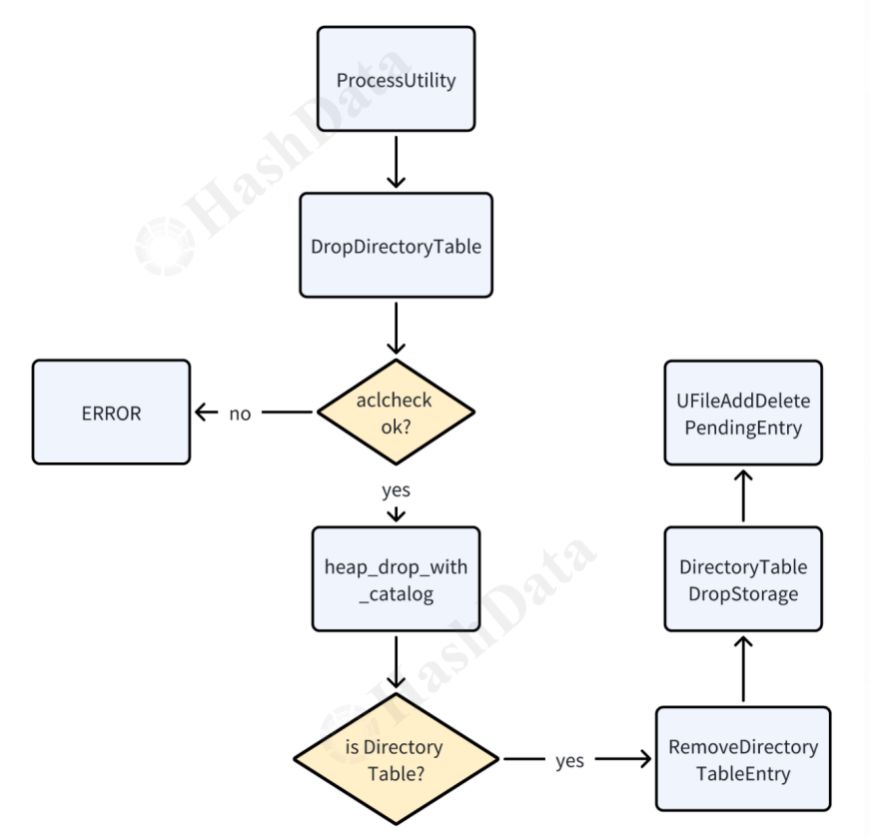
研究D的处理效应，找一个相似的样本，他们的差异就是处理效应。但：难点就在如何找到相似的样本。那么就通过合成法来合成一个虚拟的重庆。

案例：美国加州香烟法案出台

依靠权重来合成一个新的y

• 假设我们不用SCM，直接靠着线性趋势外推的方式，似乎简单的能得到政策效果。但是存在的质疑：

• 数据的起点该怎么选？选1970？1977？还是其他？
  

• DID的思想
  1983-1988年似乎满足平行趋势，假设20包，在对其他州减去20包，形成加州的反事实，在减去真实的加州的值，就是政策效应。
  局限：

• 这是只有加州一个样本，无法做统计检验。

• 人为干预选取的1983-1988样本点才满足平行趋势，再往前推一点，就不满足了，那么结论的稳健性呢（比如用1977-1983），也不能满足？
  
  结论，从实验结果来看，线性趋势外推、DID与SCM的估计结果差别大不

SCM合成控制法

• 用pre的38个样本，加权$y^{C{A}^{\prime }}$使得与$Y^{CA}$完美重合。
• 其实，与加州相似（GDP接近，地理位置接近…）的洲权重越大，不相似的越小。
• post后的距离差就是政策效果。
  

合成结果

两者很接近，表明合成结果很好

权重结果

• 注意，单个个体的权重，一定不能太大，否则结果可能出现偏误（估计过大过小）。一般权重（不超过0.5）太大，太大就删掉，再重新估计。
  

最重要的图形分析

• 此图就是合成的差值相减得到的。

• pre前，趋于0
• post后，表现出差异，越大越好（与0的距离越大）

检验（头发图）

• 安慰剂检验
  就是对其他的州也进行与CA相似的合成控制法，画得下图。
  如果CA的线与其他的线，差别不大的话，那么就有问题了（红色）。
  如果CA的与其他的线，差别很大，结论ok（黑色）。

第一次：做38次，38个州，

去掉在pre阶段合成不好的州

第二次：34次，剩下34个州

第三次：29次，剩下29个州

第四次：19次，剩下19个州

此时的结果比较好了

理论

反事实架构的建立

估算方法

因子模型解释

• ${\delta }_i$,控制共同的时间趋势。
• ${\lambda }_t\ast {\mu }_i$,考虑到每个州都有自己的时间趋势，加上一个变系数$\mu$，或者叫异质性。
• ${\theta }_t{Z}_i$,控制变量的 $Z$取的是时间的平均值，没有下标$t$。
  机器学习的局限：解释变量的个数不多，不好整，并且解释变量在时间维度也有趋势，也不好整。

A、B、C部分的期望，理论上都为0

模型评估

• 指标为MSPE
• 事前小（合成误差越小越好），事后大（政策效果明显）
• 或者用RMSPE（MSPE开根号）

stata演示-代码

• 画图 最初的样子
  
  #d ;表示告诉stata 看到;换行
  #d cr表示告诉stata 看到cr换行
  
• 画黑白图的代码
  
• 补充一点：尽量把控制组的ID设成1，为了后面的for语句好写。
  

合成控制的代码

• 为何要加y的滞后项？
• 因为可以使得pre阶段的两条线越接近
  trunit(3):CA的ID是3，是实验组
  trperiod(1989):政策开始的时点，注意，有些政策是1989年6月以后，取1989，反之去1988年。但也不一定，也要根据研究目的来定。【开通高铁的例子】
  

xperiod(1980(1)1988):公共变量（比如lnincome、retprice）的样本期

• 通常我们做的pre线是波动大，差异大的，这时就需要调整。尽量多加一些解释变量，然后再适当调整，似乎带有一些凑的成分。
• fig 是否画图
• nested 模型结果计算优化命令
• allopt 模型结果计算优化命令【但结果很慢】

table、fig结果

注意命令keep('result')

• 调入内存，查看权重table2、以及table1的值。图3
• SCM核心的几部分结果都可以根据上面的代码进行计算了。
  

组合检验（permutation test）-算MSPE

• 算MSPE
  

安慰剂检验

• 问题，不同的州（个体）有不同的特征，那么都按实验组的特征（当解释变量）是否对其他的个体（公平）？
• 不合适，常见的想法：尽可能 多家解释变量，用Lasso的方式挑选出变量。
  

• 这里执行的是39个部分的安慰剂检验。

• 数据合并
  
• 画图

• 介绍一下经验P值

（不依靠分布，就是一个频率近似替代概率）

• 关于此问题（加州禁烟令）的假设检验问题
  
• 代码
  
• 结果
  
• 关于论文安慰剂检验中，如何出掉“分叉”的州，即fig5怎么来的。
  
  keep if MSPE>20*MSPE3这里调节倍数
• 续上张图
  

levelsof命令：列出非重复的数的ID

• 思考：关于安慰剂检验的诟病
• 文章在安慰剂检验中，删掉20、10、4州等，他没有根据~，为啥不删除21、9、3呢？加入人为干预，缺失一定标准。
• 办法：在每一个州加上一个自己的MSPE。相当于一个加权惩罚迭代。

推断平均政策效果

论文图8
为了回避安慰剂检验的诟病，作者从总体的角度去进一步说明平均的政策效应。
就是看MSPE的前后Ratio比。图中可以发现，大部分都集中在[0，3]左右，差异是比较小的，但是我们的CA，差异最大。特别明显。

总结

• 如何确定control组的，如何选取赶紧的Donor pool
• 关于Z（控制）的选择，很重要，本文的随意性很大，目的都是为了调整pre线完全融合，$MSP{E}_{pre}$近似为0