目录
110.字符串接龙
思路
方法一: 广搜
105.有向图的完全可达性
思路
1.确认递归函数,参数
2.确认终止条件
3.处理目前搜索节点出发的路径
方法一:广搜
106.岛屿的周长
思路
解法一:
解法二:
方法一
方法二
110.字符串接龙
- 题目链接:卡码网题目链接(ACM模式)
文章讲解:代码随想录
字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列:
序列中第一个字符串是 beginStr。
序列中最后一个字符串是 endStr。
每次转换只能改变一个字符。
转换过程中的中间字符串必须是字典 strList 中的字符串。
给你两个字符串 beginStr 和 endStr 和一个字典 strList,找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列,返回 0。
输入描述
第一行包含一个整数 N,表示字典 strList 中的字符串数量。 第二行包含两个字符串,用空格隔开,分别代表 beginStr 和 endStr。 后续 N 行,每行一个字符串,代表 strList 中的字符串。
输出描述
输出一个整数,代表从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量。如果不存在这样的转换序列,则输出 0。
输入示例
6 abc def efc dbc ebc dec dfc yhn输出示例
4
提示信息
从 startStr 到 endStr,在 strList 中最短的路径为 abc -> dbc -> dec -> def,所以输出结果为 4
数据范围:
2 <= N <= 500
思路
以示例1为例,从这个图中可以看出 abc 到 def的路线 不止一条,但最短的一条路径上是4个节点。

本题只需要求出最短路径的长度就可以了,不用找出具体路径。
所以这道题要解决两个问题:
- 图中的线是如何连在一起的
- 起点和终点的最短路径长度
首先题目中并没有给出点与点之间的连线,而是要我们自己去连,条件是字符只能差一个。
所以判断点与点之间的关系,需要判断是不是差一个字符,如果差一个字符,那就是有链接。
然后就是求起点和终点的最短路径长度,这里无向图求最短路,广搜最为合适,广搜只要搜到了终点,那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。
本题如果用深搜,会比较麻烦,要在到达终点的不同路径中选则一条最短路。 而广搜只要达到终点,一定是最短路。
另外需要有一个注意点:
- 本题是一个无向图,需要用标记位,标记着节点是否走过,否则就会死循环!
- 使用set来检查字符串是否出现在字符串集合里更快一些
方法一: 广搜
from typing import List
from collections import deque
class Solution:
def __init__(self) -> None:
pass
# 判断两个字符串是否只有一个不相同的字符
def judge(self,s1:str,s2:str):
count = 0
for i in range(len(s1)):
if s1[i] != s2[i]:
count += 1
return count == 1
def find_shortest_path(self,startStr:str,endStr:str,wordsList:List,n:int) -> int:
if startStr == endStr :
return 0
visited = [False for _ in range(n)]
que = deque()
que.append((startStr,1))
while que:
compare_str,step = que.popleft()
# 判断与结束字符串是否相差一个字符,如果是就已经找到了最短路径
if self.judge(compare_str,endStr):
return step + 1
# 循环遍历数组,首先与startStr比较,找到相差一个字符的,加入队列
# 然后再循环剩下未访问的字符,与队列的字符串比较是否相差一个字符
for i in range(n):
if not visited[i] and self.judge(wordsList[i],compare_str):
visited[i] = True
que.append((wordsList[i],step+1))
return 0
def main():
n = int(input())
startStr,endStr = input().split()
wordList = []
for i in range(n):
wordList.append(input().strip())
res = Solution()
print(res.find_shortest_path(startStr,endStr,wordList,n))
if __name__ == "__main__":
main()105.有向图的完全可达性
- 题目链接:卡码网题目链接(ACM模式)
文章讲解:代码随想录
【题目描述】
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,...,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
【输入描述】
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
【输出描述】
如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
【输入示例】
4 4 1 2 2 1 1 3 2 4【输出示例】
1
【提示信息】
从 1 号节点可以到达任意节点,输出 1。
数据范围:
- 1 <= N <= 100;
- 1 <= K <= 2000。
思路
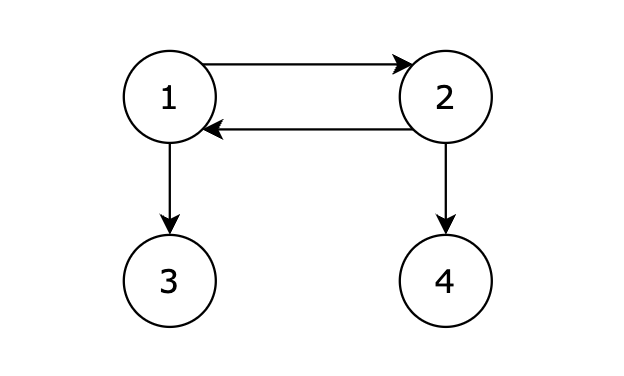
本题给我们是一个有向图, 意识到这是有向图很重要!
接下来我们再画一个图,从图里可以直观看出来,节点6 是 不能到达节点1 的

这就很容易让我们想起岛屿问题,只要发现独立的岛,就是不可到达的。
但本题是有向图,在有向图中,即使所有节点都是链接的,但依然不可能从0出发遍历所有边。
例如上图中,节点1 可以到达节点2,但节点2是不能到达节点1的。
所以本题是一个有向图搜索全路径的问题。 只能用深搜(DFS)或者广搜(BFS)来搜。
以下dfs分析 大家一定要仔细看,本题有两种dfs的解法,很多题解没有讲清楚。 看完之后 相信你对dfs会有更深的理解。
深搜三部曲:
1.确认递归函数,参数
需要传入地图,需要知道当前我们拿到的key,以至于去下一个房间。
同时还需要一个数组,用来记录我们都走过了哪些房间,这样好知道最后有没有把所有房间都遍历的,可以定义一个一维数组。
2.确认终止条件
遍历的时候,什么时候终止呢?
这里有一个很重要的逻辑,就是在递归中,我们是处理当前访问的节点,还是处理下一个要访问的节点。
这决定 终止条件怎么写。
首先明确,本题中什么叫做处理,就是 visited数组来记录访问过的节点,该节点默认 数组里元素都是false,把元素标记为true就是处理 本节点了。
如果我们是处理当前访问的节点,当前访问的节点如果是 true ,说明是访问过的节点,那就终止本层递归,如果不是true,我们就把它赋值为true,因为这是我们处理本层递归的节点。
代码就是这样,提供C++写法:
// 写法一:处理当前访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
if (visited[key]) {
return;
}
visited[key] = true;
list<int> keys = graph[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(graph, key, visited);
}
}
如果我们是处理下一层访问的节点,而不是当前层。那么就要在 深搜三部曲中第三步:处理目前搜索节点出发的路径的时候对 节点进行处理。
这样的话,就不需要终止条件,而是在 搜索下一个节点的时候,直接判断 下一个节点是否是我们要搜的节点。
代码就是这样的,提供C++写法:
// 写法二:处理下一个要访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
list<int> keys = graph[key];
for (int key : keys) {
if (visited[key] == false) { // 确认下一个是没访问过的节点
visited[key] = true;
dfs(graph, key, visited);
}
}
}
可以看出,如何看待 我们要访问的节点,直接决定了两种不一样的写法,很多录友对这一块很模糊,可能做过这道题,但没有思考到这个维度上。
3.处理目前搜索节点出发的路径
其实在上面,深搜三部曲 第二部,就已经讲了,因为终止条件的两种写法, 直接决定了两种不一样的递归写法。
这里还有细节:
看上面两个版本的写法中, 好像没有发现回溯的逻辑。
我们都知道,有递归就有回溯,回溯就在递归函数的下面, 那么之前我们做的dfs题目,都需要回溯操作,例如:0098.所有可达路径, 为什么本题就没有回溯呢?
代码中可以看到dfs函数下面并没有回溯的操作。
此时就要在思考本题的要求了,本题是需要判断 1节点 是否能到所有节点,那么我们就没有必要回溯去撤销操作了,只要遍历过的节点一律都标记上。
那什么时候需要回溯操作呢?
当我们需要搜索一条可行路径的时候,就需要回溯操作了,因为没有回溯,就没法“调头”, 如果不理解的话,去看我写的 0098.所有可达路径 的题解。
方法一:广搜
import collections
path = set() # 纪录 BFS 所经过之节点
def bfs(root, graph):
global path
que = collections.deque([root])
while que:
cur = que.popleft()
path.add(cur)
for nei in graph[cur]:
que.append(nei)
graph[cur] = []
return
def main():
N, K = map(int, input().strip().split())
graph = collections.defaultdict(list)
for _ in range(K):
src, dest = map(int, input().strip().split())
graph[src].append(dest)
bfs(1, graph)
if path == {i for i in range(1, N + 1)}:
return 1
return -1
if __name__ == "__main__":
print(main())
106.岛屿的周长
- 题目链接:卡码网题目链接(ACM模式)
文章讲解:代码随想录
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。
你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿,假设组成岛屿的陆地边长都为 1,请计算岛屿的周长。岛屿内部没有水域。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的周长。
输入示例
5 5 0 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 1 1 0 0 0 0 0 0输出示例
14
提示信息
岛屿的周长为 14。
数据范围:
1 <= M, N <= 50。
思路
岛屿问题最容易让人想到BFS或者DFS,但本题确实还用不上。
为了避免大家惯性思维,所以给大家安排了这道题目。
解法一:
遍历每一个空格,遇到岛屿则计算其上下左右的空格情况。
如果该陆地上下左右的空格是有水域,则说明是一条边,如图:

陆地的右边空格是水域,则说明找到一条边。
如果该陆地上下左右的空格出界了,则说明是一条边,如图:
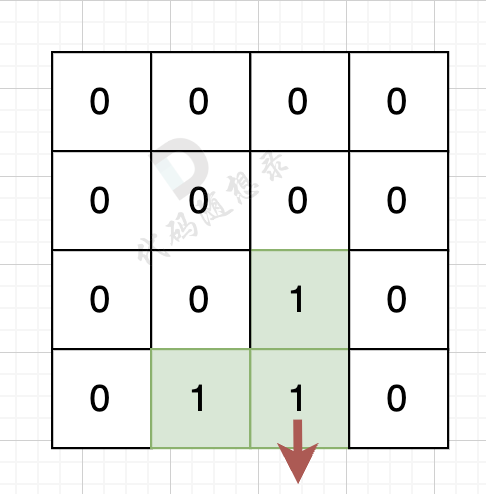
该陆地的下边空格出界了,则说明找到一条边。
解法二:
计算出总的岛屿数量,总的变数为:岛屿数量 * 4
因为有一对相邻两个陆地,边的总数就要减2,如图红线部分,有两个陆地相邻,总边数就要减2
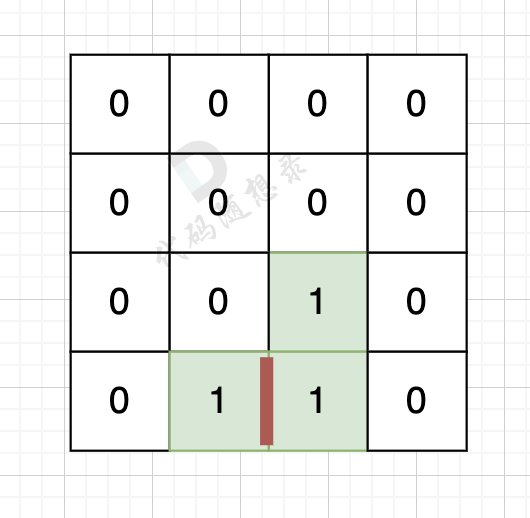
那么只需要在计算出相邻岛屿的数量就可以了,相邻岛屿数量为cover。
结果 result = 岛屿数量 * 4 - cover * 2;
方法一
directions = [[0,1],[1,0],[0,-1],[-1,0]]
count = 0
def calculate_sides(grid,x,y):
global count
for i,j in directions:
next_x = x + i
next_y = y + j
if next_x < 0 or next_x >= len(grid) or next_y < 0 or next_y >= len(grid[0]) or grid[next_x][next_y] == 0:
count += 1
def main():
n,m = map(int,input().split())
grid = []
for i in range(n):
grid.append(list(map(int,input().split())))
global count
for i in range(n):
for j in range(m):
if grid[i][j] == 1:
calculate_sides(grid,i,j)
print(count)
if __name__ == "__main__":
main()方法二
directions = [[0,1],[1,0],[0,-1],[-1,0]]
def main():
n,m = map(int,input().split())
grid = []
for i in range(n):
grid.append(list(map(int,input().split())))
sum = 0
cover = 0
for i in range(n):
for j in range(m):
if grid[i][j] == 1:
sum += 1
if i - 1 >= 0 and grid[i-1][j] == 1: cover += 1
if j - 1 >= 0 and grid[i][j-1] == 1: cover += 1
print(sum * 4 - cover * 2)
if __name__ == "__main__":
main()