目录

Δ前言

一、链表中特定值结点的删除

        0.题目：

        1.算法设计思想：

        2.C语言描述：

        3.算法的时间和空间复杂度：

二、链表链表最小值结点的删除

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

三、链表的头插法

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

四、链表的尾插法

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

五、链表的逆置

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

六、链表中特定区间元素的删除

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

七、找出两个链表的公共结点

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

八、链表奇偶位序元素的分离

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

九、链表奇偶位序元素的分离但一个头插一个尾插

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

十、链表的去重

        0.题目 : 

        1.算法设计思想 : 

        2.C语言描述 : 

        3.算法的时间和空间复杂度 : 

Δ总结

---

Δ前言

• 从408应试的角度来看，算法题主要分为四部分——①线性表(包括数组和链表)；②二叉树；③图；④查找。本篇博文主要讲链表相关的基础算法（由于链表相关的算法题目较多，所以up分为了上下两篇博文）。
• 博文中涉及到的题目全部参考自《王道数据结构考研复习指导》和《竟成408考研复习全书》。
• 注意事项——①点击文章侧边栏目录或者文章开头的目录可以进行跳转。②所有题目都符合408算法题的题目格式，即第一问算法设计思想、第二问C语言描述该算法、第三问计算该算法的时空复杂度。
• 良工不示人以朴，up所有文章都会适时补充完善。大家如果有问题都可以在评论区进行交流或者私信up。感谢阅读！

---

一、链表中特定值结点的删除

        0.题目：

        在一个带有头结点的单链表中，要求删除所有值为e的结点(假设结点中的数据类型是int类型，值为e的结点不唯一)，请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想：

        这道题目的本质，其实就是单链表结点的删除。只不过一般涉及到单链表元素删除都是按照位序或者下标来删除，而每个位序或者下标对应的元素都是唯一的。而此题要求按照值来删除元素，每个值对应的元素不一定是唯一的。

        所以，肯定要先遍历链表，up这里使用while循环来实现，而在遍历链表的同时，还需要增设一个if条件语句，用于判断当前结点是否满足删除的条件，如果满足就把它干了，如果不满足就继续往下找，什么时候链表遍历完了，咱就撤了。

        那么，如果满足条件，到底怎么删呢？

        嗯，要删除当前结点，逻辑上很简单，就是先找到当前结点的前一个结点，比方说q指向当前结点，p指向q的前一个结点，只需“p->next = q->next;”就彳亍了，但由于链表是动态分配内存，所以肯定要有一个临时的指针变量q来指向被删除的元素，这样就可以调用free函数把这片空间释放掉。

        2.C语言描述：

                完整代码如下：(注意看注释)

# include <stdio.h>
# include <stdlib.h>    //<stdlib.h> 是标准库的一部分，包含了 malloc、free 等动态内存分配函数

//定义数据结构
typedef struct LinkNode{
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//函数声明
void initialize(LinkList * pHead);          //二级指针，确保修改的就是统一指针变量
LinkNode * createNode(int data);
void freeList(LinkNode * pHead);
void traverse(LinkList pHead);
int deleteByValue(LinkList pHead, int e);

int main(void) {
    LinkList pHead = NULL;
    initialize(&pHead);

    //给出一个链表，用于测试该算法。
    LinkNode * a1 = createNode(1);
    LinkNode * a2 = createNode(5);
    LinkNode * a3 = createNode(11);
    LinkNode * a4 = createNode(5);
    LinkNode * a5 = createNode(100);

    pHead->next = a1;
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;
    a5->next = NULL;
    
    printf("删除元素前链表情况如下——\n");
    traverse(pHead);

    int count = deleteByValue(pHead, 5);
    printf("\n链表中被删除的值为5的结点一共有%d个~\n\n",count);
    printf("删除元素后链表情况如下——\n");
    traverse(pHead);
    freeList(pHead);

    return 0;
}

//初始化链表的算法，形参列表为链表的头指针。
void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode * )malloc(sizeof(LinkNode));
    (*pHead)->next = NULL;
    (*pHead)->data = 0;
}

/**
    function : create a new LinkNode(as its name)
    parameter list : (1) data---the wished data in the new LinkNode
 */
LinkNode * createNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

/**
    function : traverse the linkedlist(as its name)
    parameter list : (1) pHead---the head pointer of the operated linkedlist
 */
void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;
    while (p != NULL) {
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
}

/**
    function : free the specific given linkedlist
    parameter list : pHead---the head pointer of the operater linkedlist
 */
void freeList(LinkNode * pHead) {
    if (pHead == NULL) return;

    LinkNode * p = pHead;
    LinkNode * temp;
    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}


//实现“删除链表中特定值的结点”算法的核心方法
int deleteByValue(LinkList pHead, int e) {
    int count = 0;          //count变量用于记录被删除的结点的个数
    LinkNode * q = NULL;    //临时指针变量q/* 
    2024.8.8 星期三
    Day1———Delete the Nodes of certain value in a linkedlist
 */
# include <stdio.h>
# include <stdlib.h>    //<stdlib.h> 是标准库的一部分，包含了 malloc、free 等动态内存分配函数

//定义数据结构
typedef struct LinkNode{
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//函数声明
void initialize(LinkList * pHead);          //二级指针，确保修改的就是统一指针变量
LinkNode * createNode(int data);
void freeList(LinkNode * pHead);
void traverse(LinkList pHead);
int deleteByValue(LinkList pHead, int e);

int main(void) {
    LinkList pHead = NULL;
    initialize(&pHead);

    //给出一个链表，用于测试该算法。
    LinkNode * a1 = createNode(1);
    LinkNode * a2 = createNode(5);
    LinkNode * a3 = createNode(11);
    LinkNode * a4 = createNode(5);
    LinkNode * a5 = createNode(100);

    pHead->next = a1;
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;
    a5->next = NULL;
    
    printf("删除元素前链表情况如下——\n");
    traverse(pHead);

    int count = deleteByValue(pHead, 5);
    printf("\n链表中被删除的值为5的结点一共有%d个~\n\n",count);
    printf("删除元素后链表情况如下——\n");
    traverse(pHead);
    freeList(pHead);

    return 0;
}

//初始化链表的算法，形参列表为链表的头指针。
void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode * )malloc(sizeof(LinkNode));
    (*pHead)->next = NULL;
    (*pHead)->data = 0;
}

/**
    function : create a new LinkNode(as its name)
    parameter list : (1) data---the wished data in the new LinkNode
 */
LinkNode * createNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

/**
    function : traverse the linkedlist(as its name)
    parameter list : (1) pHead---the head pointer of the operated linkedlist
 */
void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;
    while (p != NULL) {
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
}

/**
    function : free the specific given linkedlist
    parameter list : pHead---the head pointer of the operater linkedlist
 */
void freeList(LinkNode * pHead) {
    if (pHead == NULL) return;

    LinkNode * p = pHead;
    LinkNode * temp;
    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}


//实现“删除链表中特定值的结点”算法的核心方法
int deleteByValue(LinkList pHead, int e) {
    int count = 0;          //count变量用于记录被删除的结点的个数
    LinkNode * q = NULL;    //临时指针变量q，q要指向被删除的结点
    LinkNode * p = pHead;   //临时指针变量p，初始化为头指针

    while(p->next != NULL) {    //只要链表中还有未遍历的元素，就一直遍历下去
        q = p->next;
        int data = q->data;

        if (data == e) {
            p->next = q->next;
            free(q);
            count++;
        } else {
            p = p->next;
        }
    }

    return count;
}
    LinkNode * p = pHead;   //临时指针变量p，初始化为头指针

    while(p->next != NULL) {    //只要链表中还有未遍历的元素，就一直遍历下去
        q = p->next;            //每次循环开始，都将q(当前要判断的结点)进行更新。
        int data = q->data;

        if (data == e) {
            p->next = q->next;
            free(q);
            count++;
        } else {
            p = p->next;
        }
    }

    return count;
}

                运行结果 : 

        3.算法的时间和空间复杂度：

        (1) 时间复杂度：
        main函数中的语句顺序执行，调用的核心方法deleteByValue中也就是遍历了一下链表，而遍历链表的时间复杂度是O(n)，所以根据时间复杂度计算的加法原则T(n) = T1(n) + T2(n) = O(f(n)) + O(g(n)) = O(max{f(n), g(n)})，总的时间复杂度 = O(1) + O(n) = O(n)。

        (2) 空间复杂度：

        只使用了几个额外的指针变量（p 和 q），这些都是常量级的空间，所以空间复杂度为O(1)。

---

二、链表链表最小值结点的删除

        0.题目 : 

        现有一带有头结点的单链表L，要求删除掉该链表的一个最小值结点（假设最小值结点是唯一的）。请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        显然我们要完成两个主要的操作——①找到这个最小的结点；②删除掉这个结点；

        如何找到最小的结点？

        需要遍历整个链表，所以首先得有一个temp指针来负责遍历链表，还需要有一个min指针来记录当前的最小的结点，就是说如果在遍历过程中发现temp指向的结点比min指向的结点还要小，就要更改min指针的指向，使其指向temp所指向的结点，然后temp指针继续参与链表的遍历，直至整个链表遍历完毕。所以“找”这个操作需要两个指针。

        如何删掉找到的结点？

        由于是非循环单链表，所以如果我们要删除一个结点，肯定就需要得到该结点的前驱结点，但是怎么得到前驱结点呢？指针！所以，对应于找操作的temp指针和min指针，“删”操作便有了对应的tempPre和minPre指针，见名知意，这两个指针分别指向temp的前驱结点和min的前驱结点。所以这个核心算法的实现一共需要四个指针。有同学可能有疑问？—— 如果要删除min指针指向的结点，那么肯定需要minPre来指向min的前驱结点，但是为什么还需要tempPre指针呢？因为随着链表的遍历，min指针是可能改变的，所以需要tempPre指针来帮忙，这样我们只需要minPre = tempPre就可以更新min指针了！

        2.C语言描述 : 

                完整代码如下：(注意看注释)

# include <stdio.h>
# include <stdlib.h>

//定义数据结构
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//函数声明
void initialize(LinkList * pHead);
LinkNode * createNode(int data);
void freeList(LinkNode * pHead);
void traverse(LinkList pHead);
void deleteMinimum(LinkList pHead);

int main(void) {
    LinkList pHead = NULL;              
    initialize(&pHead);                 //利用二级指针，初始化头指针，使其指向头结点。

    //给出一个具体的链表，用于测试该算法
    LinkNode * a1 = createNode(11);
    LinkNode * a2 = createNode(14);
    LinkNode * a3 = createNode(141);
    LinkNode * a4 = createNode(5);
    LinkNode * a5 = createNode(100);

    pHead->next = a1;                  
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;
    a5->next = NULL;

    printf("删除最小值前，链表情况如下——\n");
    traverse(pHead);
    
    deleteMinimum(pHead);
    printf("删除最小值后，链表情况如下——\n");
    traverse(pHead);
    freeList(pHead);

    return 0;
}

/**
    function : initialize(as its name)
    parameter list : (1) pHead---the pointer of the head pointer of the operated linkedlist
 */
void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode * ) malloc(sizeof(LinkNode));
    (*pHead)->next = NULL;
    (*pHead)->data = 0;
}

/**
    function : create a new LinkNode(as its name)
    parameter list : (1) data---the wished data in the new LinkNode
 */
LinkNode * createNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

/**
    function : traverse the linkedlist(as its name)
    parameter list : (1) pHead---the head pointer of the operated linkedlist
 */
void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;
    while (p != NULL) {
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
}

/**
    function : free the specific given linkedlist
    parameter list : pHead---the head pointer of the operater linkedlist
 */
void freeList(LinkNode * pHead) {
    if (pHead == NULL) return;

    LinkNode * p = pHead;
    LinkNode * temp;
    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

/**
    function : delete the minimum element of a linkedlist
    parameter list : (1) pHead---the head pointer of the operated linkedlist
 */
void deleteMinimum(LinkList pHead) {
    if (pHead == NULL || pHead->next == NULL) {
        printf("Please get one valid linkedlist~\n");
        return;
    }

    /*
        temp指针负责遍历链表，tempPre见名知意总是指向temp的前驱。
        min指针指向当前记录的最小的元素，minPre指针见名知意总是指向最小元素的前驱。
    */
    //tempPre指针和minPre指针初始化为头结点;
    //temp指针和min指针初始化为首结点;
    LinkNode * tempPre = pHead, * minPre = pHead;
    LinkNode * temp = pHead->next, * min = pHead->next;

    while (temp != NULL) {              //注意此处while循环的判断条件应该是temp不为NULL，因为temp此时表示首结点。
        if (temp->data < min->data) {   //如果当前遍历中指向的元素比已经记录的最小元素还小，就改变min指针。
            min = temp;
            minPre = tempPre;
        }                     
        tempPre = temp;                 //注意由于temp指针负责遍历链表，所以每一次循环它们的指向都要改变。
        temp = temp->next;
    }

    minPre->next = min->next;
    free(min);
}

                运行结果 : 

        3.算法的时间和空间复杂度 : 

        (1) 时间复杂度 : 
        实现算法的核心方法deleteMinimum只遍历了一次链表，所以时间复杂度是O(n)。

        (2) 空间复杂度 : 

        只使用了几个临时的辅助变量，所以算法的空间复杂度是O(1)，即算法是“原地工作”的。

---

三、链表的头插法

        0.题目 : 

        头插法建立带有头结点的单链表。请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        创建新结点后，先令新结点指向当前的首结点，再令头结点指向新结点。(头插法build的链表元素的值与输入的值顺序相反).

        2.C语言描述 : 

                完整代码如下：(注意看注释)

# include <stdio.h>
# include <stdlib.h>

//定义数据结构
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//函数声明
void initialize(LinkList * pHead);
LinkList headInsertion(LinkList pHead);
void freeList(LinkList pHead);
void traverse(LinkList pHeaed);

int main(void) {
    LinkList pHead = NULL;
    initialize(&pHead);

    //头插法建立单链表(从首结点开始建立)
    pHead = headInsertion(pHead);
    traverse(pHead);
    freeList(pHead);

    return 0;
}

/*
    function : initialize the HEAD NODE
*/
void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode * ) malloc(sizeof(LinkNode));
    (*pHead)->data = 0;
    (*pHead)->next = NULL;
}

LinkList headInsertion(LinkList pHead) {

    printf("请输入结点的值(输入-1表示结束链表的建立~)\n");
    int data;

    
    do {
        scanf("%d", &data);
        if (data == -1) break;

        LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
        p->data = data;

        p->next = pHead->next;      //新结点指向首结点
        pHead->next = p;            //头结点指向新结点  （最后达到的效果：头结点-->新的首结点-->旧的首结点）
    } while (data != -1);

    return pHead;
}

void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;

    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }

    printf("\n");
}

void freeList(LinkList pHead) {
    if (pHead == NULL) return;

    LinkNode * p = pHead;
    LinkNode * temp;

    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

                运行效果 : (如下GIF图)

        3.算法的时间和空间复杂度 : 

        (1) 时间复杂度 ：

        Time complexity: O(n), where n is the number of nodes inserted。Each insertion operation is O(1), but it's performed n times。

        (2) 空间复杂度 : 

        Space complexity: O(n), We create n new nodes, each taking constant space

---

四、链表的尾插法

        0.题目 : 

        尾插法建立带有头结点的单链表。请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        创建新结点后，直接让链表最后一个结点指向新结点。(尾插法build的链表元素的值与输入的值顺序一致).

        PS : 注意与头插法不同，尾插法由于是在头结点后面插入新元素，所以每次插入一个新的结点前，都需要把新结点的next指针置空。而如果是头插法，由于已经通过initialize函数初始化了头结点，所以头插法中不需要这一步操作。

        2.C语言描述 : 

                完整代码如下：(注意看注释)

#include <stdio.h>
#include <stdlib.h>

//定义数据结构 
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//函数声明
void initialize(LinkList * pHead);
LinkList tailInsertion(LinkList pHead);
void traverse(LinkList pHead);
void freeList(LinkList pHead);

int main(void) {
    LinkList pHead = NULL;
    initialize(&pHead);

    pHead = tailInsertion(pHead);
    traverse(pHead);
    freeList(pHead);

    return 0;
}

/*
    function : initialize(as its name);
    parameter list : (1) pHead---the head pointer of the operated linkedlist
*/
void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode * ) malloc(sizeof(LinkNode));
    (*pHead)->data = 0;
    (*pHead)->next = NULL;
}

/*
    function : CORE FUNCTION(built on prepared head node)
*/
LinkList tailInsertion(LinkList pHead) {
    printf("请输入结点的值(输入-1表示停止建立单链表~)\n");
    int data;
    LinkNode * rear = pHead;            //建立尾指针，初始化为头指针.

    do {
        scanf("%d", &data);
        if (data == -1) break;

        LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
        p->data = data;                 //修改新结点的值
        p->next = NULL;                 //What's most signifcant!!!!~

        rear->next = p;                 //让当前链表最后一个结点指向新结点(一开始是头结点指向首结点)
        rear = p;                       //更改rear的指向，使其指向链表的最后一个结点
    } while (data != -1);

    return pHead;                       //Don't forget your return value.
}

void traverse(LinkList pHead) {
    if (pHead == NULL || pHead->next == NULL) return;

    LinkNode * p = pHead->next;

    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }

    printf("\n");
}

void freeList(LinkList pHead) {
    if (pHead == NULL) return;

    LinkNode * p = pHead;
    LinkNode * temp;

    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

                运行效果 : (如下GIF图)

        3.算法的时间和空间复杂度 : 

        (1) 时间复杂度 : 

        Time Complexity: O(n), where n is the number of elements inserted, The loop runs n times, once for each input element.
        (2) 空间复杂度 : 

        Space Complexity: O(n), where n is the number of elements in the list. We allocate memory for each node in the list, so the space used grows linearly with the number of elements

---

五、链表的逆置

        0.题目 : 

        现有一个带有头结点的单链表，要求将该单链表进行逆置（头结点位置不变，其他携带有数据的结点会进行逆置）。请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        一般对带头结点的单链表进行逆置时，由于头结点不携带数据，所以它不会参与链表的逆置。也就是说，每完成一次逆置操作，头结点都会指向新的首结点，直到最后逆置完成。

        (1) 使用p指针指向刚开始的首结点（逆置完成后它会成为最后一个结点）

        (2) pNext指针指向p指向的结点的后一个结点，pNext指针指向的结点会不断的插入到当前的首结点之前（就是头插法的原理），所以每次完成一次“逆置”操作后，都需要把pNext指针重新更新为p指向的结点的后一个结点。

        (3) p指向的结点会随着逆置的进行不断后移，由于p指针始终指向这个结点，所以p指针会自动地跟着后移我们不用管。

        (4) 通俗点说，就是p指向的结点一开始是首结点，我们要源源不断地把这个结点后面的结点一个一个往前插，还必须得插到当前的首结点之前，看不懂代码可以自己试着在纸上画一下，秒懂。

        2.C语言描述 : 

                完整代码如下：(注意看注释)

#include <stdio.h>
#include <stdlib.h>

//定义数据结构
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//函数声明
void initialize(LinkList * pHead);
LinkNode * createNode(int data);
void traverse(LinkList pHead);
void freeList(LinkList pHead);
void reverseLinkedList(LinkList pHead);         //CORE FUNCTION

int main(void) {
    LinkList pHead = NULL;
    initialize(&pHead);

    //给出一个具体的链表，用于测试该算法
    LinkNode * a1 = createNode(11);
    LinkNode * a2 = createNode(10);
    LinkNode * a3 = createNode(9);
    LinkNode * a4 = createNode(8);
    LinkNode * a5 = createNode(7);
    LinkNode * a6 = createNode(6);
    LinkNode * a7 = createNode(5);

    pHead->next = a1;
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;
    a5->next = a6;
    a6->next = a7;
    a7->next = NULL;

    printf("逆置该链表前，链表情况如下———\n");
    traverse(pHead);
    reverseLinkedList(pHead);
    printf("逆置该链表后，链表情况如下———\n");
    traverse(pHead);

    freeList(pHead);

    return 0;
}

void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode * ) malloc(sizeof(LinkNode));
    (*pHead)->data = 0;
    (*pHead)->next = NULL;
}

LinkNode * createNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;
    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

void freeList(LinkList pHead) {
    LinkNode * p = pHead;
    LinkNode * temp;
    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

/*
    Original : pHead--->p--->pNext--->...
    Final : pHead--->pNext--->p--->...
*/
void reverseLinkedList(LinkList pHead) {
    LinkNode * p = pHead->next;
    LinkNode * pNext = p->next;         //要将pNext插入到p之前

    while (pNext != NULL) {
        p->next = pNext->next;          //先让p指向pNext之后的元素，防止链表断开（这时候pNext指向的结点被单独拎出来了）
        pNext->next = pHead->next;      //再让pNext指向的结点指向当前的首结点，也就是让pNext指向的结点从后面插到了前面(头插法)
        pHead->next = pNext;            //最后让头结点指向pNext（完成一次逆置过程）

        /*
            完成一次逆置后，p指向的结点已经被后移，相应的p指针也跟着后移了。
            但是pNext指向的结点被前移了，为了能够进行下一轮的逆置操作，还必须修改pNext的指针。
        */
        pNext = p->next;                    
    }
}

                运行结果 : 

        3.算法的时间和空间复杂度 : 

        (1) 时间复杂度 : 
        从p指针来看，我们只遍历了一次链表，所以时间复杂度为O(n)。
        (2) 空间复杂度 : 

        只使用了几个临时的辅助变量，所以空间复杂度为O(1)，即算法是原地工作的。

---

六、链表中特定区间元素的删除

        0.题目 : 

        给定一带有头结点的无序的单链表，要求删除值位于指定区间内（闭区间[a,b]）的所有结点。请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        直接循环遍历一下链表，用if条件语句判断是否满足删除条件即可。联系上文第一题“链表中特定值结点的删除”。

        2.C语言描述 : 

                完整代码如下：(注意看注释)

#include <stdio.h>
#include <stdlib.h>

//Data structure defining
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//Function declaration
void initialize(LinkList * pHead);
LinkNode * createNewNode(int data);
void traverse(LinkList pHead);
void freeList(LinkList pHead);
int deleteByRange(LinkList pHead, int a, int b);

int main(void) {
    LinkList pHead;
    initialize(&pHead);

    LinkNode * a1 = createNewNode(1);
    LinkNode * a2 = createNewNode(2);
    LinkNode * a3 = createNewNode(11);
    LinkNode * a4 = createNewNode(141);
    LinkNode * a5 = createNewNode(5);
    LinkNode * a6 = createNewNode(3);

    pHead->next = a1;
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;
    a5->next = a6;
    a6->next = NULL;

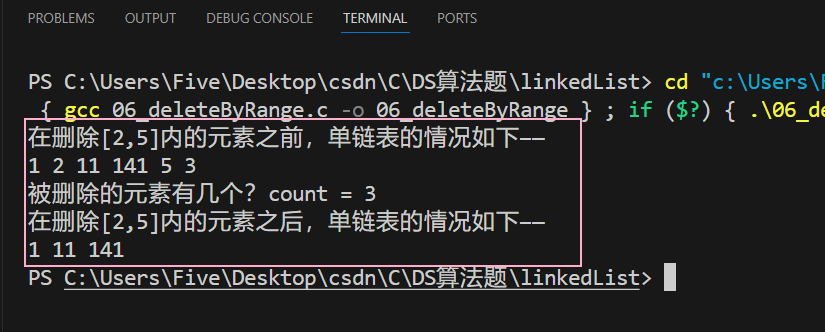
    printf("在删除[2,5]内的元素之前，单链表的情况如下——\n");
    traverse(pHead);

    int count = deleteByRange(pHead, 2, 5);
    printf("被删除的元素有几个？count = %d\n", count);

    printf("在删除[2,5]内的元素之后，单链表的情况如下——\n");
    traverse(pHead);
    freeList(pHead);

    return 0;
}

void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode * ) malloc(sizeof(LinkNode));
    (*pHead)->data = 0;
    (*pHead)->next = NULL;
}

LinkNode * createNewNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;

    while (p != NULL) {
        printf("%d ",p->data);
        p = p->next;
    }

    //better the effect of output
    printf("\n");
}

void freeList(LinkList pHead) {
    LinkNode * p = pHead;
    LinkNode * temp;

    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

int deleteByRange(LinkList pHead, int a, int b) {
    if (pHead == NULL || pHead->next == NULL) {
        return 0;
    }

    int count = 0;
    LinkNode * q = NULL;
    LinkNode * p = pHead;

    while (p->next != NULL) {
        q = p->next;
        int data = q->data;

        if (data >= a && data <= b) {
            p->next = q->next;
            free(q);
            count++;
        } else {
            p = p->next;
        }          
    }

    return count;
}

                运行结果 : 

        3.算法的时间和空间复杂度 : 

        (1) 时间复杂度 : 

        The algorithm traverses the list once, from the beginning to the end.

        For each node, it performs a constant-time operation (checking if the value is within the range and potentially deleting the node).

        In the worst case, it will visit every node in the list exactly once.

        Therefore, the time complexity is O(n), where n is the number of nodes in the linked list.

        (2) 空间复杂度 : 

        The algorithm uses a constant amount of extra space, regardless of the input size.

        It only uses two additional pointers (p and q) and an integer counter.

        No additional data structures are created that grow with the input size.

        Thus, the space complexity is O(1) or constant space.

---

七、找出两个链表的公共结点

        0.题目 : 

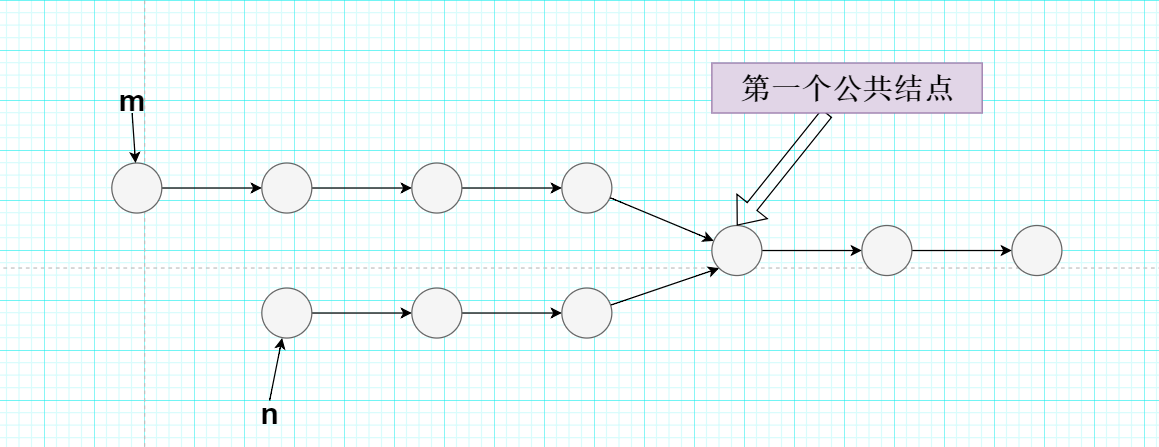
        已知有带头结点的单链表m和n，请判断它们是否有公共结点，并找出它们的第一个公共结点。（PS：公共结点指的是两个链表的前一个元素都指向了相同的后一个元素，如下图所示：）。

        请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        ①暴力解：用双指针分别遍历两个链表，先保持其中一个链表的指针不变，另一个链表的指针不断向后遍历，在此期间不停地判断两个指针的指向是否相同，如果在某一次循环过程中，发现用于遍历链表m和链表n的两个指针指向相同，说明当前指向的结点就是它们的公共结点，如果到遍历结束后都没有找到公共的结点，说明第一轮遍历没有收获，需要进行第二轮遍历，接着让之前保持不变的指针向后移动一位，另一个链表的指针重新开始不断向后遍历，以此类推，直到找到公共的结点，如果一直到前一个链表（其实就是外层链表）也遍历完毕还没找到公共结点，即整个循环结束后都没有找到公共结点，说明这两个链表其实不存在公共结点。

        ②优化解：设想如果链表m和链表n长度相同，即Length(m) == Length(n)，那么我们只需要让遍历两个链表的指针同步向后移动即可，直到链表表尾，如果在此期间发现了公共的结点，就返回，没有找到就说明这两个链表不存在公共结点。但是，更一般的情况是——两个链表是不等长的，这时候，我们只需要先得到两个链表的长度之差d，然后让较长的那个链表先向后遍历d个元素即可，这样又可以让遍历两个链表的指针来到同一起跑线上，并开始同步向后移动。

        那么，代码如何实现呢？ 

        ①暴力解代码思路——
        分别定义两个指针p和q，分别用于遍历链表m和链表n，然后双层for循环一套就完事儿了。别问我怎么写，自己去写一下就出来了。
        ②优化解代码思路——

        需要先定义一个函数getLength(LinkList pHead)，该函数见名知意用于获取指定链表的长度，通过这个函数我们可以知道两个链表的长度之差；然后判断这两个链表谁更长，把更长的那个链表先往后遍历”长度之差“个单位，然后p,q开始同步遍历找公共结点（该操作只需要一层while循环即可实现）。

        2.C语言描述 : 

                完整代码如下：(注意看注释)

#include <stdio.h>
#include <stdlib.h>

//Data structure defining
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//Function declaration
void initialize(LinkList * pHead);
LinkNode * createNewNode(int data);
int getLength(LinkList pHead);
void freeList(LinkList pHead);
LinkNode * findCommonNode(LinkList m,LinkList n);

int main(void) {
    LinkList m;
    LinkList n;
    initialize(&m);
    initialize(&n);

    //define nodes exclusive to m
    LinkNode * m1 = createNewNode(11);
    LinkNode * m2 = createNewNode(141);
    LinkNode * m3 = createNewNode(5);
    //define nodes exclusive to n
    LinkNode * n1 = createNewNode(666);

    //define some common nodes
    LinkNode * m4_n2 = createNewNode(521);
    LinkNode * m5_n3 = createNewNode(522);
    LinkNode * m6_n4 = createNewNode(523);

    //connect these nodes as we want
    m->next = m1;
    m1->next = m2;
    m2->next = m3;
    m3->next = m4_n2;
    m4_n2->next = m5_n3;
    m5_n3->next = m6_n4;
    m6_n4->next = NULL;

    n->next = n1;
    n1->next = m4_n2;
    // m4_n2->next = m5_n3;     //actually they're done just now
    // m5_n3->next = m6_n4;
    // m6_n4->next = NULL;

    LinkNode * firstCommonNode = findCommonNode(m, n);
    printf("\n\nThe value of the first common node is :%d\n\n", firstCommonNode->data);
    freeList(m);
    freeList(n);

    return 0;
}

void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode *) malloc(sizeof(LinkNode));
    (*pHead)->data = 0;
    (*pHead)->next = NULL;
}

LinkNode * createNewNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

int getLength(LinkList pHead) {
    LinkNode * p = pHead->next;
    int length = 0;

    while (p != NULL) {
        length++;
        p = p->next;
    }

    return length;
}

void freeList(LinkList pHead) {
    LinkNode * p = pHead;
    LinkNode * temp;

    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

LinkNode * findCommonNode(LinkList m, LinkList n) {

    
    LinkNode * p = m->next;         //p is origianlly initialized to the head node of m
    LinkNode * q = n->next;         //q is origianlly initialized to the head node of n

    /*-----------------------------------------------------------------------
        Brute force solution---Code Following
        -----------------------------------------------------------------------
        
    while (p != NULL) {
        while (q != NULL) {
            if (q == p) {
                return q;
            } else {
                q = q->next;
            }
        }

        p = p->next;                //after every end of the external loop, update the p and q
        q = n->next;
    }

    return NULL;                    //return NULL if there is no common node found
    */


/*-----------------------------------------------------------------------
    optimized solution---FOLLOWING
-----------------------------------------------------------------------*/
    
    int length_M = getLength(m);
    int length_N = getLength(n);
    int variancne = (length_M >= length_N) ? (length_M - length_N) : (length_N - length_M);

    /*
        let the pointer p always point to the longer list,
        which can reduce the code(REDUCE CODE DUPLICATION)
    */

    if (length_M < length_N) {
        LinkNode * temp = p;        
        p = q;
        q = temp;
    }

    for (int i = 0; i < variancne; ++i) {
        p = p->next;            //firstly aligned the p pointer and the q pointer.
    }

    while (q != NULL) {
        if (q == p) {
            return q;
        } else {
            p = p->next;
            q = q->next;
        }
    }

    return NULL;
    
}

        3.算法的时间和空间复杂度 : 

        (1) 暴力解法 : 
        ①时间复杂度——O(m * n)
        ②空间复杂度——O(1)
        (2) 优化解法 : 

        ①时间复杂度——O(m + n)
        ②空间复杂度——O(1)

---

八、链表奇偶位序元素的分离

        0.题目 : 

        已知一个带有头结点的单链表A，现要求将其分解为两个带有头结点的单链表A和B，使得A表中含有原来表中序号为奇数的元素，而B表中含有原来表中序号为偶数的元素，且保持其相对顺序不变。PS : 位序从1开始，即首结点的位序是1，第二个结点的位序是2，以此类推。

        请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        循环遍历链表A，可以借助一个int类型变量i来记录当前结点的位序（位序从1开始），如果i对2取余等于1，说明当前结点的位序是奇数，需要留在链表A中；如果i对2取余等于0，说明当前结点的位序是偶数，需要被插入到链表B中；最后循环结束，返回B。

        插入过程就是“尾插法”的实现，尾插法我们上面第五题已经说过了，这里就不废话了，大家直接看代码就就行，看不懂的纸上画俩链表模拟一下，立马就会了。

        2.C语言描述 : 

                完整代码如下：(注意看注释)

#include <stdio.h>
#include <stdlib.h>

//Data structure defining
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//Function declaration
void initialize(LinkList * pHead);
LinkNode * createNewNode(int data);
void traverse(LinkList pHead);
void freeList(LinkList pHead);
LinkList separateOddAndEvenByNumber(LinkList A);

int main(void) {
    LinkList A;
    initialize(&A);

    LinkNode * a1 = createNewNode(1);
    LinkNode * a2 = createNewNode(2);
    LinkNode * a3 = createNewNode(11);
    LinkNode * a4 = createNewNode(141);
    LinkNode * a5 = createNewNode(5);
    LinkNode * a6 = createNewNode(3);

    A->next = a1;
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;
    a5->next = a6;
    a6->next = NULL;

    printf("The A's condition before separating: ");
    traverse(A);

    LinkList B = separateOddAndEvenByNumber(A);

    printf("The A's condition after separating: ");
    traverse(A);
    printf("The B's condition: ");
    traverse(B);

    freeList(A);
    freeList(B);

    return 0;
}

void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode *) malloc(sizeof(LinkNode));
    (*pHead)->data = 0;
    (*pHead)->next = NULL;
}

LinkNode * createNewNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;

    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }

    printf("\n");
}

void freeList(LinkList pHead) {
    LinkNode * p = pHead;
    LinkNode * temp;

    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

LinkList separateOddAndEvenByNumber(LinkList A) {
    LinkList B;
    initialize(&B);

    LinkNode * p = A->next;             //p is initialized to the head node of A
    LinkNode * q = A;                   //q point to the previous node of p
    LinkNode * rearB = B;               //rearB point to the end node of B
    int i = 1;
    while (p != NULL) {
        if (i % 2 == 1) {               //Odd
            q = q->next;
            p = p->next;
        } else if (i % 2 == 0) {        //Even (need tail-insersion)
            rearB->next = p;
            rearB = p;
            q->next = p->next;
            p = q->next;
        }
        ++i;
    }
    rearB->next = NULL;

    return B;
}

                运行结果 : 

        3.算法的时间和空间复杂度 : 

        (1) 时间复杂度 : 
        The time complexity of your algorithm is O(n), where n is the number of nodes in the input linked list.
        (2) 空间复杂度：

        The space complexity of your algorithm is O(1), which means it uses constant extra space.

---

九、链表奇偶位序元素的分离但一个头插一个尾插

        0.题目 : 

        已知一个带有头结点的单链表list = {a1, b1, a2, b2, ..., an, bn}，现要求将其拆分为两个线性表listA和listB，使得listA = {a1, a2, ..., an}, listB = {bn, bn-1, ..., b2, b1}。请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        可知此题与第八题有些相似，因为要分离的元素恰好也是按奇偶位序来分离的，只不过此题要求我们将分离出去的元素分别存放在两个新的子链表中，并且，listA链表中的元素相对顺序保持不变，而listB链表中的元素相对顺序实现了倒置。

        不难想到，我们可以借鉴上一题(第八题) 的思路，并利用头插法和尾插法分别得到listB和listA。（头插法使得构造的listB链表的元素是倒置的。）

        PS : 这个题最好要与上面第八题一起记忆和学习。

        2.C语言描述 : 

                完整代码如下：(注意看注释)

#include <stdio.h>
#include <stdlib.h>

//Data Structure Defining
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//Functions Declaration
void initialize(LinkList * pHead);
LinkNode * createNewNode(int data);
void traverse(LinkList pHead);
void freeList(LinkList pHead);
void byHeadAndTailInsersion(LinkList pHead, LinkList * listA, LinkList * listB);

int main(void) {
    LinkList pHead;
    initialize(&pHead);

    LinkList listA,listB;
    initialize(&listA);
    initialize(&listB);

    LinkNode * a1 = createNewNode(1);
    LinkNode * a2 = createNewNode(2);
    LinkNode * a3 = createNewNode(3);
    LinkNode * a4 = createNewNode(4);
    LinkNode * a5 = createNewNode(5);
    LinkNode * a6 = createNewNode(6);

    pHead->next = a1;
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;
    a5->next = a6;
    a6->next = NULL;

    printf("The ORIGINAL list before separating: ");
    traverse(pHead);

    //巧妙利用二级指针，避免返回值问题。
    byHeadAndTailInsersion(pHead, &listA, &listB);

    printf("The listA's condition after separating: ");
    traverse(listA);
    printf("The listB's condition after separating: ");
    traverse(listB);

    freeList(pHead);
    freeList(listA);
    freeList(listB);

    return 0;
}

void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode *) malloc(sizeof(LinkNode));
    (*pHead)->data = 0;
    (*pHead)->next = NULL;
}

LinkNode * createNewNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;

    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }

    printf("\n");
}

void freeList(LinkList pHead) {
    LinkNode * p = pHead;
    LinkNode * temp;

    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

void byHeadAndTailInsersion(LinkList pHead, LinkList * listA, LinkList * listB) {
    LinkNode * p = pHead->next;
    LinkNode * rearA = (*listA); //Because listA will use tail insersion, so this move make it easier.

    int i = 1;                  //To record current node's number(start from 1)
    
    while (p != NULL) {
        //Create a new node to avoid modifying the original list structure, To avert the disconnection in the process of tail-insersion
        LinkNode* newNode = createNewNode(p->data);
        /*
            If current node is with an odd-number, then insert it into the listA by tail Insersion.
        */
        if (i % 2 == 1) {
            rearA->next = newNode;
            rearA = newNode;
        } else if (i % 2 == 0) {
            /*
                Else, if current node is with an even-number,
                then insert it into the listB with head insersion.
            */
            newNode->next = (*listB)->next;
            (*listB)->next = newNode;
        }
        ++i;                    //Don't forget this one.
        p = p->next;
    }
}

                运行结果 ：

        3.算法的时间和空间复杂度 : 

        (1) 时间复杂度 ：

        The time complexity of your algorithm is O(n), where n is the number of nodes in the input linked list.

• The algorithm traverses the entire input list once.
• For each node, it performs constant time operations (creating a new node and inserting it into either listA or listB).
• The while loop runs n times, where n is the number of nodes in the original list.
• All operations inside the loop (creating new node, comparisons, pointer assignments) are O(1).

        Therefore, the overall time complexity is O(n).

        (2) 空间复杂度：

        The space complexity of your algorithm is O(n), where n is the number of nodes in the input linked list.

• The algorithm creates a new node for each element in the original list.
• ListA and ListB together will contain exactly n new nodes (where n is the number of nodes in the original list).
• The space used grows linearly with the input size.
• No additional data structures are used that grow with the input size beyond the new nodes created.

        Therefore, the space complexity is O(n).

---

十、链表的去重

        0.题目 : 

        在一个递增且有序的线性表中，已知存在数值相同的元素存在，若该线性表以单链表方式存储，请设法去掉链表中数值相同的结点，使得表中不再有重复的元素。请设计一个算法来实现上述操作，用C语言描述该算法，并且计算出该算法的时间复杂度和空间复杂度。

        1.算法设计思想 : 

        由于单链表是递增有序的，所以若存在值重复的结点，那么这些结点一定是排列在一块儿的。所以，我们只需要在遍历链表的时候使用两个指针，一前一后，判断它们指向的结点的值是否相同，如果相同，就进行链表结点的删除，否则就仅移动指针。

        注意要与“顺序表”的去重进行对比，顺序表去重的关键点是要让去重后剩余的元素仍然是一个连续的顺序表，也就是涉及到元素移动的问题，当时我们是借助一个count变量来解决的。

        2.C语言描述 : 

                完整代码如下：(注意看注释)

#include <stdio.h>
#include <stdlib.h>

//Data Structure Defining
typedef struct LinkNode {
    int data;
    struct LinkNode * next;
} LinkNode, * LinkList;

//Functions Declaration
void initialize(LinkList * pHead);
LinkNode * createNewNode(int data);
void traverse(LinkList pHead);
void freeList(LinkList pHead);
int removeDuplicate(LinkList pHead);

int main(void) {
    LinkList pHead;
    initialize(&pHead);

    LinkNode * a1 = createNewNode(1);
    LinkNode * a2 = createNewNode(2);
    LinkNode * a3 = createNewNode(2);
    LinkNode * a4 = createNewNode(3);
    LinkNode * a5 = createNewNode(3);
    LinkNode * a6 = createNewNode(4);

    pHead->next = a1;
    a1->next = a2;
    a2->next = a3;
    a3->next = a4;
    a4->next = a5;
    a5->next = a6;
    a6->next = NULL;

    printf("\nThe ORIGINAL list before removing duplicates: ");
    traverse(pHead);

    int count = removeDuplicate(pHead);
    printf("去重操作一共删除了几个结点？%d个",count);

    printf("\nThe FINAL list after removing duplicates: ");
    traverse(pHead);

    freeList(pHead);

    return 0;
}

void initialize(LinkList * pHead) {
    (*pHead) = (LinkNode * ) malloc(sizeof(LinkNode));
    (*pHead)->data = 0;
    (*pHead)->next = NULL;
}

LinkNode * createNewNode(int data) {
    LinkNode * p = (LinkNode * ) malloc(sizeof(LinkNode));
    p->data = data;
    p->next = NULL;

    return p;
}

void traverse(LinkList pHead) {
    LinkNode * p = pHead->next;

    while (p != NULL) {
        printf("%d ", p->data);
        p = p->next;
    }

    printf("\n");
}

void freeList(LinkList pHead) {
    LinkNode * p = pHead;
    LinkNode * temp;
    
    while (p != NULL) {
        temp = p;
        p = p->next;
        free(temp);
    }
}

/**
    pointer prev will point to the previous node of current node, and it's initialized with the head node.
    pointer current, as its name, just point to the current node.
 */
int removeDuplicate(LinkList pHead) {
    LinkNode * prev = pHead;
    LinkNode * current = prev->next;
    LinkNode * temp;
    int count = 0;              //To record the number of deleted nodes.

    if (current->next == NULL || current == NULL) {
        return 0;
    }

    while (current != NULL && current->next != NULL) {
        if (current->data == current->next->data) {
            temp = current;
            prev->next = current->next;
            free(temp);
            count++;
            current = prev->next;
        } else {
            prev = prev->next;
            current = current->next;
        }
    } 

    return count;
}

                运行结果 : 

        3.算法的时间和空间复杂度 : 

        (1) 时间复杂度：
        一次遍历就完成了去重，时间复杂度为O(n)。

        (2) 空间复杂度：
        只使用了几个临时的辅助变量，所以空间复杂度为O(1)。

---

Δ总结

• 又写到两万多字了，文章编辑器一卡一卡的，老规矩，人不能被尿憋死！剩余的链表相关的算法题up会重新开一篇博文，到时候会将链接放在下面（才不是因为又可以水一篇博文呢！）。
• 这篇博文一共只有十道题，综合来看一道难题没有，全部是easy-level的算法题，在链表算法的下篇中，up会引入几道408算法真题，大家不见不散。
• 🆗，以上就是这篇博文的全部内容了，感谢阅读！

        System.out.println("END-------------------------------------------");