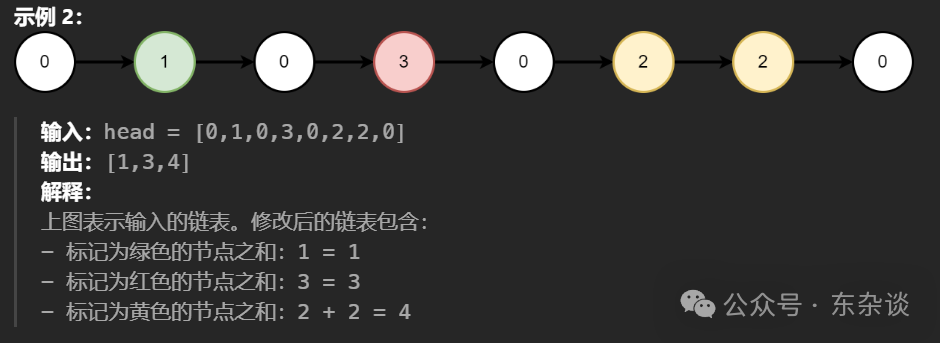
全排列：

原理：

经典回溯。回溯的原理：用一个数组来记录路径，每次递归，都访问没访问到的元素（怎么访问：当然是遍历），访问完弹出上一步。

解：

同原理，在路径访问后，判断该路径是否符合条件即可。

子集：

原理：

经典回溯

解：

没啥说的，符合条件的path加进去就好了

电话号码的字母组合：

原理：

相当于把排列组合的原始数组变成了电话号上的字母，只需要取出数字对应的字母，然后把字母排列组合就好。

解：

同原理。

组合总和：

原理：

写出所有排列组合，判断是否符合条件即可。但可以剪枝，比如target-当前值<0的。

解：

同原理。

括号生成：

原理：

其实也是枚举所有排列组合。但需要剪枝，左括号平衡（数量相等），所以可以传递左右括号的数量，然后判断加左还是加右。

解：

加完左括号弹出左括号加右括号，这种，然后加剪枝判断是否需要加左右括号即可。

单词搜索：

原理：

对四个方向进行递归查找（很像岛屿的数量这道题，但是这个是需要回溯把走过的路径记录、比较、回溯抹除路径）。

解：

同原理。

分割回文串：

原理：

一眼盯真，鉴定为纯纯的得到所有“，”的排列组合，然后判断是不是回文。但是这个只是最初版本，也就是说，遍历所有可能分割，然后判断是不是回文。

解：

遍历谁都会，但需要剪枝，我们在递归前判断是否是回文，就减少了一次递归（所以非剪枝版本就是在for循环外面去判断是否是回文）。策略是：每次从起点left一个一个、依次判断分割后是不是回文。如果是，就可以继续分割。不是就不分割。

N皇后：

原理：

我们从分割回文串，了解到，在for循环内进行判断，就是剪枝。所以，依旧用分割回文串的思想。每次递归遍历一行，给这一行的不同位置放上皇后，判断是否成立。成立的条件，就是列、和对角线上没有其他皇后。

解：

同原理。

搜索插入位置：

原理：

没得说，二分查找。

解：

同原理。

搜索二维矩阵：

原理：

没啥说的，二分秒了。

在排序数组中查找元素的第一个和最后一个位置：

原理：

普通二分改进版，在mid==target的时候，检查前面\后面是否也有target，有的话就收缩，没有就返回。

解：

同原理。

【忍者算法】LeetCode 34 在排序数组中查找元素的第一个和最后一个位置_哔哩哔哩_bilibili

搜索旋转排序数组：

原理：

只判断有序的一边，如果没在有序的一边，就在另一边。怎么判断有序：中点比最左大，左边就有序，中点比左边小左边就无序。然后判断target在左还是在右

解：

同原理。

寻找旋转排序数组中的最小值：

原理：

搜索旋转排序数组那个，结果在有序的里，而这个，结果则是在无序的里，所以往上一题相反的方向二分，即可得到结果。

寻找两个正数数组的中位数：

原理：

4. 寻找两个正序数组的中位数 Median of Two Sorted Arrays 【LeetCode 力扣官方题解】_哔哩哔哩_bilibili

这个不懂？？有点难

有效括号：

原理:

栈的经典题目，左括号压栈，右括号出栈对比。

最小栈：

原理：

两个栈实现，这个第一次做可能有点儿懵，就是一个栈存当前最小值，一个栈存当前值。弹就一起弹，压就压当前值和栈顶的最小值。

字符串解码：

原理：

由内而外展开的过程。对应了栈的先进后出。说白了就是栈去解递归（模拟递归）保存当前状态，进入下一状态。

解：

解决展开问题，遇到左括号说明内部需要展开，记录展开的起点和次数。遇到右括号说明内部展开完了，只要从记录的起点展开（复制）展开次数，就可以得出结果。

每日温度：

原理：

单调栈，[数据结构]——单调栈-CSDN博客，

作用：找第一个比ta大的元素。

解：

单调栈，当前元素小于栈顶就入栈，大于栈顶就把比它小的出栈，并给小的赋值。

柱状图中最大的矩形：

原理：

还是单调栈，单调递增栈，递增栈的每种组合：如图：

当遍历到2，需要弹出5,6时计算红色和黄色的面积（当前弹出块的高度*到2的距离）。

还要注意：在最后可能栈里还剩下几个元素，特殊处理依次弹出计算面积即可（注意最后一个，即最小元素，会横向铺满整个的，如1，蓝色框框）

解：

同原理，细节蛮多的，未来再说，先把思路打通

数组中第k个最大元素：

原理：

可以用堆秒了，但是如果想更快，就要用快排思想进行折半。

解：

没啥，先用大顶堆秒了。

前k个高频元素：

原理：

依旧是大顶堆，先算出现次数，然后根据出现次数堆排即可。

数据流的中位数：

LeetCode 295｜数据流的中位数｜大顶堆｜小顶堆｜经典困难题_哔哩哔哩_bilibili

原理：

虽然上面比我说的清楚，但是原理大概就是，两个堆，一个大顶堆，维护前半部分的数；一个小顶堆，维护后半部分的数。加入新的数时，大的放小顶堆，小的放大顶堆，如果放入小顶堆，那么小顶堆弹出堆顶元素插入大顶堆。放入大顶堆反之，以大小顶堆的堆顶元素，维护中位数。

买卖股票的最佳时机：

原理：

买卖股票的最佳时机【基础算法精讲 21】_哔哩哔哩_bilibili

把当前状态做一个状态机。然后根据状态机写递推公式即可。

解：

dp[i][0]:第i天未持有的状态：如果买入，-price,因为只买入一次，只需要记录最小的一次买入；什么都不做就等于dp[i-1][0];

dp[i][1]:第i天持有股票的状态：如果卖出，+price，需要记录上一步买入的花了多少，所以要加上dp[i-1][0]；什么都不做就等于dp[i-1][1];

跳跃游戏：

原理：

遍历，每次遍历到一个数，找出当前覆盖的最大范围。如果遍历的索引超出最大范围了，说明跳不到当前索引的位置。