参考文献 代码随想录
一、长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的
子数组
[numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4] 输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1] 输出:0
提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
进阶:
- 如果你已经实现
O(n)时间复杂度的解法, 请尝试设计一个O(n log(n))时间复杂度的解法。
暴力
class Solution(object): def minSubArrayLen(self, target, nums): """ :type target: int :type nums: List[int] :rtype: int """ # 暴力思路: 2层循环寻找和大于等于target的,然后并计算长度 # 定义一个临时变量result存放的是和大于等于target的最小长度 result = float('inf') for i in range(len(nums)): # 先从每一个元素开始找 tmpSum = 0 # 临时存放每个长度之和 for j in range(i, len(nums)): # 找这个元素后面的元素 tmpSum += nums[j] if tmpSum >= target: # 一旦找到,此时必定是当前最小的长度 result = min(result, j - i + 1) break # 调出循环 if result == float('inf'): return 0 return result
滑动窗口(双指针)
使用2个指针,一个慢指针(就是更新的值没有另外一个指针快),一个快指针(同理),还需要定义一个变量,接受对应长度的和,result变量统计最小长度之和大于等于target的,然后while循环,那么这个while循环的条件是什么呢?是快指针小于数组的长度,那为什么不判断慢指针呢?因为快指针比慢指针更快到达数组的长度,在while循环,统计和,然后判断此时的和是否大于等于target,问题来了?是使用if呢,还是while呢,这里举一个例子:假设target = 3,数组为[2,3,1,2,4,3],当统计到3,1,2,4的时候,此时是大于target的,那么当满足条件后,移动慢指针时,剩下的还是大于等于target,所以使用while判读,条件成立后,对应的长度=快-慢+1,然后先对和做减法,然后在移动,为什么?因为如果你先移动慢指针,那么在对和做减法的话,就会出错。
class Solution(object): def minSubArrayLen(self, target, nums): """ :type target: int :type nums: List[int] :rtype: int """ # 滑动窗口: 双指针寻找和大于等于target的,然后并计算长度, # 定义一个临时变量result存放的是和大于等于target的最小长度 result = float('inf') slow = 0 fast = 0 tmpSum = 0 # 记录临时对应长度的和 while fast < len(nums): tmpSum += nums[fast] while tmpSum >= target: # 为什么要使用while,因为当你移动慢指针的时候,结果还可能大于等于target result = min(result, fast - slow + 1) tmpSum -= nums[slow] # 把慢指针向后移,那么这个和就要减去 slow += 1 fast += 1 if result == float('inf'): return 0 return result
二、螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:

输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 20
思路
总体思路是创建一个 n x n 的矩阵并按螺旋顺序填充数字。步骤如下:(方向的控制,只有遇到超出边界的时候,才调整方向(难点:如何调整方向))
-
初始化:创建一个
n x n的矩阵,所有位置初始化为 0。定义四个方向(右、下、左、上)来控制填充顺序。 -
填充逻辑:
- 从矩阵的起始位置(通常是 (0, 0))开始填充数字。
- 根据当前方向(右、下、左、上)填充下一个位置的数字。
- 如果遇到矩阵边界或已填充的位置,改变方向。
- 重复这个过程,直到矩阵完全填充。
-
方向控制:使用方向数组和索引来控制填充方向。当无法继续沿当前方向填充时,更新方向索引以切换方向。
这种方法确保了螺旋填充的正确性,逐步向内完成整个矩阵。
class Solution(object): def generateMatrix(self, n): matrix = [[0] * n for _ in range(n)] directions = [(0, 1), (1, 0), (0, -1), (-1, 0)] # 右、下、左、上 x, y = 0, 0 direction_index = 0 for num in range(1, n * n + 1): # num代表的是螺旋矩阵的每个元素 matrix[x][y] = num next_x, next_y = x + directions[direction_index][0], y + directions[direction_index][1] # 向某个方向填充(右、下、左、上) if (0 <= next_x < n and 0 <= next_y < n and matrix[next_x][next_y] == 0): # 判断边界 x, y = next_x, next_y else: #如果超过边界,那么就要处理 direction_index = (direction_index + 1) % 4 # direction_index 控制方向 x += directions[direction_index][0] y += directions[direction_index][1] return matrix
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
由外向内一圈一圈这么画下去。
可以发现这里的边界条件非常多,在一个循环中,如此多的边界条件,如果不按照固定规则来遍历,那就是一进循环深似海,从此offer是路人。
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
那么我按照左闭右开的原则,来画一圈,大家看一下:

这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
这也是坚持了每条边左闭右开的原则。
一些同学做这道题目之所以一直写不好,代码越写越乱。
就是因为在画每一条边的时候,一会左开右闭,一会左闭右闭,一会又来左闭右开,岂能不乱。
代码如下,已经详细注释了每一步的目的,可以看出while循环里判断的情况是很多的,代码里处理的原则也是统一的左闭右开。
class Solution: def generateMatrix(self, n: int) -> List[List[int]]: nums = [[0] * n for _ in range(n)] startx, starty = 0, 0 # 起始点 loop, mid = n // 2, n // 2 # 迭代次数、n为奇数时,矩阵的中心点 count = 1 # 计数 for offset in range(1, loop + 1) : # 每循环一层偏移量加1,偏移量从1开始 for i in range(starty, n - offset) : # 从左至右,左闭右开,offset控制的是每次填充的边界 nums[startx][i] = count count += 1 # 向右填,那么对应的行不动 for i in range(startx, n - offset) : # 从上至下 nums[i][n - offset] = count # 向下填,那么列不动 count += 1 for i in range(n - offset, starty, -1) : # 从右至左 nums[n - offset][i] = count# 向左填,那么对应的行不动 count += 1 for i in range(n - offset, startx, -1) : # 从下至上 nums[i][starty] = count# 向上填,那么列不动 count += 1 startx += 1 # 更新起始点 starty += 1 if n % 2 != 0 : # n为奇数时,填充中心点 nums[mid][mid] = count return nums
三、区间和
题目描述
给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。
输入描述
第一行输入为整数数组 Array 的长度 n,接下来 n 行,每行一个整数,表示数组的元素。随后的输入为需要计算总和的区间下标:a,b (b > = a),直至文件结束。
输出描述
输出每个指定区间内元素的总和。
输入示例
5
1
2
3
4
5
0 1
1 3输出示例
3
9提示信息
数据范围:
0 < n <= 100000
问题分析
每个元素记录之前的和,然后利用对应的下标值相减即可
n = int(input()) li = [] for _ in range(n): if not li: li.append(int(input())) else: li.append(li[-1] + int(input())) target = [] try: while 1: a, b = map(int, input().split()) if a == 0: target.append(li[b]) else: target.append(li[b] - li[a - 1]) except: pass for i in target: print(i)
四、开发商购买土地
题目描述
在一个城市区域内,被划分成了n * m个连续的区块,每个区块都拥有不同的权值,代表着其土地价值。目前,有两家开发公司,A 公司和 B 公司,希望购买这个城市区域的土地。
现在,需要将这个城市区域的所有区块分配给 A 公司和 B 公司。
然而,由于城市规划的限制,只允许将区域按横向或纵向划分成两个子区域,而且每个子区域都必须包含一个或多个区块。 为了确保公平竞争,你需要找到一种分配方式,使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。
注意:区块不可再分。
输入描述
第一行输入两个正整数,代表 n 和 m。
接下来的 n 行,每行输出 m 个正整数。
输出描述
请输出一个整数,代表两个子区域内土地总价值之间的最小差距。
输入示例
3 3
1 2 3
2 1 3
1 2 3输出示例
0提示信息
如果将区域按照如下方式划分:
1 2 | 3
2 1 | 3
1 2 | 3
两个子区域内土地总价值之间的最小差距可以达到 0。
数据范围:
1 <= n, m <= 100;
n 和 m 不同时为 1。
问题分析
只能横向或者说是纵向切,那么我们就要算出,横向切,之后的最小值,纵向切,之后的最小,那么就可以了
def main(): import sys input = sys.stdin.read data = input().split() idx = 0 n = int(data[idx]) idx += 1 m = int(data[idx]) idx += 1 sum = 0 # 保存总的价值 vec = [] for i in range(n): row = [] for j in range(m): num = int(data[idx]) idx += 1 row.append(num) sum += num vec.append(row) # 统计横向 horizontal = [0] * n for i in range(n): for j in range(m): horizontal[i] += vec[i][j] # 统计纵向 vertical = [0] * m for j in range(m): for i in range(n): vertical[j] += vec[i][j] result = float('inf') horizontalCut = 0 for i in range(n): horizontalCut += horizontal[i] # 切割 # sum - 2 * horizontalCut 和 sum - horizontalCut - horizontalCut等价 result = min(result, abs(sum - 2 * horizontalCut)) verticalCut = 0 for j in range(m): verticalCut += vertical[j] result = min(result, abs(sum - 2 * verticalCut)) print(result) if __name__ == "__main__": main()
数组总结篇#
数组理论基础
数组是非常基础的数据结构,在面试中,考察数组的题目一般在思维上都不难,主要是考察对代码的掌控能力
也就是说,想法很简单,但实现起来 可能就不是那么回事了。
首先要知道数组在内存中的存储方式,这样才能真正理解数组相关的面试题
数组是存放在连续内存空间上的相同类型数据的集合。
数组可以方便的通过下标索引的方式获取到下标对应的数据。
举一个字符数组的例子,如图所示:
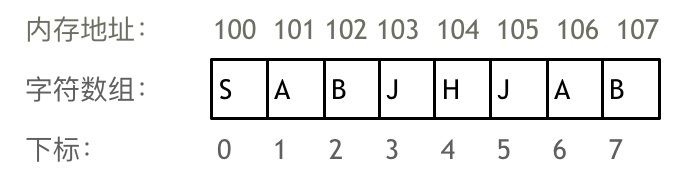
需要两点注意的是
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
正是因为数组在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。
例如删除下标为3的元素,需要对下标为3的元素后面的所有元素都要做移动操作,如图所示:
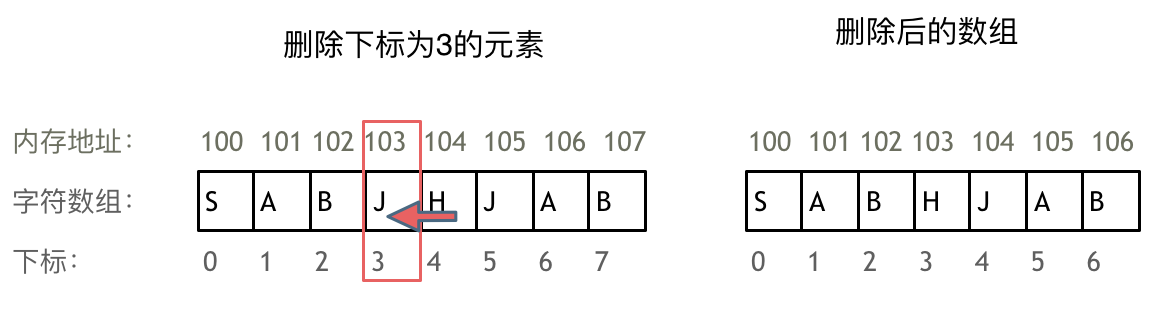
而且大家如果使用C++的话,要注意vector 和 array的区别,vector的底层实现是array,严格来讲vector是容器,不是数组。
数组的元素是不能删的,只能覆盖。
那么二维数组直接上图,大家应该就知道怎么回事了

那么二维数组在内存的空间地址是连续的么?
我们来举一个Java的例子,例如: int[][] rating = new int[3][4]; , 这个二维数组在内存空间可不是一个 3*4 的连续地址空间
看了下图,就应该明白了:

所以Java的二维数组在内存中不是 3*4 的连续地址空间,而是四条连续的地址空间组成!
#数组的经典题目
在面试中,数组是必考的基础数据结构。
其实数组的题目在思想上一般比较简单的,但是如果想高效,并不容易。
我们之前一共讲解了四道经典数组题目,每一道题目都代表一个类型,一种思想。
#二分法
数组:每次遇到二分法,都是一看就会,一写就废(opens new window)
这道题目呢,考察数组的基本操作,思路很简单,但是通过率在简单题里并不高,不要轻敌。
可以使用暴力解法,通过这道题目,如果追求更优的算法,建议试一试用二分法,来解决这道题目
- 暴力解法时间复杂度:O(n)
- 二分法时间复杂度:O(logn)
在这道题目中我们讲到了循环不变量原则,只有在循环中坚持对区间的定义,才能清楚的把握循环中的各种细节。
二分法是算法面试中的常考题,建议通过这道题目,锻炼自己手撕二分的能力。
#双指针法
- 数组:就移除个元素很难么?(opens new window)
双指针法(快慢指针法):通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
- 暴力解法时间复杂度:O(n^2)
- 双指针时间复杂度:O(n)
这道题目迷惑了不少同学,纠结于数组中的元素为什么不能删除,主要是因为以下两点:
- 数组在内存中是连续的地址空间,不能释放单一元素,如果要释放,就是全释放(程序运行结束,回收内存栈空间)。
- C++中vector和array的区别一定要弄清楚,vector的底层实现是array,封装后使用更友好。
双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。
#滑动窗口
- 数组:滑动窗口拯救了你(opens new window)
本题介绍了数组操作中的另一个重要思想:滑动窗口。
- 暴力解法时间复杂度:O(n^2)
- 滑动窗口时间复杂度:O(n)
本题中,主要要理解滑动窗口如何移动 窗口起始位置,达到动态更新窗口大小的,从而得出长度最小的符合条件的长度。
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。
如果没有接触过这一类的方法,很难想到类似的解题思路,滑动窗口方法还是很巧妙的。
#模拟行为
- 数组:这个循环可以转懵很多人!(opens new window)
模拟类的题目在数组中很常见,不涉及到什么算法,就是单纯的模拟,十分考察大家对代码的掌控能力。
在这道题目中,我们再一次介绍到了循环不变量原则,其实这也是写程序中的重要原则。
相信大家有遇到过这种情况: 感觉题目的边界调节超多,一波接着一波的判断,找边界,拆了东墙补西墙,好不容易运行通过了,代码写的十分冗余,毫无章法,其实真正解决题目的代码都是简洁的,或者有原则性的,大家可以在这道题目中体会到这一点。
#前缀和
代码随想录后续补充题目
- 数组:求取区间和(opens new window)
前缀和的思路其实很简单,但非常实用,如果没接触过的录友,也很难想到这个解法维度,所以 这是开阔思路 而难度又不高的好题。
#总结
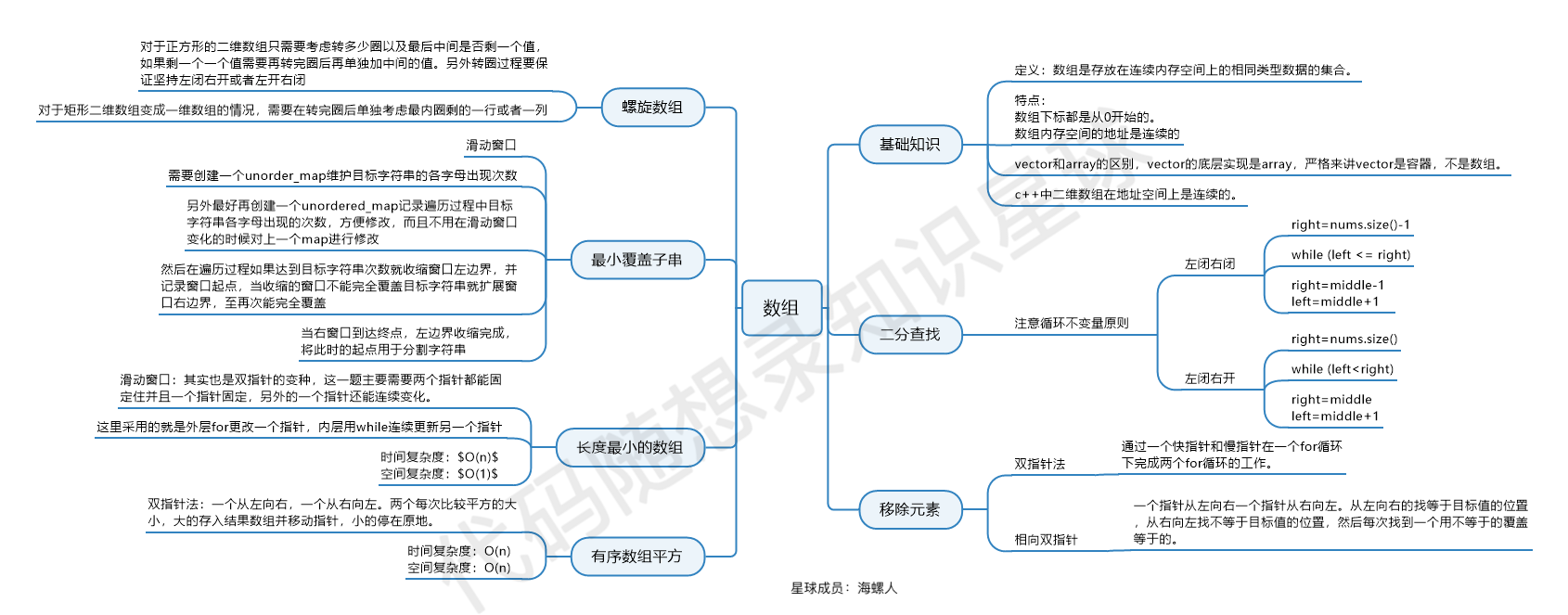
这个图是 代码随想录知识星球 (opens new window)成员:海螺人 (opens new window),所画,总结的非常好,分享给大家。
从二分法到双指针,从滑动窗口到螺旋矩阵,相信如果大家真的认真做了「代码随想录」每日推荐的题目,定会有所收获。
推荐的题目即使大家之前做过了,再读一遍文章,也会帮助你提炼出解题的精髓所在。











![[数据结构] 开散列法 闭散列法 模拟实现哈希结构](https://i-blog.csdnimg.cn/direct/2aa0817472f845928d56ebcfd9c88659.png)



