理论基础

什么是回溯法：递归函数下面通常有回溯法

它使用的地方：组合，切割，子集，排列，棋盘问题（N皇后，解数独）

回溯算法的模板:

void backtracking(参数)：
    #终止条件
    if (终止条件):
        收集结果
        return
    for (结合元素):
        处理节点
        递归函数
        回溯操作
    return

题目链接/文章讲解：代码随想录

视频讲解：带你学透回溯算法（理论篇）| 回溯法精讲！_哔哩哔哩_bilibili

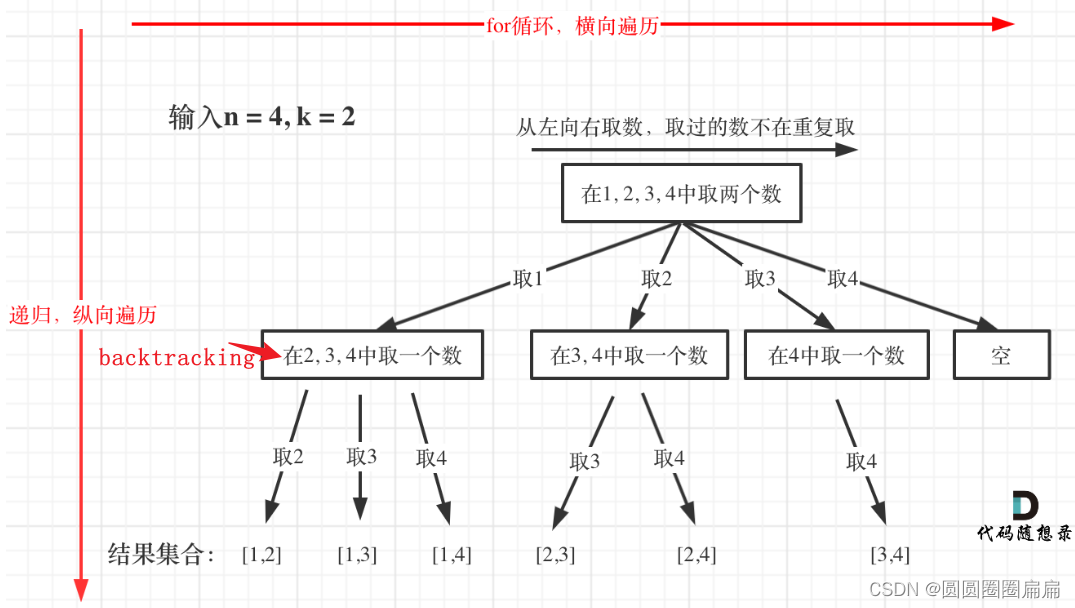
77. 组合

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        result = []
        temp = []
        def backtracking(n,k,startindex):
            nonlocal result,temp
            #如果两个元素了
            if len(temp) == k:
                #这里记得要加入的是temp[:]，而不是temp
                result.append(temp[:])
                return 
            for i in range(startindex,n+1):#控制树的横向遍历
                temp.append(i)
                backtracking(n,k,i+1)#递归：控制树的纵向遍历，注意下一层搜索要从i+1开始
                temp.pop()
        backtracking(n,k,1)
        return result
                

使用模板，可以很快的得出来，。这张图能画出来，就能写出来 

剪枝：

就是减去完全不符合条件的部分

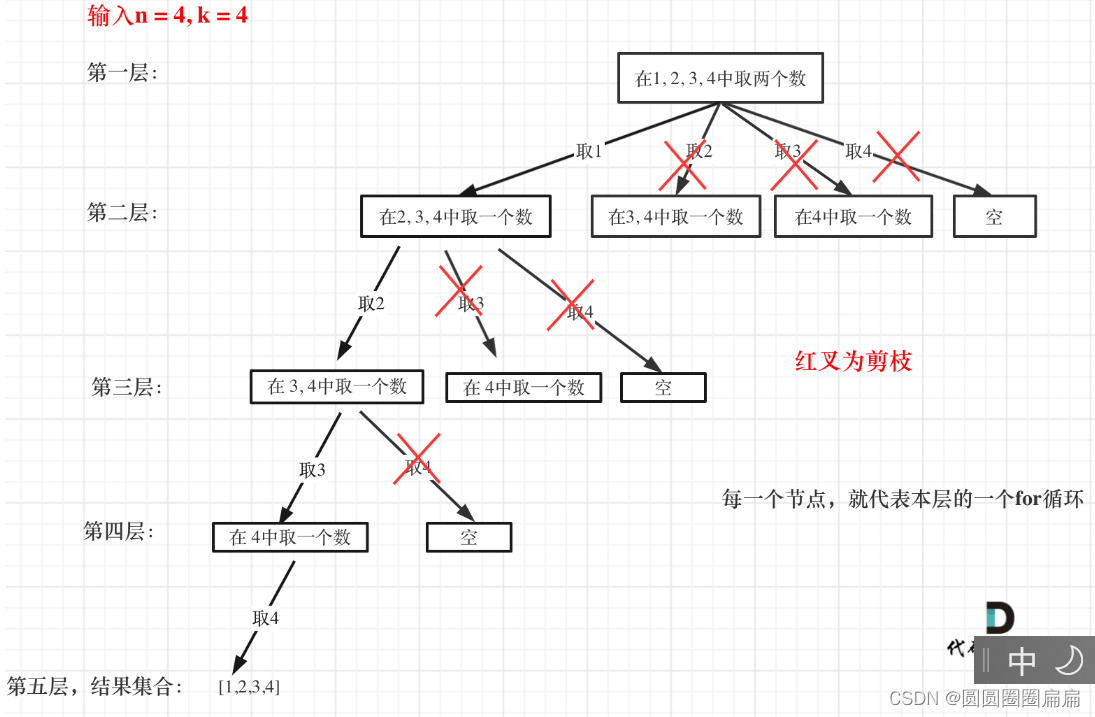
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了 

接下来看一下优化过程如下：

1. 已经选择的元素个数：path.size();

2. 还需要的元素个数为: k - path.size();

3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

题目链接/文章讲解：代码随想录

视频讲解：带你学透回溯算法-组合问题（对应力扣题目：77.组合）| 回溯法精讲！_哔哩哔哩_bilibili

剪枝操作：带你学透回溯算法-组合问题的剪枝操作（对应力扣题目：77.组合）| 回溯法精讲！_哔哩哔哩_bilibili