更加复杂的数据结构

一、引言

目前为止，我们接触了大量的数据结构，包括利用指针实现的三剑客和 C++ 自带的 STL 等。对于一些题目，我们不仅需要利用多个数据结果解决问题，还需要把这些数据结构进行嵌套和联动，进行更为复杂、更为快速的操作。

二、经典问题

1. 并查集

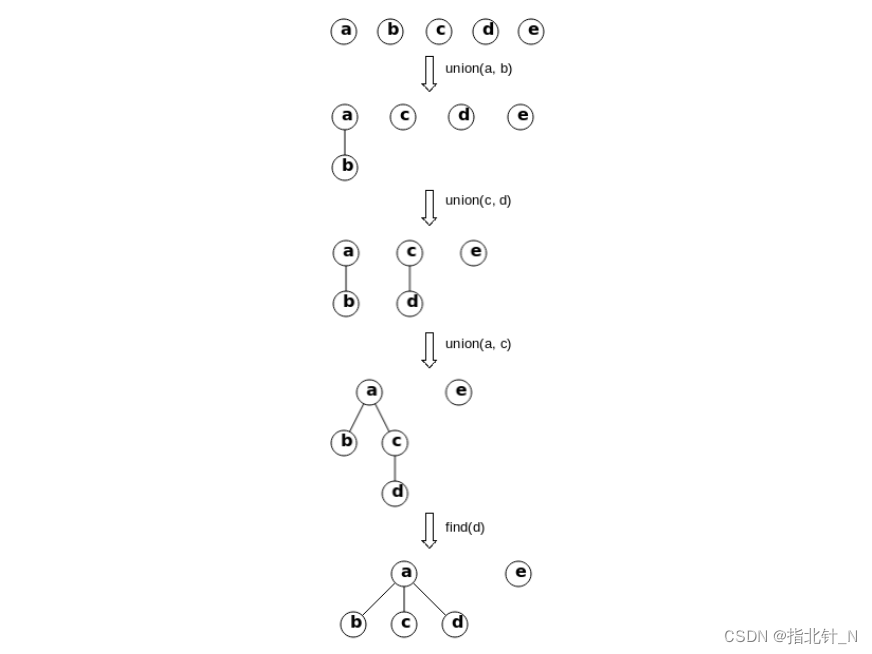
并查集（union-find, 或 disjoint set）可以动态地连通两个点，并且可以非常快速地判断两个点是否连通。假设存在 n 个节点，我们先将所有节点的父亲标为自己；每次要连接节点 i 和 j 时，我们可以将 i 的父亲标为 j；每次要查询两个节点是否相连时，我们可以查找 i 和 j 的祖先是否最终为同一个人。

并查集样例，其中 union 操作可以将两个集合连在一起，find 操作可以查找给定节点的祖先，并且如果可以的话，将集合的层数/高度降低

684. 冗余连接

684. Redundant Connection

树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

因为需要判断是否两个节点被重复连通，所以我们可以使用并查集来解决此类问题。具体实现算法如下所示。

class UF{
    vector<int> id;
public:
    UF(int n): id(n){
        // iota函数可以把数组初始化为0到n-1
        iota(id.begin(), id.end(), 0);
    }

    int find(int p){
        while(p != id[p]){
            p = id[p];
        }
        return p;
    }

    void connect(int p, int q){
        id[find(p)] = find(q);
    }

    bool isConnected(int p, int q){
        return find(p) == find(q);
    }
};

class Solution {
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        UF uf(n + 1);
        for(auto e: edges){
            int u = e[0], v= e[1];
            if(uf.isConnected(u, v)){
                return e;
            }
            uf.connect(u, v);
        }
        return vector<int>{-1, -1};
    }
};

为了加速查找，我们可以使用路径压缩和按秩合并来优化并查集。其具体写法如下所示。

class UF{
    vector<int> id, size;
public:
    UF(int n): id(n), size(n, 1){
        // iota函数可以把数组初始化为0到n-1
        iota(id.begin(), id.end(), 0);
    }

    int find(int p){
        while(p != id[p]){
            id[p] = id[id[p]];  // 路径压缩，使得下次查找更快
            p = id[p];
        }
        return p;
    }

    void connect(int p, int q){
        int i = find(p), j = find(q);
        // 按秩合并：每次合并都把深度较小的集合合并在深度较大的集合下面
        if(i != j){
            if(size[i] < size[j]){
                id[i] = j;
                size[j] += size[i];
            }else{
                id[j] = i;
                size[i] += size[j];
            }
        }
    }

    bool isConnected(int p, int q){
        return find(p) == find(q);
    }
};

2. 复合数据结构

这一类题通常采用 unordered_map 或 map 辅助记录，从而加速寻址；再配上 vector 或者 list 进行数据储存，从而加速连续选址或删除值。

146. LRU 缓存

146. LRU Cache

        请你设计并实现一个满足  LRU (最近最少使用) 缓存约束的数据结构。
实现 LRUCache 类：
        LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
        int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
        void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。
        函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

我们采用一个链表 list> 来储存信息的 key 和 value，链表的链接顺序即为最近使用的新旧顺序，最新的信息在链表头节点。同时我们需要一个嵌套着链表的迭代器的 unordered_map>::iterator> 进行快速搜索，存迭代器的原因是方便调用链表的 splice 函数来直接更新查找成功（cash hit）时的信息，即把迭代器对应的节点移动为链表的头节点。

class LRUCache {
    unordered_map<int, list<pair<int, int>>::iterator> hash;
    list<pair<int, int>> cache;
    int size;
public:
    LRUCache(int capacity): size(capacity) {
        
    }
    
    int get(int key) {
        auto it = hash.find(key);
        if(it == hash.end()){
            return -1;
        }
        cache.splice(cache.begin(), cache, it->second);
        return it->second->second;
    }
    
    void put(int key, int value) {
        auto it = hash.find(key);
        if(it != hash.end()){
            it->second->second = value;
            return cache.splice(cache.begin(), cache, it->second);
        }
        cache.insert(cache.begin(), make_pair(key, value));
        hash[key] = cache.begin();
        if(cache.size() > size){
            hash.erase(cache.back().first);
            cache.pop_back();
        }
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */