代码随想录Day 31|leetcode题目：56.合并区间、738.单调递增的数字、968.监控二叉树

提示：DDU，供自己复习使用。欢迎大家前来讨论~

文章目录

贪心算法Part05
题目
题目一：56. 合并区间
解题思路

题目二：738.单调递增的数字
解题思路：
暴力解法：结果超时
贪心算法

题目三： 968.监控二叉树
解题思路
确定遍历顺序
如何隔两个节点放一个摄像头

贪心章节总结

贪心算法Part05

回溯算法开始

题目

题目一：56. 合并区间

56. 合并区间

解题思路

判断区间重叠，区别就是判断区间重叠后的逻辑，本题是判断区间重叠后要进行区间合并。

先排序，让所有的相邻区间尽可能的重叠在一起，按左边界，或者右边界排序都可以，处理逻辑稍有不同。

按照左边界从小到大排序之后，如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界，则一定有重叠。（本题相邻区间也算重贴，所以是<=）

这么说有点抽象，看图：（注意图中区间都是按照左边界排序之后了）

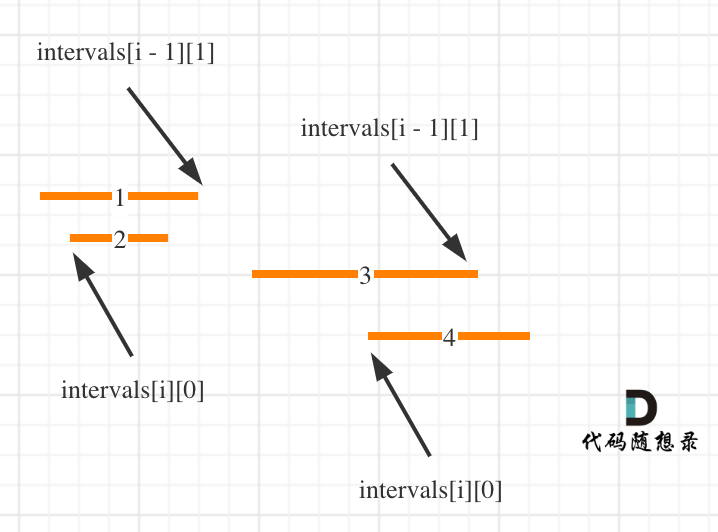
如何去模拟合并区间呢?

用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

完整的C++代码如下:

sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});

作用是对intervals这个容器中的元素按照每个元素的第一个值进行升序排序。在很多情况下，这种排序用于处理区间问题，其中每个区间由一对整数表示，第一个整数是区间的开始，第二个整数是区间的结束。通过这样的排序，可以方便地处理重叠区间等问题。

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> result;
        if (intervals.size() == 0) return result; // 区间集合为空直接返回
        // 排序的参数使用了lambda表达式
        sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});

        // 第一个区间就可以放进结果集里，后面如果重叠，在result上直接合并
        result.push_back(intervals[0]); 

        for (int i = 1; i < intervals.size(); i++) {
            if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间
                // 合并区间，只更新右边界就好，因为result.back()的左边界一定是最小值，因为我们按照左边界排序的
                result.back()[1] = max(result.back()[1], intervals[i][1]); 
            } else {
                result.push_back(intervals[i]); // 区间不重叠 
            }
        }
        return result;
    }
};

时间复杂度: O(nlogn)
空间复杂度: O(logn)，排序需要的空间开销

题目二：738.单调递增的数字

738. 单调递增的数字

解题思路：

暴力解法：结果超时

class Solution {
private:
    // 判断一个数字的各位上是否是递增
    bool checkNum(int num) {
        int max = 10;
        while (num) {
            int t = num % 10;
            if (max >= t) max = t;
            else return false;
            num = num / 10;
        }
        return true;
    }
public:
    int monotoneIncreasingDigits(int N) {
        for (int i = N; i > 0; i--) { // 从大到小遍历
            if (checkNum(i)) return i;
        }
        return 0;
    }
};

时间复杂度：O(n × m) m为n的数字长度
空间复杂度：O(1)

贪心算法

题目要求小于等于N的最大单调递增的整数，那么拿一个两位的数字来举例。

例如：98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]–，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数。

后面要考虑是从前向后遍历还是从后向前遍历呢？

从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。

这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。

那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299

确定了遍历顺序之后，那么此时局部最优就可以推出全局，找不出反例，试试贪心。

完整的C++代码如下:

class Solution {
public:
    int monotoneIncreasingDigits(int N) {
        string strNum = to_string(N);
        // flag用来标记赋值9从哪里开始
        // 设置为这个默认值，为了防止第二个for循环在flag没有被赋值的情况下执行
        int flag = strNum.size();
        for (int i = strNum.size() - 1; i > 0; i--) {
            if (strNum[i - 1] > strNum[i] ) {
                flag = i;
                strNum[i - 1]--;
            }
        }
        for (int i = flag; i < strNum.size(); i++) {
            strNum[i] = '9';
        }
        return stoi(strNum);//string 转换为 int
    }
};

时间复杂度：O(n)，n 为数字长度
空间复杂度：O(n)，需要一个字符串，转化为字符串操作更方便

小结：

理解特殊情况：考虑一个数字序列，如98，当出现一个数比它右边的数小（即非单调递增）时，我们希望减少左边的数并使右边的数变为9，从而得到一个更小的数（例如89）。
贪心策略：通过这个特殊情况，我们可以推导出一个贪心算法，即在遇到非单调递增的情况时，总是尝试减少较大的数并增加较小的数，以获得更小的整数。
遍历顺序：为了有效地应用这个贪心策略，我们需要从序列的末尾开始向前遍历。这样做可以确保我们能够利用之前比较的结果，避免重复计算。
代码实现技巧：在实现算法时，可以使用一个标志（flag）来记录从哪个位置开始需要将数字赋值为9。

题目三： 968.监控二叉树

968. 监控二叉树

解题思路

本题目要从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！

局部最优推出全局最优，找不出反例，那么就按照贪心来！

大体思路就是从底到上，先给叶子节点的父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。

此时这道题目还有两个难点：

二叉树的遍历
如何隔两个节点放一个摄像头

确定遍历顺序

从底向上推导：使用后序遍历也就是左右中的顺序，这样就可以在回溯的过程中从下到上进行推导了。

//后序遍历的代码
int traversal(TreeNode* cur) {

    // 空节点，该节点有覆盖
    if (终止条件) return ;

    int left = traversal(cur->left);    // 左
    int right = traversal(cur->right);  // 右

    逻辑处理                            // 中
    return ;
}

如何隔两个节点放一个摄像头

来看看这个状态应该如何转移，先来看看每个节点可能有几种状态：

有如下三种：

该节点无覆盖
本节点有摄像头
本节点有覆盖

我们分别有三个数字来表示：

0：该节点无覆盖
1：本节点有摄像头
2：本节点有覆盖

大家应该找不出第四个节点的状态了。

// 空节点，该节点有覆盖
if (cur == NULL) return 2;

递归的函数，以及终止条件已经确定了，再来看单层逻辑处理。

主要有如下四类情况：

情况1：左右节点都有覆盖

左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。

如图：

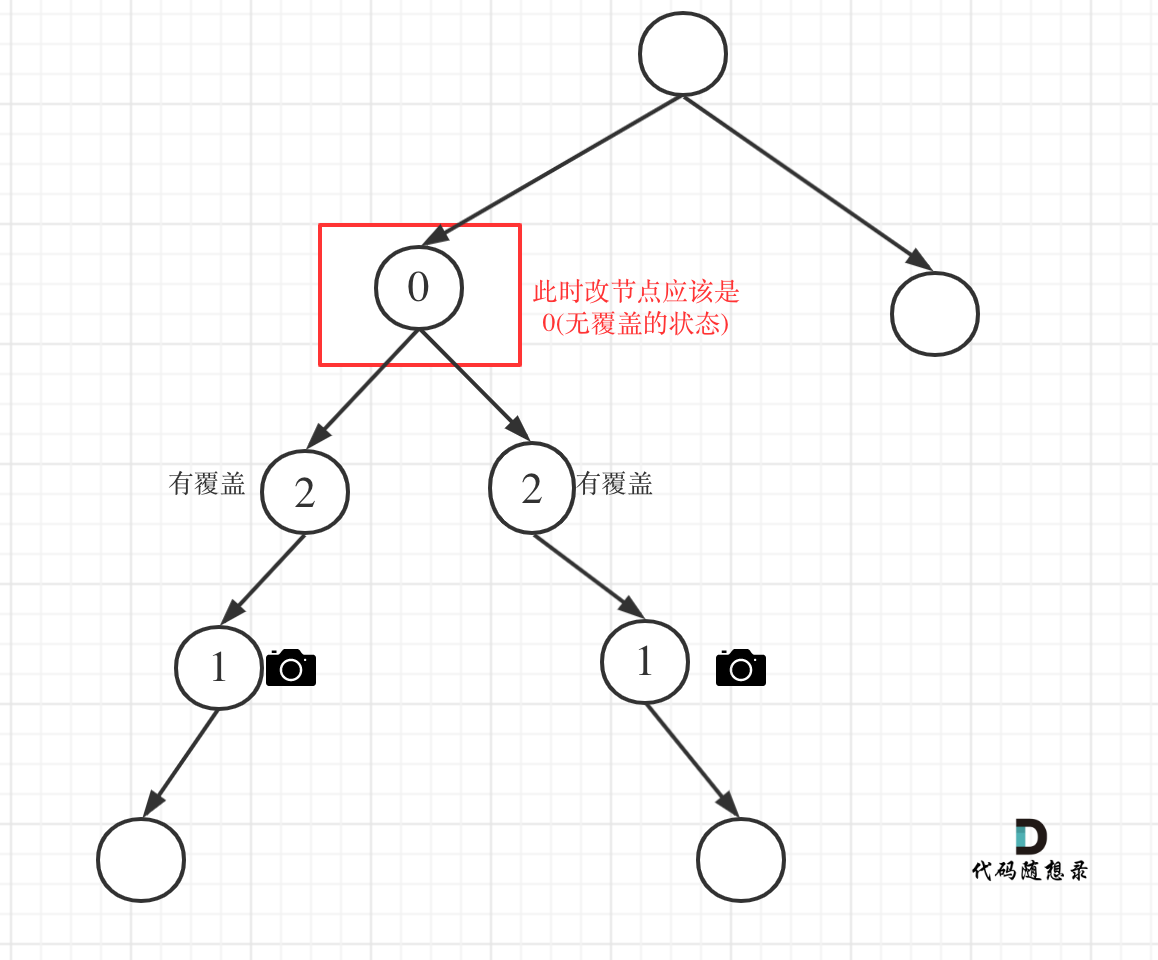
// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;

情况2：左右节点至少有一个无覆盖的情况

如果是以下情况，则中间节点（父节点）应该放摄像头：

left == 0 && right == 0 左右节点无覆盖
left == 1 && right == 0 左节点有摄像头，右节点无覆盖
left == 0 && right == 1 左节点有无覆盖，右节点摄像头
left == 0 && right == 2 左节点无覆盖，右节点覆盖
left == 2 && right == 0 左节点覆盖，右节点无覆盖

有一个孩子没有覆盖，父节点就应该放摄像头。

此时摄像头的数量要加一，并且return 1，代表中间节点放摄像头。

本题是多个集合求组合，所以在回溯的搜索过程中，都有一些细节需要注意的。

if (left == 0 || right == 0) {
    result++;
    return 1;
}

情况3：左右节点至少有一个有摄像头

if (left == 1 || right == 1) return 2;

情况4：头结点没有覆盖（这个是最后遍历完所有的才能知道）

以上都处理完了，递归结束之后，可能头结点还有一个无覆盖的情况，如图：

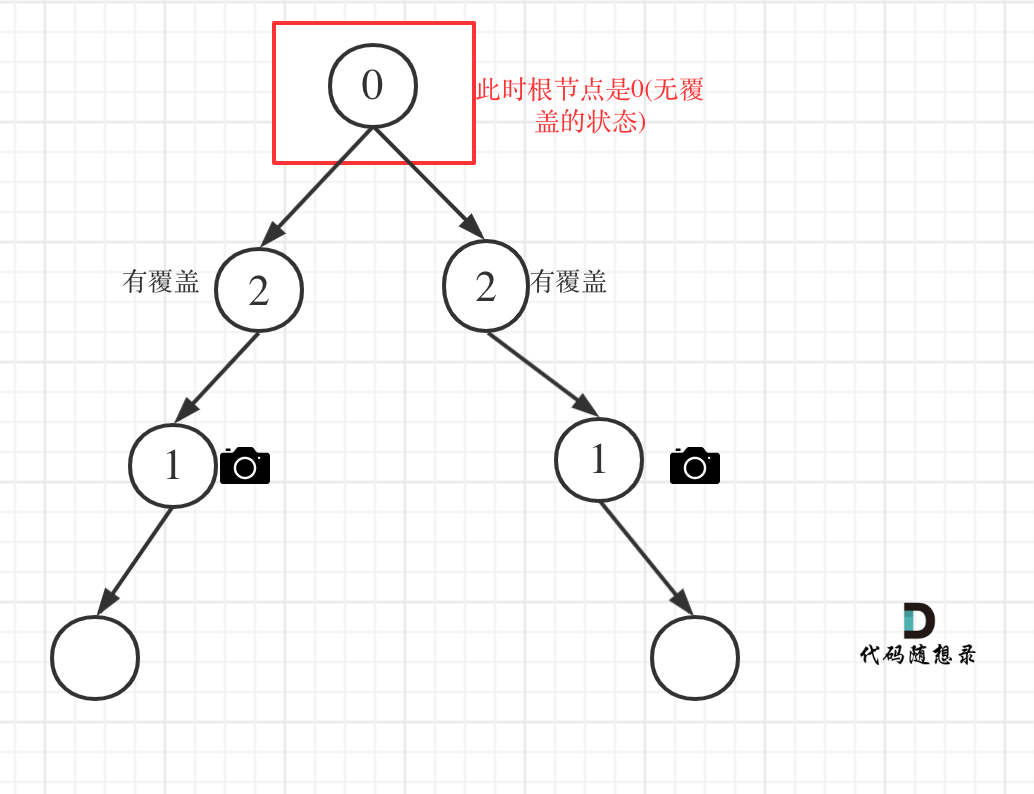
所以递归结束之后，还要判断根节点，如果没有覆盖，result++，代码如下：

int minCameraCover(TreeNode* root) {
    result = 0;
    if (traversal(root) == 0) { // root 无覆盖
        result++;
    }
    return result;
}

C++代码如下：

// 版本一
class Solution {
private:
    int result;
    int traversal(TreeNode* cur) {

        // 空节点，该节点有覆盖
        if (cur == NULL) return 2;

        int left = traversal(cur->left);    // 左
        int right = traversal(cur->right);  // 右

        // 情况1
        // 左右节点都有覆盖
        if (left == 2 && right == 2) return 0;

        // 情况2
        // left == 0 && right == 0 左右节点无覆盖
        // left == 1 && right == 0 左节点有摄像头，右节点无覆盖
        // left == 0 && right == 1 左节点有无覆盖，右节点摄像头
        // left == 0 && right == 2 左节点无覆盖，右节点覆盖
        // left == 2 && right == 0 左节点覆盖，右节点无覆盖
        if (left == 0 || right == 0) {
            result++;
            return 1;
        }

        // 情况3
        // left == 1 && right == 2 左节点有摄像头，右节点有覆盖
        // left == 2 && right == 1 左节点有覆盖，右节点有摄像头
        // left == 1 && right == 1 左右节点都有摄像头
        // 其他情况前段代码均已覆盖
        if (left == 1 || right == 1) return 2;

        // 以上代码我没有使用else，主要是为了把各个分支条件展现出来，这样代码有助于读者理解
        // 这个 return -1 逻辑不会走到这里。
        return -1;
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        // 情况4
        if (traversal(root) == 0) { // root 无覆盖
            result++;
        }
        return result;
    }
};

在以上代码的基础上，再进行精简，代码如下：

// 版本二
class Solution {
private:
    int result;
    int traversal(TreeNode* cur) {
        if (cur == NULL) return 2;
        int left = traversal(cur->left);    // 左
        int right = traversal(cur->right);  // 右
        if (left == 2 && right == 2) return 0;
        else if (left == 0 || right == 0) {
            result++;
            return 1;
        } else return 2;
    }
public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        if (traversal(root) == 0) { // root 无覆盖
            result++;
        }
        return result;
    }
};

时间复杂度: O(n)，需要遍历二叉树上的每个节点
空间复杂度: O(n)