1 背景

        为什么提出Frenet坐标系？Frenet坐标系的提出主要是为了解决自动驾驶系统在路径规划的问题，它基于以下几个原因：

1. 符合人类的驾驶习惯： 人类驾驶员在驾驶过程中，通常不会关心自己距离起点的横向和纵向距离，而是会关注车辆相对于道路的相对位置，比如与车道线的距离。Frenet坐标系提供了一种与人类驾驶习惯相符的描述方式，使得自动驾驶系统能够更好地模拟人类的驾驶行为。

2. 简化路径规划问题： 在笛卡尔坐标系中，路径规划需要考虑车辆在平面上的x和y坐标，这对于复杂的道路环境和曲线形的路径来说较为复杂。而Frenet坐标系是基于曲线的几何特性，将路径规划问题转化为沿曲线的纵向位置（弧长s）和横向偏移（偏移量d），这使得规划过程更加直观和简化。

3. 便于描述车辆运动： Frenet坐标系能够自然地描述车辆在曲线形道路上的运动，如车辆在曲线车道上的转向和定位。通过曲率和挠率的参数化，可以更容易地处理车辆在曲线上的运动学和动力学特性。

4. 适应不同的道路形状： 道路可以是直线也可以是曲线，Frenet坐标系可以适应任何形状的参考线。这使得自动驾驶系统可以处理各种道路条件，包括高速公路、城市道路和乡村小路等。

5. 提供有效的避障和车道变换策略： 在自动驾驶中，避障和车道变换是关键功能。Frenet坐标系提供了一种描述车辆与障碍物相对位置的有效方法，使得系统能够规划出避开障碍物或进行车道变换的最佳路径。

6. 减少计算复杂性： 由于Frenet坐标系直接基于曲线的几何属性，因此在计算曲率、挠率等参数时，可以减少计算量，提高系统的实时性。

        Frenet坐标系的提出是为了使自动驾驶系统在处理复杂的道路条件和车辆运动时更加高效、准确，同时与人类驾驶员的驾驶习惯相吻合。这种坐标系在自动驾驶领域得到了广泛应用，并成为了路径规划算法中的一个重要组成部分。

2 Frenet坐标系介绍

        Frenet坐标系是一种在几何学和物理学中常用的坐标系，它是由法国数学家Jean Frédéric Frenet在19世纪提出的，因此在数学和工程领域被广泛使用，特别是在轨迹规划和机器人控制中。以下是关于Frenet坐标系的详细介绍：

（1）定义

• Frenet坐标系基于一个参考线建立，该参考线可以是任意曲线，但在自动驾驶运动规划中通常定义为道路的中心线。
• 使用参考线的切线向量和法线向量建立一个直角坐标系，即Frenet坐标系。

（2）组成

• 曲线（法线）：Frenet坐标系中的曲线通常被称为“法线”，它是坐标系的基础。
• 正交平面：与法线垂直的两个平面构成正交平面，用于描述物体在曲线上的运动。

（3）坐标轴

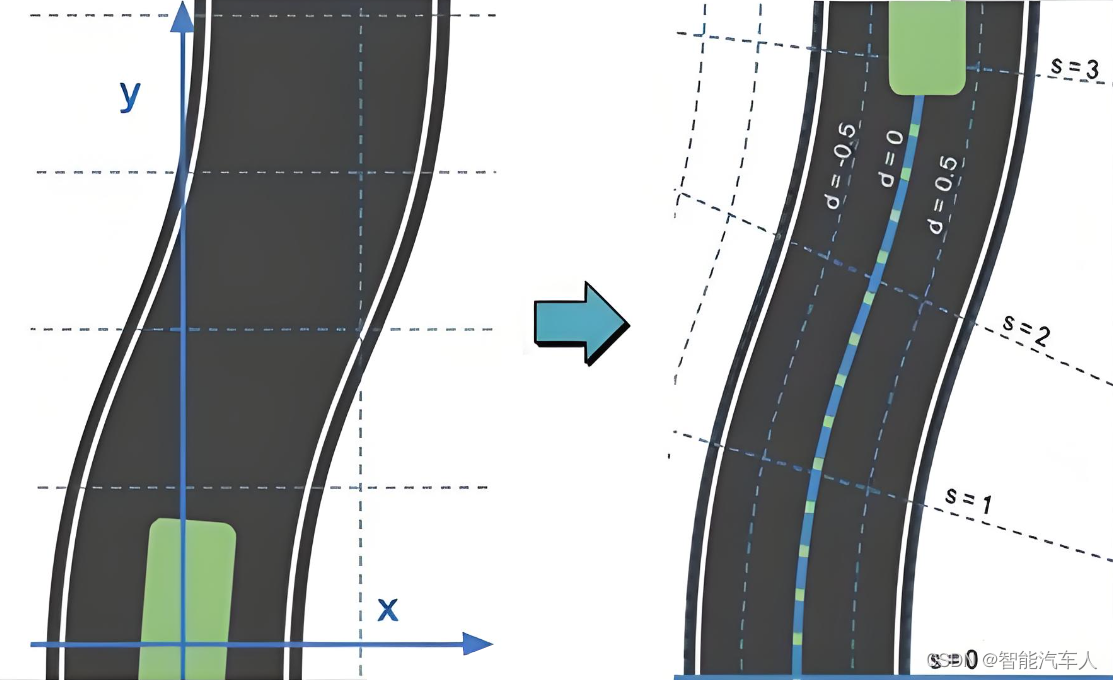
• s轴（纵轴）：纵坐标s值指的是参考线上的原点（车辆质心到参考线的投影点）与起点之间曲线的长度，即车辆在道路上的纵向行驶距离。
• d轴（横轴）：横坐标d值指的是原点与车辆质心之间的距离，即车辆偏离道路中心线的距离。

（4）特性

1. 移动性：由于车辆质心随时间不断变化，Frenet坐标系的原点也在不断变换，因此它是一个移动坐标系。
2. 直观性：在Frenet坐标系中，横轴和纵轴相互垂直且原点所在参考线与车道中心线平行，容易确定车辆偏离车道中心线的距离以及车辆沿车道中心线的行驶距离。
3. 简化问题：相比于笛卡尔坐标系，Frenet坐标系可以简化运动规划问题。在Frenet坐标系中，车辆的二维运动问题被解耦成两个一维运动问题，即纵向运动和横向运动，这使得问题更容易求解。

（5）应用

• Frenet坐标系在自动驾驶、飞行器导航与控制、机器人轨迹规划等领域有广泛应用。
• 它可以用于分析物体在曲线上运动的物理学问题，如车辆在曲道上的运动等。

（6）其他概念

• 曲率半径：曲线的曲率半径是曲线的最小弯曲半径。
• 弯角：曲线的弯角是指曲线从一条直线转向到另一条直线所需要的角度。

3 总结

        Frenet坐标系是一种基于参考线的移动坐标系，用于解决在轨迹规划和机器人控制中遇到的问题。它通过定义s轴和d轴来直观描述物体在曲线上的位置和姿态，并简化运动规划问题。由于其直观性和简化性，Frenet坐标系在多个领域得到广泛应用。