二分查找【算法 09】

news2024/12/25 12:42:54

二分查找算法详解

请添加图片描述

二分查找（Binary Search）是一种高效的查找算法，前提是数据必须是有序的。相比于线性查找，二分查找的时间复杂度从 O(n) 降低到了 O(log n)，适合处理大规模的数据查找问题。本文将详细介绍二分查找的原理、实现以及其时间复杂度分析。

1. 二分查找的基本原理

二分查找的核心思想是 “分而治之”。它每次通过将查找范围缩小一半，逐步接近目标值。

步骤如下：

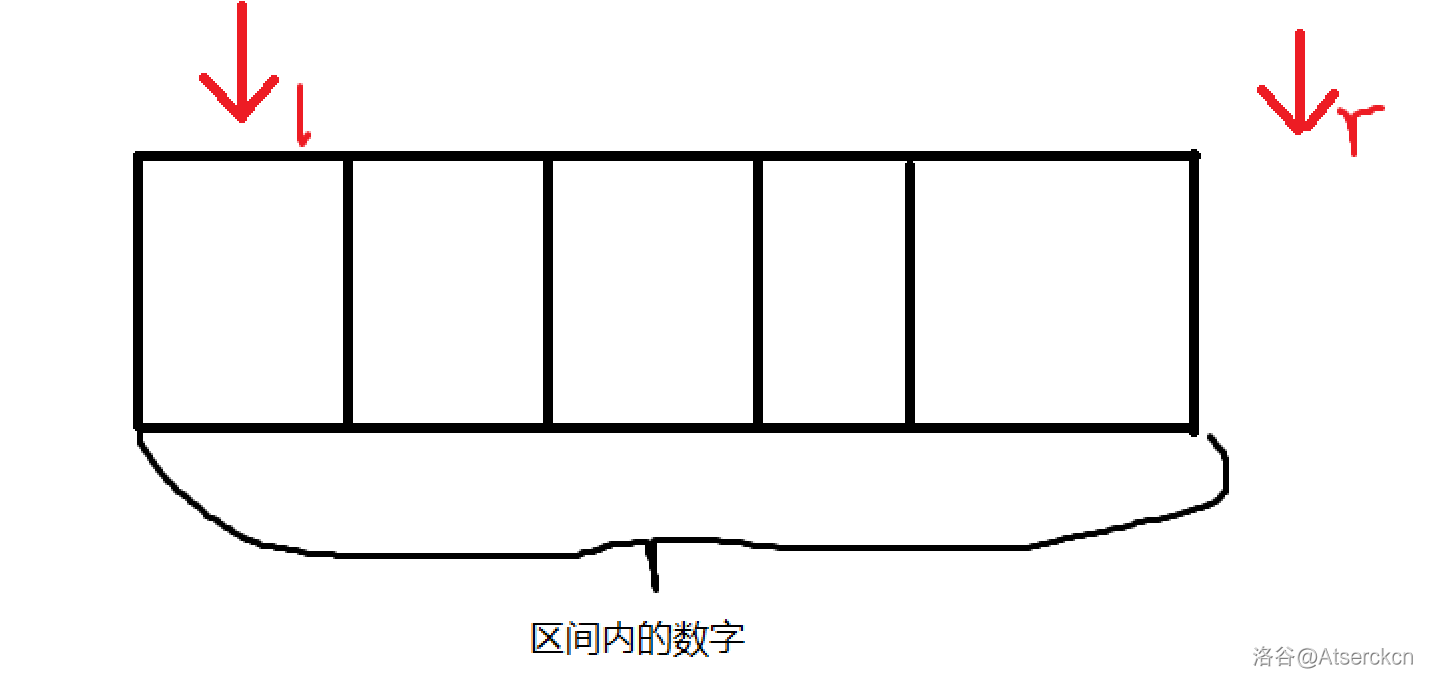
将查找范围的左右边界分别设为 low 和 high。
计算中间索引 mid，mid = (low + high) / 2。
比较目标值与 mid 位置的值：
- 如果目标值等于中间值，查找成功，返回索引。
- 如果目标值小于中间值，将 high 更新为 mid - 1，查找范围缩小为左半部分。
- 如果目标值大于中间值，将 low 更新为 mid + 1，查找范围缩小为右半部分。
重复上述步骤，直到 low > high，查找结束。如果没有找到，返回 -1 表示目标不存在。

2. 二分查找的代码实现

以下是用 C 语言实现的二分查找算法：

#include <stdio.h>

int binarySearch(int arr[], int size, int target) {
    int low = 0;
    int high = size - 1;

    while (low <= high) {
        int mid = low + (high - low) / 2;

        // 检查中间值是否为目标值
        if (arr[mid] == target)
            return mid;

        // 如果目标值小于中间值，缩小查找范围到左半部分
        if (arr[mid] > target)
            high = mid - 1;
        // 否则缩小查找范围到右半部分
        else
            low = mid + 1;
    }

    // 如果找不到目标值，返回 -1
    return -1;
}

int main() {
    int arr[] = {2, 3, 4, 10, 40};
    int size = sizeof(arr) / sizeof(arr[0]);
    int target = 10;
    int result = binarySearch(arr, size, target);
    if (result == -1)
        printf("Element is not present in array\n");
    else
        printf("Element is present at index %d\n", result);
    return 0;
}

代码说明：

low 和 high 分别表示查找的范围。
mid 用于找到中间元素，并根据该元素与目标值的比较结果决定查找范围的缩小方向。
算法的时间复杂度为 O(log n)，因为每次查找都会将查找空间减半。

3. 二分查找的递归实现

除了迭代实现外，二分查找还可以使用递归方式实现：

int binarySearchRecursive(int arr[], int low, int high, int target) {
    if (low <= high) {
        int mid = low + (high - low) / 2;

        // 检查中间值是否为目标值
        if (arr[mid] == target)
            return mid;

        // 如果目标值小于中间值，递归搜索左半部分
        if (arr[mid] > target)
            return binarySearchRecursive(arr, low, mid - 1, target);

        // 否则递归搜索右半部分
        return binarySearchRecursive(arr, mid + 1, high, target);
    }

    // 如果找不到目标值，返回 -1
    return -1;
}

int main() {
    int arr[] = {2, 3, 4, 10, 40};
    int size = sizeof(arr) / sizeof(arr[0]);
    int target = 10;
    int result = binarySearchRecursive(arr, 0, size - 1, target);
    if (result == -1)
        printf("Element is not present in array\n");
    else
        printf("Element is present at index %d\n", result);
    return 0;
}