浅谈二分算法

二分

首先知道一下二分是什么。

二分，是一种快速处理大型数据的方法。基本逻辑是折半查找。

设有一个共有 $n$ 个数字的数组，要从中查询某个元素，就可以用二分查找。

注：这里的数组默认其成员数值具有单调性。这个点十分重要。

还记得小时候（我现在才新初一）跟同学玩过一个游戏（数字炸弹），当时玩得可欢了，一直以为是一个概率小游戏（其实确实有概率的成分），每局能玩上十几分钟。

但是现在学完信息学后，特别是学完二分后，对它有了一种快速解决的方法。

首先我们知道，设出题者所想的这个数字为 $x$，则 $x\in [1,100]$，这是我们玩的规则，不过大差不差。

那么很显然，因为 $1\sim 100$ 具有单调上升的性质，而我们又只需要查找一个数，暴力的求解方法是从 $1$ 尝试到 $100$，最坏情况下需要枚举 $100$ 次，十分漫长。

而我们可以想到，每次说出一个数 $y$，只要不是 $y=x$，就可以排除 $100-y+1$ 或 $y$​​ 个数（这取决于你猜的这个数是大了还是小了）。

那么我们就可以利用这个特性，假设共有 $n$ 个数字，每次都排除 $n÷2$ 个数字，这样最多经过 ${\log }_2^n$ 次后就可以结束游戏。

其实小学课本里就有类似的例子，是数学书里一个单元叫做 “ 找次品 ” 的数学问题（不知道的自己查），但那里是用 ${\log }_3^n$ 的时间，这里不再赘述。

双指针

双指针，顾名思义，就是运用两个变量 $l,r$​ 表示所求区间的左右端点，可以更加轻松地控制对答案有贡献的区间。

设所求元素为 $p$，序列为 $a$。

比如每次取个中点 $mid=\frac{(l+r)}{2}$，若 $p<a_{mid}$，则 $r\leftarrow mid$，左端点 $l$ 不变。将区间控制为 $[l,mid]$。

否则 $l\leftarrow mid+1$，将区间控制为 $[mid+1,r]$。

但这里问题就来了，区间为空的判定条件是 $l=r$ 还是 $l>r$ 呢？

二分查找的边界条件

枚举以下情况

• 闭区间

若你用的是闭区间，即 $[l,r]$，则判断条件即为 $l=r$，因为若 $l=r$，则 $[l,r]$ 其实就是 $[l,l]$ 或 $[r,r]$ ，就是一个数，答案也显然即为 $a_l$​。

示意图：

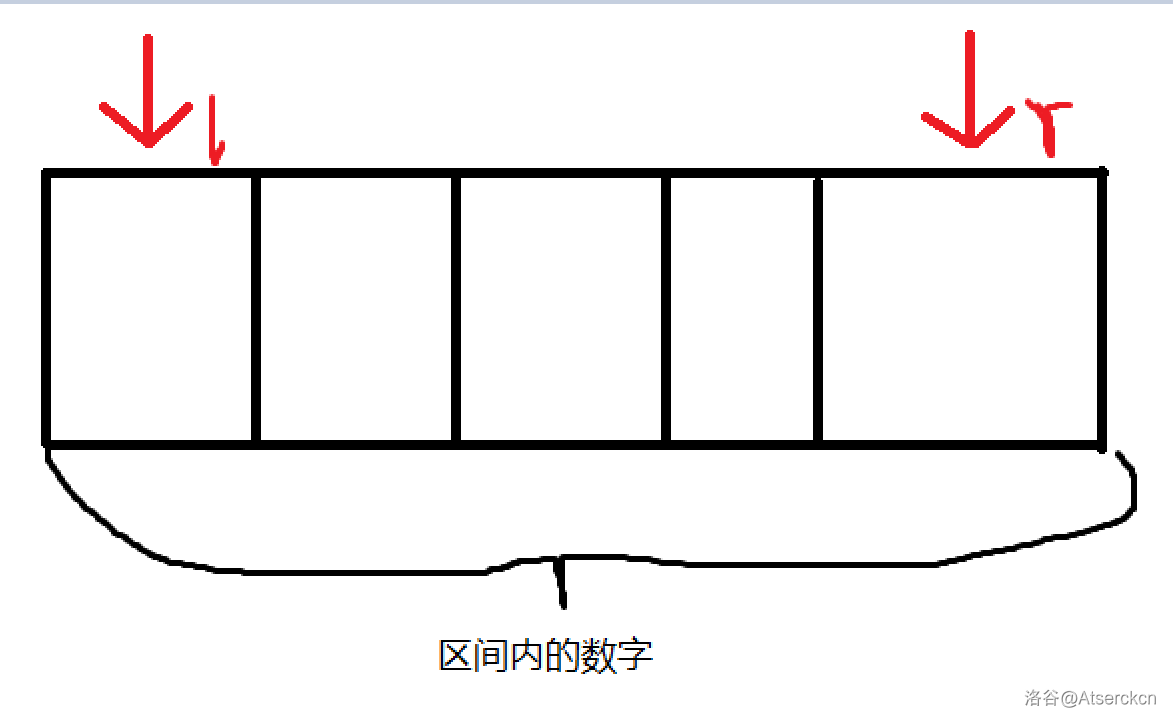
• 开区间

开区间，是 $(l,r)$，不包括 $l,r$ 。所以有效区间为 $[l+1,r-1]$。判断条件即为 $l+1=r-1$​。

示意图：

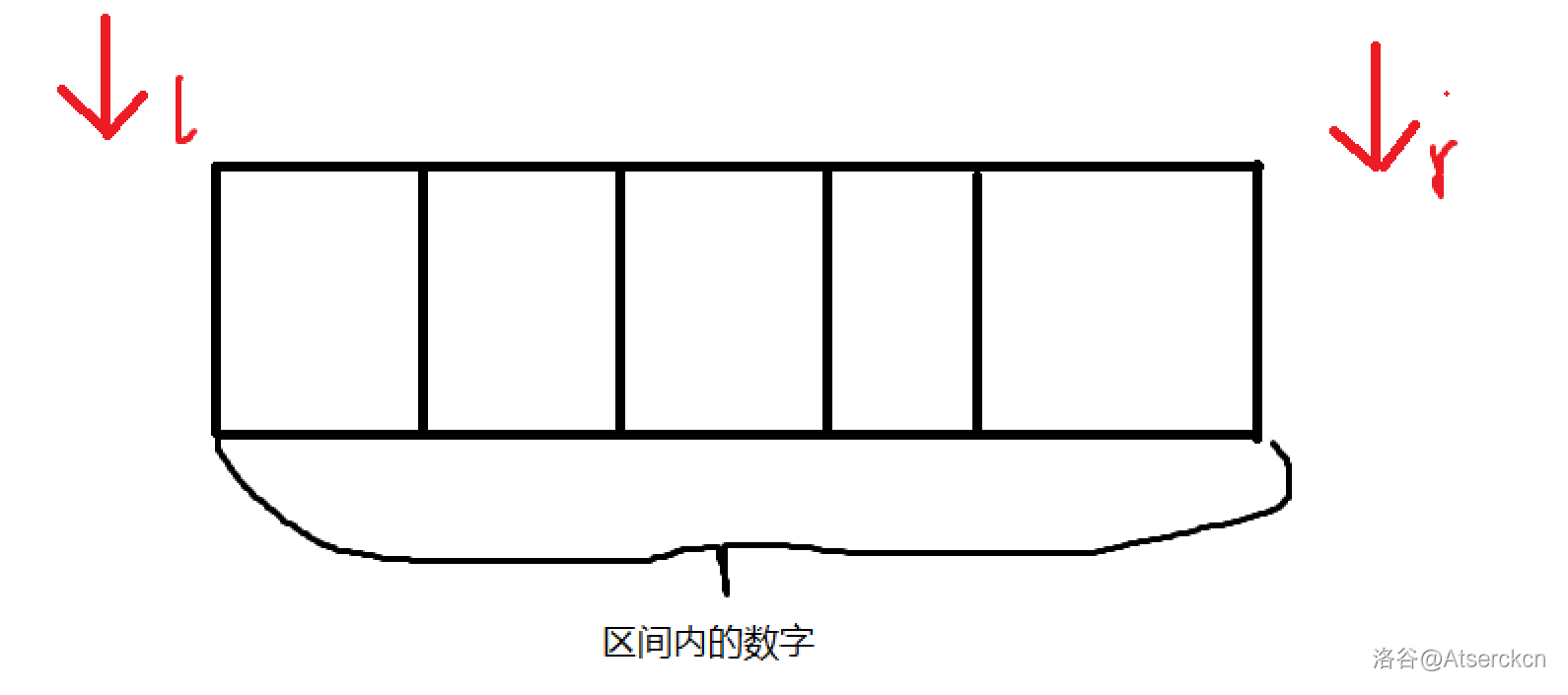
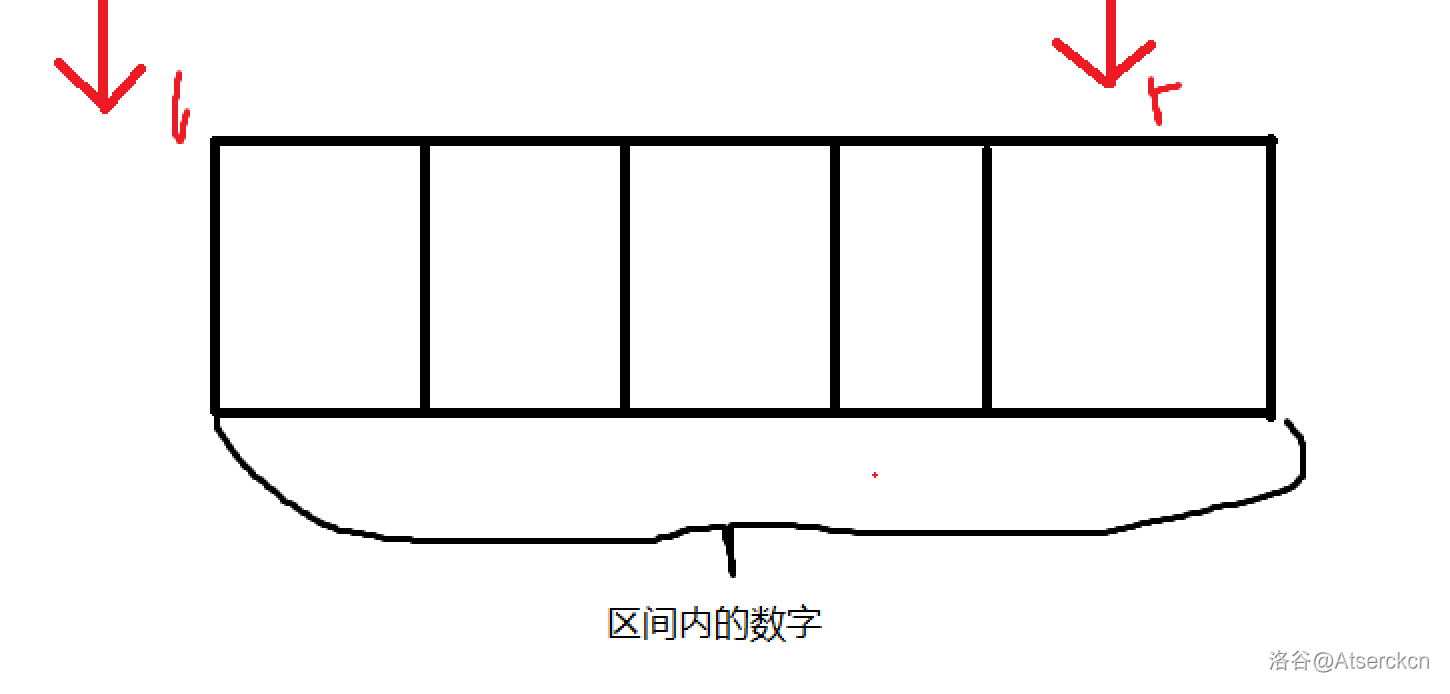
• 左开右闭

左开右闭，即 $(l,r]$ 有效区间为 $[l+1,r]$，边界条件即为 $l+1=r$​，还是就剩下一个数为止。

示意图：

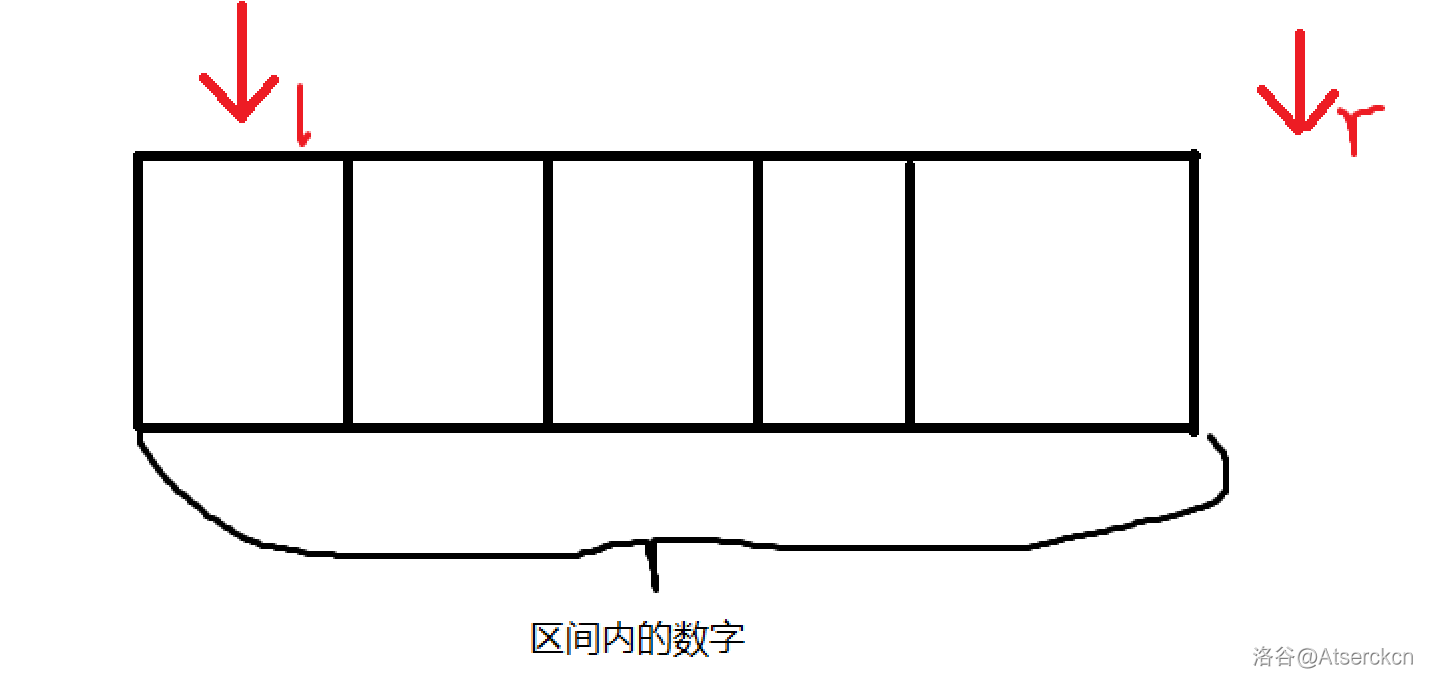
• 左闭右开

左闭右开，$[l,r)$，有效区间为 $[l,r-1]$，边界条件为 $l=r-1$​。

示意图：

所以可以总结一下，不管你的 $l,r$ 都表示什么意思，重点就是四个字，有效区间！

大概大家也注意到了，我在解释除了闭区间其他情况的时候，有效区间的左右端点都是用闭区间来表示，为什么呢？当然是因为我个人喜欢用闭区间啦。