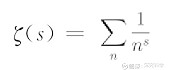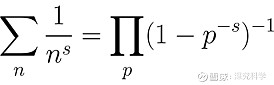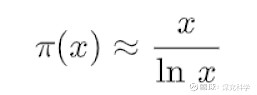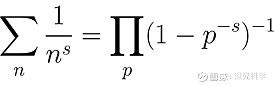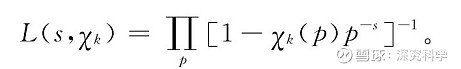目录
01
(1)这个级数实际上是s的函数,后来被称为ζ函数。
(2)证明了上面的结果,也就间接证明了 “素数无限多”,因为有限的序列之和不可能发散。
(3)等式左边的符号是与自然数n的幂次倒数有关的无穷求和,而右边的符号是遍历所有素数p的一个无穷乘积。这个公式通过复数s,将自然数n(n=1,2,3,4,5等)与素数p(p=2,3,5,7,11等)联系起来。
(4)上式是素数定理的粗略表达式,其中 ln x 为 x 的自然对数。
02
黎曼猜想,超越百年未解
03
张益唐和孪生素数猜想
04
广义黎曼猜想
原来对ζ函数的欧拉乘积公式(3):
05
朗道-西格尔零点问题
01
跨越千年,素数无限多吗?
素数是数论的研究对象,指的是只能被1和它自身整除的大于1的自然数。素数有无限多吗?分布情况如何?这些貌似简单的素数问题对数学家而言却魅力无穷。并且,这些简单问题牵涉甚广,素数分布问题的研究涉及到许多领域,推进了数学研究多方面的发展。
有关素数的第一个猜想应该是两千三百多年前的欧几里得提出的,称之为“素数无限多”的命题。欧几里得还给出了最简单的证明,用的是反证法。此外,古希腊还有一个在n不大的情况下实用的埃氏筛法,可以简单地把不大于根号n的所有素数的倍数剔除,从而 “筛出” 自然数n以内的全部素数,见下图。
图1 a)证明“素数无穷多”的反证法;b)埃氏筛法(n=18)
欧几里得之后差不多过了两千年,伟大的数学家欧拉(1707~1783)对素数问题作了很多工作,包括证明素数无限多,研究与素数分布相关的种种问题。例如,欧拉曾经研究如下的无穷级数:
(1)这个级数实际上是s的函数,后来被称为ζ函数。
欧拉一开始自然先考虑s为正整数的情况:当s=1时,得到的是我们熟悉的不收敛的调和级数;如s>1,级数收敛,比如:s=2,是欧拉解决的巴塞尔级数,无限项求和结果是ð2/6。
天才的欧拉将调和级数的发散性与“素数无限多”的问题联系起来,得到一个惊人的结论:所有素数的倒数之和,类似于调和级数一样地发散:
(2)证明了上面的结果,也就间接证明了 “素数无限多”,因为有限的序列之和不可能发散。
欧拉由此开始,通过研究ζ函数来研究质数,居然得到两者的神奇关系:ζ函数等于一个与所有质数相关的乘积!他得到下面这个看起来有点奇怪的“欧拉乘积公式”:
(3)等式左边的符号是与自然数n的幂次倒数有关的无穷求和,而右边的符号是遍历所有素数p的一个无穷乘积。这个公式通过复数s,将自然数n(n=1,2,3,4,5等)与素数p(p=2,3,5,7,11等)联系起来。
从欧拉乘积公式,可以间接地证明存在无穷多个素数。
如上所述,已有多种方法证明素数有无穷多个。但是,素数的出现规律却一直困惑着数学家。一个个地看,素数在正整数中的出现没有什么规律;可是总体地看,素数的个数竟然有规可循。
我们对付素数最笨的办法就是把它们从小到大一个一个列出来,如上图所示,列出了比100小的所有素数,的确看不出什么规律。然后,我们又想出一个笨主意:计数!数数看小于某一个数的素数有多少个?例如:小于10的素数有4个;小于20的素数有8个;小于50的素数有15个……
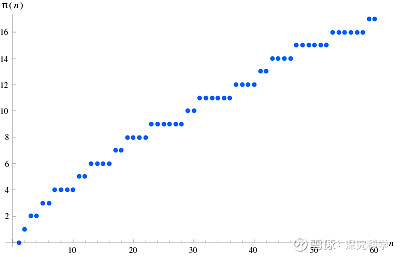
于是,数学家为此定义了一个函数,叫做素数计数函数,记作π(x),也就是说:π(10)=4;π(20)=8等等,可以一直估算下去。更进一步,可以把函数的图像画出来:
图2 素数计数函数
从π(x)的函数图,倒是研究出了一些素数个数增长的整体规律,称为“素数定理”:
(4)上式是素数定理的粗略表达式,其中 ln x 为 x 的自然对数。
公式的意思是,当x趋近无限,π(x)与x/ln x的比值趋近 1,但这不表示它们的数值随着x增大而接近。
素数分布的lnx倒数形式首先由欧拉猜想,勒让德最后得到素数定理。50年后,高斯在一封信中说他在少年时代就猜出了这个结果,所以素数定理也叫勒让德-高斯定理。
02
黎曼猜想,超越百年未解
高斯比欧拉要晚生70年,黎曼(1826-1866)是高斯的学生,可惜早逝于39岁。他思想深刻成果累累。据说当年高斯想试试黎曼到底有多聪明,让他从分析转做几何,没想到黎曼一上手便出人意料地创立了黎曼几何。之后,黎曼又继续欧拉没有完成的ζ函数研究素数问题。
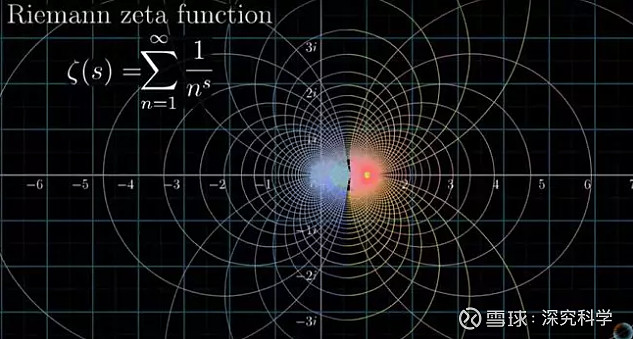
黎曼首先将欧拉的ζ函数(1)解析延拓到几乎整个复平面(除了s=1)。解析延拓的意思是将函数的定义域解析地扩大到原来不能应用的数域,即对所有的复数s,ζ函数都有定义,在S等于1的地方有一个不解析的、留数等于1的简单极点。
解析延拓后的ζ函数叫做 “黎曼ζ函数”。
黎曼ζ函数与素数有直接联系,根据欧拉乘积公式(3),当实部大于1时,它是一系列自然数幂次的倒数和,同时又是与所有素数有关的某种乘积。因此,通过对黎曼ζ函数的研究会得到很多素数方面的信息,例如素数定理(4),就是在1986年通过对黎曼ζ函数的研究而第一次被证明的。关于素数更精确的信息在于进一步对黎曼ζ函数零点的研究。
黎曼发现素数出现的频率与黎曼ζ函数的零点分布紧密相关。因此,黎曼研究ζ函数的零点分布。
1859年黎曼当选为柏林科学院通讯院士,他提交了八页纸论文《论小于某值的素数个数》。在文章中,他提出了黎曼猜想。这个猜想是数论中与素数相关至今未解的重要难题。
图3 黎曼ζ函数,将欧拉ζ函数解析延拓到整个复数平面
黎曼注意到,ζ函数的零点有两种。当s=-2、-4、-6、-8…(负偶数)时,是平凡零点,黎曼称其他零点为非平凡零点,素数频率与非平凡零点有关。非平凡零点到底在哪里呢?这个问题如此复杂,黎曼也没有准确的结论,因此他提出如下的“黎曼猜想”却没有证明——
所有的这些非平凡零点都在实部等于二分之一的那条垂直线上。
这一貌似轻松平淡的一个猜想,却令无数数学家们努力到如今,已经163年过去仍未解决,但也有所进展。从进展过程能看出这个问题的重要性、黎曼的深厚功夫和超凡的能力。
黎曼论文有三个命题:非平凡零点实部大于0但小于1;所有非平凡零点几乎都位于实部为1/2的直线上;黎曼ζ函数的所有非平凡零点都位于实部为1/2的直线上。
数学家46年后才对黎曼认为显而易见的第一命题给出证明;黎曼表示自己证明了第二命题,但没有简化到可以发表,然而迄今为止,第二第三命题都没有被证明出来;人们也试图寻找具体的非平凡零点,仍然十分困难。
猜想公布44年后,数学家第一次算出了前15个非平凡零点,又过了20年,算出了前138个零点,数学家西格尔在黎曼手稿中发现了73年前黎曼计算非平凡零点的一个公式(黎曼-西格尔公式)。西格尔找到这个公式后,4年内算出了1000多个非平凡零点。现在,数学家用这公式及计算机,验证了超过前200亿个非平凡零点。
迄今找到的所有零点,实部全部都是0.5,无一例外。
03
张益唐和孪生素数猜想
张益唐最近宣称的进展,便与上述的黎曼猜想相关。在介绍他在黎曼猜想的工作之前,先介绍他几年前有所突破的另一个素数问题:孪生素数猜想。
什么叫孪生素数?就是两个素数相差2,例如3和5;5和7等等。两千年前的欧几里得就证明了素数的个数是无穷多,同时,欧几里得也思考:孪生素数是否也有无穷多呢?欧几里得猜想是无穷多,但他没有给出证明,这就是孪生素数猜想——
“有无穷个素数对(p1, p2),满足p1-p2=2”
图4 孪生素数猜想
不过,张益唐并没有完全解决孪生素数猜想,他证明了什么呢?
为了理解张益唐的结果,首先,可以把孪生素数猜想写成:“存在无穷多个差值等于2的素数对”;而张益唐证明的是:“存在无穷多个差值小于7000万的素数对”。
也就是说,张益唐证明的是比原来猜想更 “弱”一点的命题。原来命题中的差距是2,但这个差距可以放宽,比如将间隔放宽到4,或者100、1000。张益唐的工作意味着:如果将间隔放宽到7000万,他就证明出来了。然后呢?然后可以再减小间隔缩小包围圈,如果能一直缩到2,就证明了原来的猜想!
以上是这种方法的思路。不过,比较一下这两个结论,你可能感到吃惊:7000万vs2,还差十万八千里呢!
的确如此,但在张益唐这个结论之前,这个问题还没有上限,即上限是无限大。而张益唐将无限大用有限数7000万代替,是里程碑式的进步。后来,陶哲轩等将此上限不断降低,张益唐提交证明之后,上限已降至246。
04
广义黎曼猜想
除了研究自然数中的素数分布之外,也有数学家研究算术(等差)级数中包含的素数。因为大于 2 的素数都是奇数,所以,等差数列 {1+2k,k=1, 2, 3…} 中包括了除了2之外的所有素数,换言之,上面等差数列中包含了无穷多个素数。
德国数学家狄利克雷(1805—1859)的 “狄利克雷定理”,说的就是关于算术级数中的素数问题。狄利克雷最早将解析的方法用于解决数论问题,称为解析数论。狄利克雷等在解析数论领域发展了一整套工具去研究某些函数的零点问题,应用于哥德巴赫猜想、孪生素数猜想等,也用于关于素数分布等问题上。
为了证明“狄利克雷定理”,狄利克雷1837年引进了狄利克雷L函数。狄利克雷L函数可以看作是黎曼ζ函数的推广:
比较黎曼ζ函数而言,狄利克雷L函数将求和中的每一项都乘了一个χ(n),称为狄利克雷特征。
狄利克雷特征χ(n)有下列性质:
•存在正整数k使得对于任意n都有χ(n) = χ(n+k);
•对于任意m,n,χ(mn) = χ(m) χ(n)
•χ(1)=1
第一条说明χ(n)是以k为周期循环的;第二条说明它是积性函数;第三条给出的χ(1)=1时,狄利克雷L函数成为黎曼ζ函数,保证了L函数的确是ζ函数的推广。用更为通俗的话来说:满足这三条性质的狄利克雷特征是一组函数χ(n),函数的定义域是自然数,值域可以被限制在只有三种可能:0, 1和-1。
因此,狄利克雷L函数与黎曼ζ函数不同的是,后者是一个函数,前者是一组(可以有无穷多个)函数,其中的一个特殊情况:狄利克雷特征全为1时,便简化为黎曼ζ函数。黎曼函数是狄利克雷L函数的特殊情况,也是最简单的一个情况。
狄利克雷L函数与黎曼ζ函数许多方面相似,可以互相对应。比如,狄利克雷L函数的零点也有平凡与非平凡之分,非平凡零点也全都位于0<Re(s)<1的带状区域(即临界带)内。对应于黎曼ζ函数的黎曼猜想,对应地便有狄利克雷L函数的广义黎曼猜想。
由于狄利克雷L函数是黎曼ζ函数的推广,因此广义黎曼猜想显然是黎曼猜想的推广。
黎曼猜想为黎曼ζ函数的所有非平凡零点都位于复平面上Re(s) = ½的直线上;广义黎曼猜想为狄利克雷L函数的所有非平凡零点都位于复平面上Re(s) = ½的直线上。如果证明了广义黎曼猜想,也就证明了黎曼猜想,反过来不成立。
原来对ζ函数的欧拉乘积公式(3):
对狄利克雷L函数,应该写成:
研究狄利克雷L函数的零点分布,不仅对于破解广义黎曼猜想和黎曼猜想有用,也可能对解决哥德巴赫猜想和孪生素数猜想等都有所帮助。
05
朗道-西格尔零点问题
黎曼猜想和广义黎曼猜想都尚未被证明,但大多数的数论学家都认为猜想是成立的,即ζ函数或L函数的所有非平凡零点都位于复平面上实部等于 ½的直线上。
朗道(1877-1938)和西格尔(1896-1981),是两位德国数学家,朗道是西格尔的导师。他们对狄利克雷L函数的非平凡零点进行了深入的研究,发现满足特殊性质时其对应的L函数可能出现位置异常的零点,难以避免。位置异常的意思是说,这种可能的零点不是位于实部1/2的那条直线上,而是在非常靠近1的地方。这种零点就被称为朗道-西格尔零点(或西格尔零点)。不过,他们也证明了对于狄利克雷L函数,这样的零点顶多只有一个,实部很接近1。
也就是说,“朗道-西格尔零点” 被定义为广义黎曼猜想的反例,而断言此类零点不存在的猜测就被称为朗道-西格尔猜想。如果这个朗道-西格尔零点真存在的话,广义黎曼假设就错了,所以事实上,数学家们努力探索西格尔零点问题,就是企图证明这样一个零点不存在。