【图论】Tarjan算法（强连通分量）

news2024/9/21 2:35:02

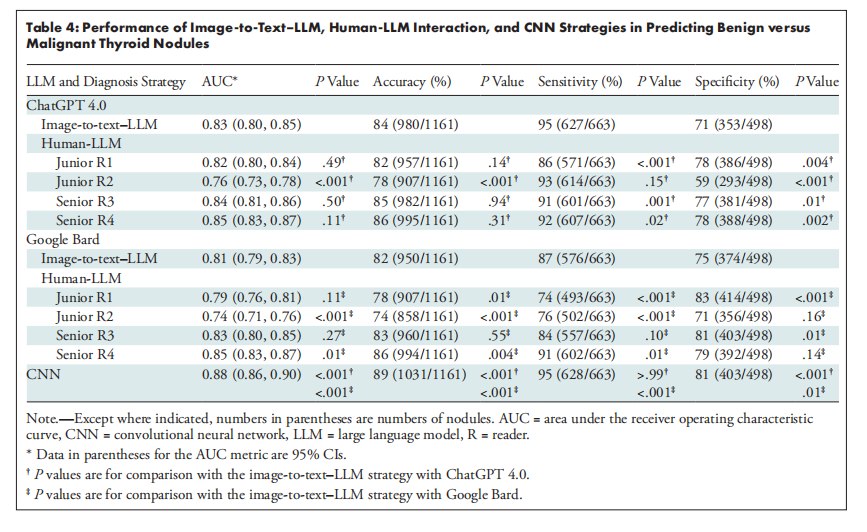
一、Tarjan算法简介

Tarjan算法是一种由美国计算机科学家罗伯特·塔杨（Robert Tarjan）提出的求解有向图强连通分量的线性时间的算法。

二、强连通分量的概念

在有向图 $G$ 中，如果任意两个不同的顶点相互可达，则称该有向图是强连通的。
如图1所示，图“郓城武安张”就是一个强连通图。

图1

如果在强连通图 $G$ 中进行加边操作得到有向图 $G^{'}$ ，那么我们称原图 $G$ 是 $G^{'}$ 的一个强连通分量。
如图2所示，图“郓城武安张”、图“同”和图“学”都是图“郓城武安张同学”的一个强连通分量。

图2

三、初识Tarjan算法

Tarjan算法本质上是基于深度优先搜索的一种算法。
在使用Tarjan算法时，需要用到两个辅助数组：
$dnf_x$ ：记录每个点被发现时的时刻。
$low_x$ ：表示以顶点x为根的子树中所有顶连出的边能到达的最早的能到达x的顶。
通俗一点，对于图2中的图，为了应对汉字无法作为下标的问题，我们简化一下，得到下面的图3。

图3

假定 $1$ 号结点为搜索起点，那么我们将有：

$dnf_i=\{1,2,3,4,5,6,7\}$
$low_i=\{1,1,1,1,1,6,7\}$

如果对上面的描述有疑惑，请往下看。

四、模拟Tarjan算法

我们继续看上面的图3，并对它进行模拟（假定 $1$ 号结点为搜索起点），深入地了解Tarjan算法。
为了帮助理解，求图3中的有向图以 $1$ 号结点为根的最小生成树，如图4。

图4

会发现，这棵树是一条链的结构。

初始化： $dnf_i=0$ ，对于每一步， $low_i=dnf_i$ ；
从 $1$ 号结点进入程序，并将其入栈，将 $dnf_1$ 的值赋为 $1$ ；
栈： $1$
$1$ 号结点可以直接到达 $2$ 号结点，且 $dnf_2=0$ ，将 $2$ 号结点入栈，并将将 $dnf_2$ 的值赋为 $2$ ；
栈： $12$
$2$ 号结点可以直接到达 $3$ 号结点，且 $dnf_3=0$ ，将 $3$ 号结点入栈，并将将 $dnf_3$ 的值赋为 $3$ ；
栈： $123$
$3$ 号结点可以直接到达 $4$ 号结点，且 $dnf_4=0$ ，将 $4$ 号结点入栈，并将将 $dnf_4$ 的值赋为 $4$ ；
栈： $1234$
$4$ 号结点可以直接到达 $5$ 号结点，且 $dnf_5=0$ ，将 $5$ 号结点入栈，并将将 $dnf_5$ 的值赋为 $5$ ；（注意啦，下一步是重点！）
栈： $12345$
$5$ 号结点可以直接到达 $1$ 号和 $6$ 号两个结点，按字典序先遍历 $1$ 号结点，因为 $dnf_1=1\neq0$ ，此时我们需要进行出栈操作；
栈： $12345$
将栈顶 $low_5$ 的值赋值为 $min(low_5,dnf_1)=1$ ，并将 $5$ 出栈，将栈顶 $low_4$ 的值赋值为 $min(low_4,dnf_5)=1$ ，并将 $4$ 出栈；
依此类推，直至 $1$ 被出栈；
栈：空
从 $5$ 号结点继续往下搜索， $5$ 号结点可以直接到达 $6$ 号结点，且 $dnf_6=0$ ，将 $6$ 号结点入栈，并将将 $dnf_6$ 的值赋为 $6$ ；
栈： $6$
$6$ 号结点可以直接到达 $7$ 号结点，且 $dnf_7=0$ ，将 $7$ 号结点入栈，并将将 $dnf_7$ 的值赋为 $7$ ；
栈： $67$
$7$ 号结点没有可以直接到达的结点，回溯（回溯过程省略）；
栈： $67$
此时，整个图都已经被搜索完毕，但是栈中仍存在原神元素，说明栈中剩余的每个结点都自成一个强连通分量，我们只需依次出栈即可。
栈：空
最终得到第三部分所提及的两个数组。

代码：

int step;
stack<int>st;
int dnf[300006],low[300006];
bool in_st[300006];
void tarjan(int x){
	int tmp;
	step++;
    dnf[x]=low[x]=step;
    st.push(u);
    in_st[x]=1;
    for(int i=head[x];i!=-1;i=nxt[i]){
        tmp=e[i];
        if(!dnf[tmp]){
            tarjan(tmp);
            low[x]=min(low[x],low[tmp]);
        }
        else if(in_st[tmp])low[x]=min(low[x],dnf[tmp]);
    }
    if(low[x]==dnf[x]){
        do{
            tmp=st.top();
            st.pop();
            in_st[tmp]=0;
        }while(tmp!=x);
    }
    return;
}