130124202408241009
DATE #:20240824
ITEM #:DOC
WEEK #:SATURDAY
DAIL #:捌月廿壹
TAGS< BGM = "风屿--闫东炜" > < theme = oi-graph theory > < [NULL] > < [空] > < [空] >``` 与风为名,屿之齐鸣。——风屿 ```
## LGV引理
LGV 引理,全称 Lindstrom-Gessel-Viennot lemma
用于求解DAG上的不相交路径数,也就是生成树数量
内容:
给出一个无向无权图,设 A 为邻接矩阵, D 为度数矩阵(D[i][i]=节点 i 的度数,其他的无值)。
则基尔霍夫(Kirchhoff)矩阵即为 : K=D−A
然后令 K′ 为 K 去掉第k行与第k列(k任意)的结果(n−1阶主子式),
det(K′) 即为该图的生成树个数。
容易理解 : 带重边的情况,上面的经典矩阵树定理也是能够处理的。
根据乘法原理,对于某种生成树的形态,其贡献为每条边重的次数的乘积。
如果把重边次数理解成权值的话,那么矩阵树定理求的就是 : 所有生成树边权乘积的总和。
(这里注意度数矩阵变成了相邻边的权值和)
前面都是无向图,神奇的是有向图的情况也是可以做的。
(邻接矩阵 A 的意义同有向图邻接矩阵)
那么现在的矩阵 D 就要变一下了。
若 D [ i ] [ i ] = ∑ j = 1 n A [ j ] [ i ] D[i][i]=\sum_{j=1}^nA[j][i] D[i][i]=∑j=1nA[j][i] ,即到该点的边权总和(入)。
此时求的就是外向树 (从根向外)
若 D [ i ] [ i ] = ∑ j = 1 n A [ j ] [ i ] D[i][i]=\sum_{j=1}^nA[j][i] D[i][i]=∑j=1nA[j][i] ,即从从该点出发的边权总和(出)。
此时求的就是内向树 (从外向根)
(如果考场上不小心忘掉了,可以手玩小样例)
(同样可以加权!)
此外,既然是有向的,那么就需要指定根。
前面提过要任意去掉第 k 行与第 k 列,是因为无向图所以不用在意谁为根。
在有向树的时候需要理解为指定根,结论是 : 去掉哪一行就是那一个元素为根。
(来自command_block)矩阵树定理(+行列式) - 洛谷专栏 (luogu.com.cn)
证明
略
P6178 [模板]Matrix-Tree 定理
【模板】Matrix-Tree 定理
题目描述
给定一张 n n n 个结点 m m m 条边的带权图(可能为无向图,可能为有向图)。
定义其一个生成树 T T T 的权值为 T T T 中所有边权的乘积。
求其所有不同生成树的权值之和,对 1 0 9 + 7 10^9+7 109+7 取模。
注意:
本题中,有向图的生成树指的是 以 1 1 1 为根的外向树;
两棵生成树 T 1 , T 2 T_1,T_2 T1,T2 不同,当且仅当存在存在一条边 e e e,满足 e ∈ T 1 , e ∉ T 2 e\in T_1,\ \ e\notin T_2 e∈T1, e∈/T2。
输入格式
第一行:三个整数 n , m , t n,m,t n,m,t,分别表示图的结点数量,边的数量和图的类型( t = 0 t=0 t=0 时为无向图, t = 1 t=1 t=1 时为有向图)。
接下来 m m m 行:每行三个整数 u , v , w u,v,w u,v,w。
如果 t = 0 t=0 t=0,表示 u , v u,v u,v 之间有一条权值为 w w w 的无向边;
如果 t = 1 t=1 t=1,表示从 u u u 到 v v v 有一条权值为 w w w 的有向边。
输出格式
第一行:一个整数 a n s ans ans,表示给定的图的生成树权值和对 1 0 9 + 7 10^9+7 109+7 取模的结果。
样例 #1
样例输入 #1
5 8 0 2 3 1 1 2 3 4 5 1 4 2 2 3 5 2 3 4 3 3 4 1 3 3 5样例输出 #1
144样例 #2
样例输入 #2
5 9 1 1 2 3 3 2 1 1 3 1 2 4 2 3 5 1 4 3 4 3 5 1 5 4 1 4 4 6样例输出 #2
72提示
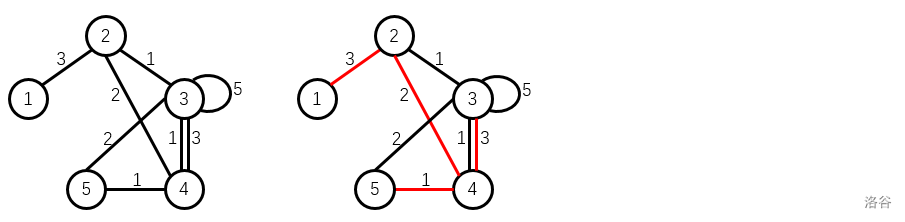
【样例 1 1 1 解释】
样例 1 1 1 中的无向图如左图所示:
右图为其一个权值为 3 × 1 × 2 × 3 = 18 3\times 1\times 2\times 3=18 3×1×2×3=18 的生成树的例子。
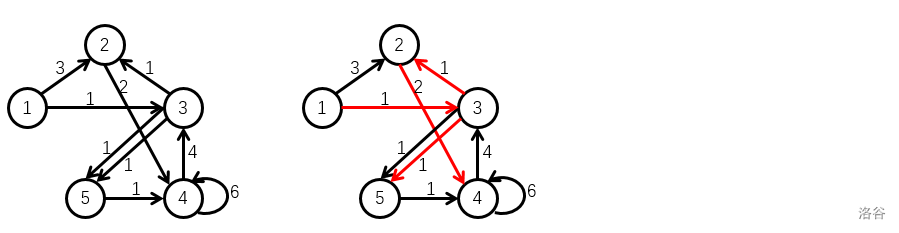
【样例 2 2 2 解释】
样例 2 2 2 中的有向图如左图所示:
右图为其一个权值为 1 × 1 × 1 × 2 = 2 1\times 1\times 1\times 2=2 1×1×1×2=2 的生成树(以 1 1 1 为根的外向树)的例子。
【数据范围】
对于 100 % 100\% 100% 的数据: 1 ≤ n ≤ 300 , 1 ≤ m ≤ 1 0 5 , t ∈ { 0 , 1 } , 1 ≤ u , v ≤ n , 1 ≤ w ≤ 1 0 9 1\leq n\leq 300,\ \ 1\leq m\leq 10^5,\ \ t\in \{0,1\},\ \ 1\leq u,v\leq n,\ \ 1\leq w\leq 10^9 1≤n≤300, 1≤m≤105, t∈{0,1}, 1≤u,v≤n, 1≤w≤109。
对于测试点 1 , 2 , 3 , 4 , 5 , 6 1,2,3,4,5,6 1,2,3,4,5,6, t = 0 t=0 t=0;对于测试点 7 , 8 , 9 , 10 , 11 7,8,9,10,11 7,8,9,10,11, t = 1 t=1 t=1。
图中 可能 存在重边和自环,重边算作多条边。
//2024.8.24
//by white_ice
//【模板】Matrix-Tree 定理 | P6178
//model
#include<bits/stdc++.h>
//ss#include"need.cpp"
using namespace std;
#define itn long long
#define int long long
constexpr int oo = 302;
constexpr itn mod = 1000000007;
itn n,m,t;
itn mp[oo][oo],out = 1;
__inline void lgv(){
itn flag = 1;
for (itn i=1;i<=n;i++){
for (itn j=i+1;j<=n;j++){
while (mp[j][i]){
itn p = mp[i][i]/mp[j][i];
for (itn k=i;k<=n;k++){
mp[i][k] = (mp[i][k]-p*mp[j][k]+mod)%mod;
swap(mp[i][k],mp[j][k]);
}
flag *= -1;
}
}
(out *= mp[i][i])%=mod;
}
out = (out*flag+mod)%mod;
}
main(void){
//fre();
cin.tie(0)->sync_with_stdio(0);
cin >> n >> m >> t;
for (itn a,b,c,i=1;i<=m;i++){
cin >> a >> b >> c; a--,b--;
if(!t){
mp[a][a] = (mp[a][a]+c)%mod;
mp[b][b] = (mp[b][b]+c)%mod;
mp[a][b] = (mp[a][b]-c+mod)%mod;
mp[b][a] = (mp[b][a]-c+mod)%mod;
}
else {
mp[b][b] = (mp[b][b]+c)%mod;
mp[b][a] = (mp[b][a]-c+mod)%mod;
}
}
n--;lgv();
cout << out << '\n';
exit(0);
}
P4336 [SHOI2016] 黑暗前的幻想乡
[SHOI2016] 黑暗前的幻想乡
题目背景
四年一度的幻想乡大选开始了,最近幻想乡最大的问题是很多来历不明的妖怪涌入了幻想乡,扰乱了幻想乡昔日的秩序。但是幻想乡的建制派妖怪(人类)博丽灵梦和八云紫等人整日高谈所有妖怪平等,幻想乡多元化等等,对于幻想乡目前面临的种种大问题却给不出合理的解决方案。
风见幽香是幻想乡里少有的意识到了问题严重性的大妖怪。她这次勇敢地站了出来参加幻想乡大选,提出包括在幻想乡边境建墙(并让人类出钱),大力开展基础设施建设挽回失业率等一系列方案,成为了大选年出人意料的黑马并顺利地当上了幻想乡的大统领。
题目描述
幽香上台以后,第一项措施就是要修建幻想乡的公路。幻想乡一共有 n n n 个城市,之前原来没有任何路。幽香向选民承诺要减税,所以她打算只修 n − 1 n-1 n−1 条公路将这些城市连接起来。但是幻想乡有正好 n − 1 n-1 n−1 个建筑公司,每个建筑公司都想在修路的过程中获得一些好处。虽然这些建筑公司在选举前没有给幽香钱,幽香还是打算和他们搞好关系,因为她还指望他们帮她建墙。所以她打算让每个建筑公司都负责一条路来修。
每个建筑公司都告诉了幽香自己有能力负责修建的路是哪些城市之间的。所以幽香打算 n − 1 n - 1 n−1 条能够连接幻想乡所有城市的边,然后每条边都交给一个能够负责该边的建筑公司修建,并且每个建筑公司都恰好修建一条边。
幽香现在想要知道一共有多少种可能的方案呢?两个方案不同当且仅当它们要么修的边的集合不同,要么边的分配方式不同。
输入格式
第一行包含一个整数 n n n,表示城市个数。
第 2 2 2 到第 n n n 行,第 ( i + 1 ) (i + 1) (i+1) 行表示 第 i i i 个建筑公司可以修建的路的列表:以一个非负整数 m i m_i mi 开头,表示其可以修建条路的条数;接下来有 m i m_i mi 对整数 u , v u, v u,v,每对数表示一条边的两个端点。其中不会出现重复的边,也不会出现自环。
输出格式
输出一行一个整数,表示所有可能的方案数对 1 0 9 + 7 10^9+7 109+7 取模的结果。
样例 #1
样例输入 #1
4 2 3 2 4 2 5 2 1 3 1 3 2 4 1 4 3 4 2 1 3 2 4 1 4 2样例输出 #1
17提示
数据规模与约定
- 对于 20 % 20\% 20% 的测试点, n ≤ 5 n \le 5 n≤5。
- 对于 50 % 50\% 50% 的测试点, n ≤ 8 n \le 8 n≤8。
- 对于 60 % 60\% 60% 的测试点, n ≤ 10 n \le 10 n≤10。
- 对于 100 % 100\% 100% 的测试点, 2 ≤ n ≤ 17 2 \leq n \le 17 2≤n≤17, 0 ≤ m i ≤ n ( n − 1 ) 2 0 \leq m_i \leq \frac{n(n - 1)}{2} 0≤mi≤2n(n−1), 1 ≤ u , v ≤ n 1 \leq u, v \leq n 1≤u,v≤n。
//2024.8.24
//by white_ice
//[SHOI2016] 黑暗前的幻想乡 | P4336
//LGV,容斥
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn long long
#define int long long
constexpr int oo = 20;
constexpr int mod = 1e9+7;
itn n,m;
itn mp[oo][oo];
vector<pair<int,int>> q[oo];
__inline int det(){
int out=1;
for(int i=1;i<=n;++i){
int p=-1;
for(int j=i;j<=n;++j)
if(mp[i][j]){p=j;break;}
if(!~p) return 0;
if(p!=i){swap(i,p);out*=-1;}
for(int j=i+1;j<=n;++j){
while(mp[j][i]){
int tmp=mp[j][i]/mp[i][i];
for(int k=i;k<=n;++k){
mp[j][k]-=1ll*tmp*mp[i][k]%mod;
mp[j][k]=(mp[j][k]%mod+mod)%mod;
}
if(!mp[j][i]){break;}
swap(mp[i],mp[j]);
out*=-1;
}
}
out=out*mp[i][i]%mod;
}
return out;
}
main(void){
//fre();
cin.tie(0)->sync_with_stdio(0);
cin >> n;n--;
for (itn x,y,i=1;i<=n;i++){
cin >> m;
while (m--){
cin >> x >> y;
q[i].push_back(make_pair(x,y));
}
}
itn out = 0;
for(int i=1;i<(1<<n);++i){
memset(mp,0,sizeof(mp));
int cnt=0;
for(int j=1;j<=n;++j){
if(!(i&(1<<(j-1)))){
continue;
}
++cnt;
for(int k=0;k<q[j].size();++k){
int x=q[j][k].first,y=q[j][k].second;
++mp[x][y],++mp[y][x];
--mp[x][x],--mp[y][y];
}
}
out=(out+((cnt&1)?-1:1)*det())%mod;
}
out = (out+mod)%mod;
cout << out << flush;
exit(0);
}
考虑当没有每个公司只能修一条路的限制,那么就直接计数,LGV求解生成树即可
观察数据范围,很难不发现,n很小,可以状压枚举每种选k个公司给方案
每次将枚举的公司所能修的路加入矩阵并求解生成树
之后考虑容斥解题,记 f i f_i fi为 k = i k=i k=i时可能的方案数
那么答案就是
∑
f
1
−
∑
f
2
+
∑
f
3
⋯
±
∑
f
n
\sum f_1-\sum f_2 +\sum f_3 \dots \pm \sum f_n
∑f1−∑f2+∑f3⋯±∑fn
当然,符号正负取决于选数个数的奇偶性
如此枚举即可