二叉搜索树算法实现原理
二叉搜索树(Binary Search Tree,简称BST)是一种节点有序排列的二叉树数据结构。它具有以下性质:
-
每个节点最多有两个子节点。
-
对于每个节点,其左子树的所有节点值都小于该节点值,其右子树的所有节点值都大于该节点值。
实现基本步骤和代码示例
步骤
-
定义节点类:包含节点值、左子节点和右子节点。
-
插入节点:递归或迭代地将新值插入到树中合适的位置。
-
搜索节点:根据节点值在树中查找特定值。
-
删除节点:从树中删除特定值的节点,并维护树的结构。
-
遍历树:包括前序遍历、中序遍历、后序遍历和层次遍历等。
完整代码示例
namespace HelloDotNetGuide.常见算法
{
public class 二叉搜索树算法
{
public static void BinarySearchTreeRun()
{
var bst = new BinarySearchTree();
// 插入一些值到树中
bst.Insert(50);
bst.Insert(30);
bst.Insert(20);
bst.Insert(40);
bst.Insert(70);
bst.Insert(60);
bst.Insert(80);
bst.Insert(750);
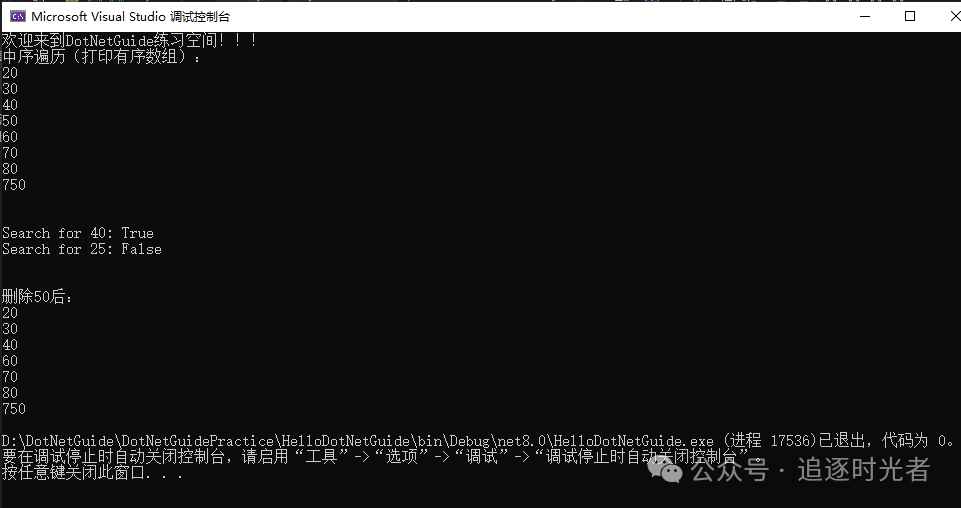
Console.WriteLine("中序遍历(打印有序数组):");
bst.InorderTraversal();
Console.WriteLine("\n");
// 查找某些值
Console.WriteLine("Search for 40: " + bst.Search(40)); // 输出: True
Console.WriteLine("Search for 25: " + bst.Search(25)); // 输出: False
Console.WriteLine("\n");
// 删除某个值
bst.Delete(50);
Console.WriteLine("删除50后:");
bst.InorderTraversal();
}
}
/// <summary>
/// 定义二叉搜索树的节点结构
/// </summary>
public class TreeNode
{
public int Value;
public TreeNode Left;
public TreeNode Right;
public TreeNode(int value)
{
Value = value;
Left = null;
Right = null;
}
}
/// <summary>
/// 定义二叉搜索树类
/// </summary>
public class BinarySearchTree
{
private TreeNode root;
public BinarySearchTree()
{
root = null;
}
#region 插入节点
/// <summary>
/// 插入新值到二叉搜索树中
/// </summary>
/// <param name="value">value</param>
public void Insert(int value)
{
if (root == null)
{
root = new TreeNode(value);
}
else
{
InsertRec(root, value);
}
}
private void InsertRec(TreeNode node, int value)
{
if (value < node.Value)
{
if (node.Left == null)
{
node.Left = new TreeNode(value);
}
else
{
InsertRec(node.Left, value);
}
}
else if (value > node.Value)
{
if (node.Right == null)
{
node.Right = new TreeNode(value);
}
else
{
InsertRec(node.Right, value);
}
}
else
{
//值已经存在于树中,不再插入
return;
}
}
#endregion
#region 查找节点
/// <summary>
/// 查找某个值是否存在于二叉搜索树中
/// </summary>
/// <param name="value">value</param>
/// <returns></returns>
public bool Search(int value)
{
return SearchRec(root, value);
}
private bool SearchRec(TreeNode node, int value)
{
// 如果当前节点为空,表示未找到目标值
if (node == null)
{
return false;
}
// 如果找到目标值,返回true
if (node.Value == value)
{
return true;
}
// 递归查找左子树或右子树
if (value < node.Value)
{
return SearchRec(node.Left, value);
}
else
{
return SearchRec(node.Right, value);
}
}
#endregion
#region 中序遍历
/// <summary>
/// 中序遍历(打印有序数组)
/// </summary>
public void InorderTraversal()
{
InorderTraversalRec(root);
}
private void InorderTraversalRec(TreeNode root)
{
if (root != null)
{
InorderTraversalRec(root.Left);
Console.WriteLine(root.Value);
InorderTraversalRec(root.Right);
}
}
#endregion
#region 删除节点
/// <summary>
/// 删除某个值
/// </summary>
/// <param name="val">val</param>
public void Delete(int val)
{
root = DeleteNode(root, val);
}
private TreeNode DeleteNode(TreeNode node, int val)
{
if (node == null)
{
return null;
}
if (val < node.Value)
{
node.Left = DeleteNode(node.Left, val);
}
else if (val > node.Value)
{
node.Right = DeleteNode(node.Right, val);
}
else
{
// 节点有两个子节点
if (node.Left != null && node.Right != null)
{
// 使用右子树中的最小节点替换当前节点
TreeNode minNode = FindMin(node.Right);
node.Value = minNode.Value;
node.Right = DeleteNode(node.Right, minNode.Value);
}
// 节点有一个子节点或没有子节点
else
{
TreeNode? temp = node.Left != null ? node.Left : node.Right;
node = temp;
}
}
return node;
}
/// <summary>
/// 找到树中的最小节点
/// </summary>
/// <param name="node"></param>
/// <returns></returns>
private TreeNode FindMin(TreeNode node)
{
while (node.Left != null)
{
node = node.Left;
}
return node;
}
#endregion
}
}
输出结果:
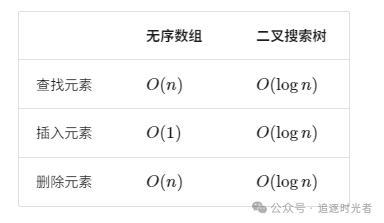
数组与搜索树的效率对比
二叉搜索树的各项操作的时间复杂度都是对数阶,具有稳定且高效的性能。只有在高频添加、低频查找删除数据的场景下,数组比二叉搜索树的效率更高。
二叉搜索树常见应用
-
用作系统中的多级索引,实现高效的查找、插入、删除操作。
-
作为某些搜索算法的底层数据结构。
-
用于存储数据流,以保持其有序状态。
C#数据结构与算法实战入门指南
-
https://mp.weixin.qq.com/s/XPRmwWmoZa4zq29Kx-u4HA
参考文章
-
https://www.hello-algo.com/chapter_tree/binary_search_tree
-
https://www.hello-algo.com/chapter_tree/binary_tree_traversal



















