全文链接:https://tecdat.cn/?p=37397
摘要:本文对医疗卫生、通信、金融、房地产和零售等行业的数据展开深入研究。通过读取数据、计算收益率、构建 VAR 模型并进行估计,帮助客户进一步分析各行业变量的影响及残差的协方差与相关矩阵(点击文末“阅读原文”获取完整代码数据)。
相关视频
同时,计算传统溢出效应并进行动态变化分析,以揭示这些行业之间的相互关系和动态影响。
引言
在当下瞬息万变且复杂多元的经济格局中,不同行业间的相互关联与影响已然成为理解宏观经济运行的关键所在。各个行业并非孤立存在,它们之间存在着错综复杂的联系,这些联系不仅影响着单个行业的发展态势,更在宏观层面上对整个经济体系的稳定与增长发挥着至关重要的作用。本研究聚焦于医疗卫生、通信、金融、房地产和零售这五个具有代表性的行业,旨在运用 VAR 模型等先进的计量经济学方法,深度挖掘它们之间内在的关联机制以及动态变化规律,为相关政策的制定和经济决策提供有力的理论支持和实证依据。
读取数据
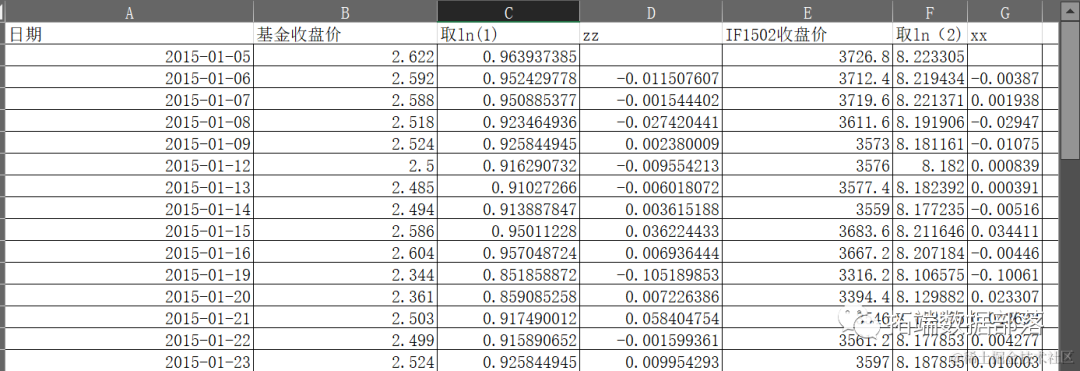
读取每个板块的日指数数据。
#读取数据data=read.xlsx("总.xlsx",startRow=2 )#查看部分数据head(data)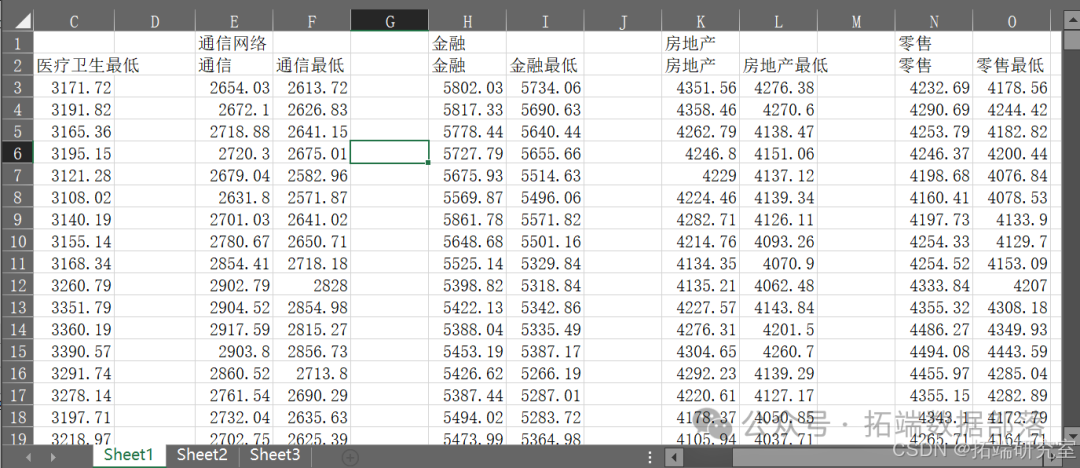
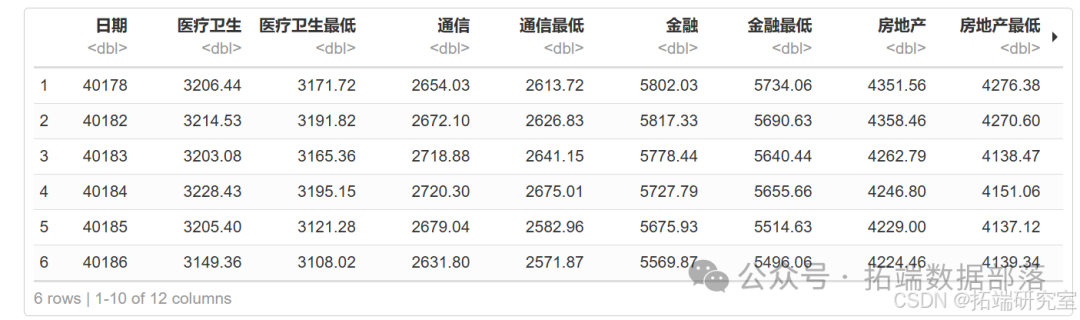
#计算收益率for(i in 1:ncol(data))data\[,i\] =c(NA,diff(data\[,i\] )/data\[,i\]\[-length(data\[,i\] )\])计算具有常数的 VAR (2) 估计值并保存结果
est <- VAR(exlSim, p = 2, type = "const") 


plot(est)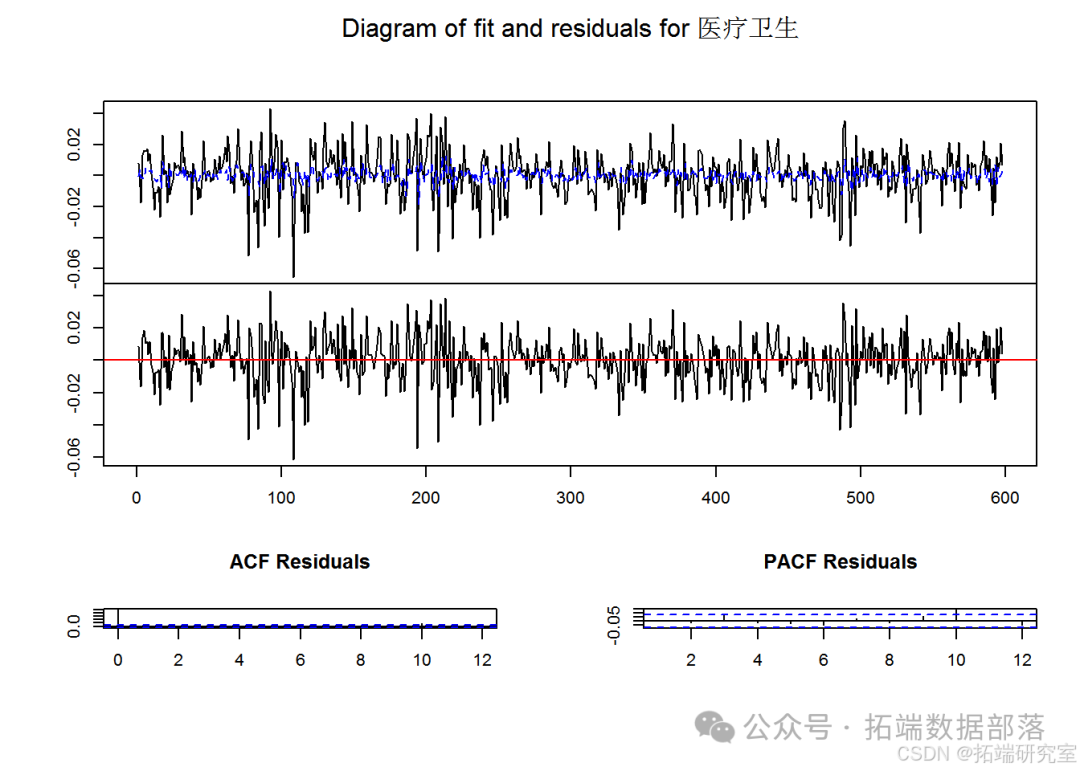
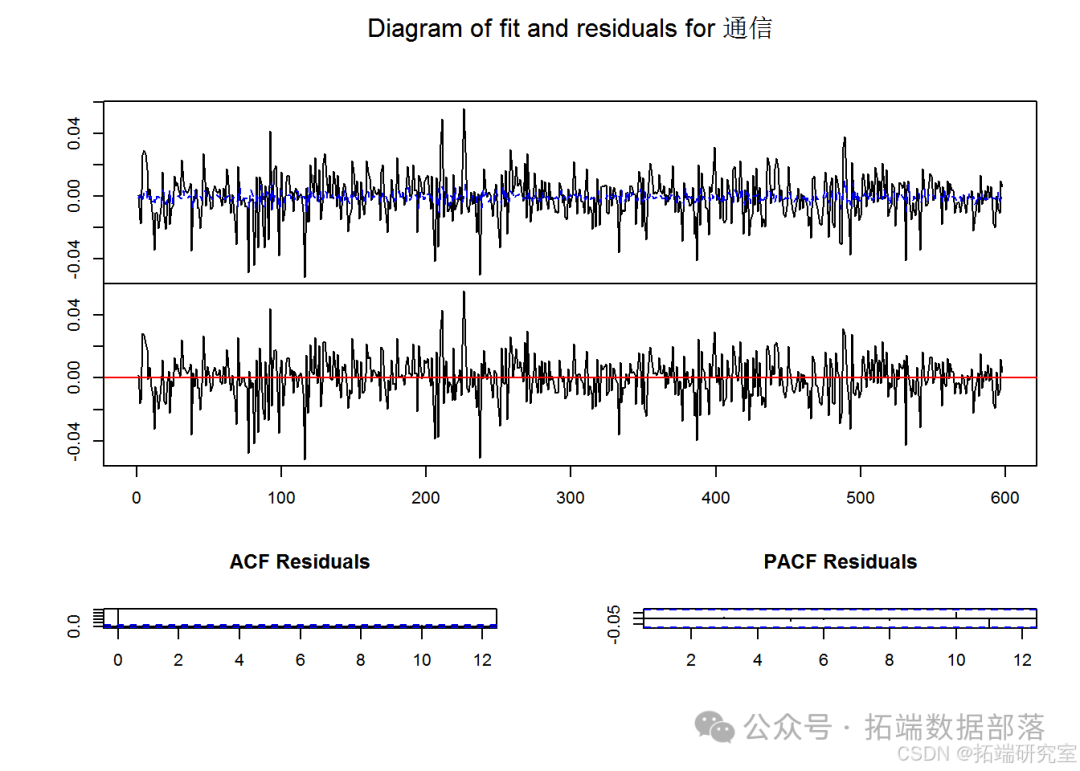
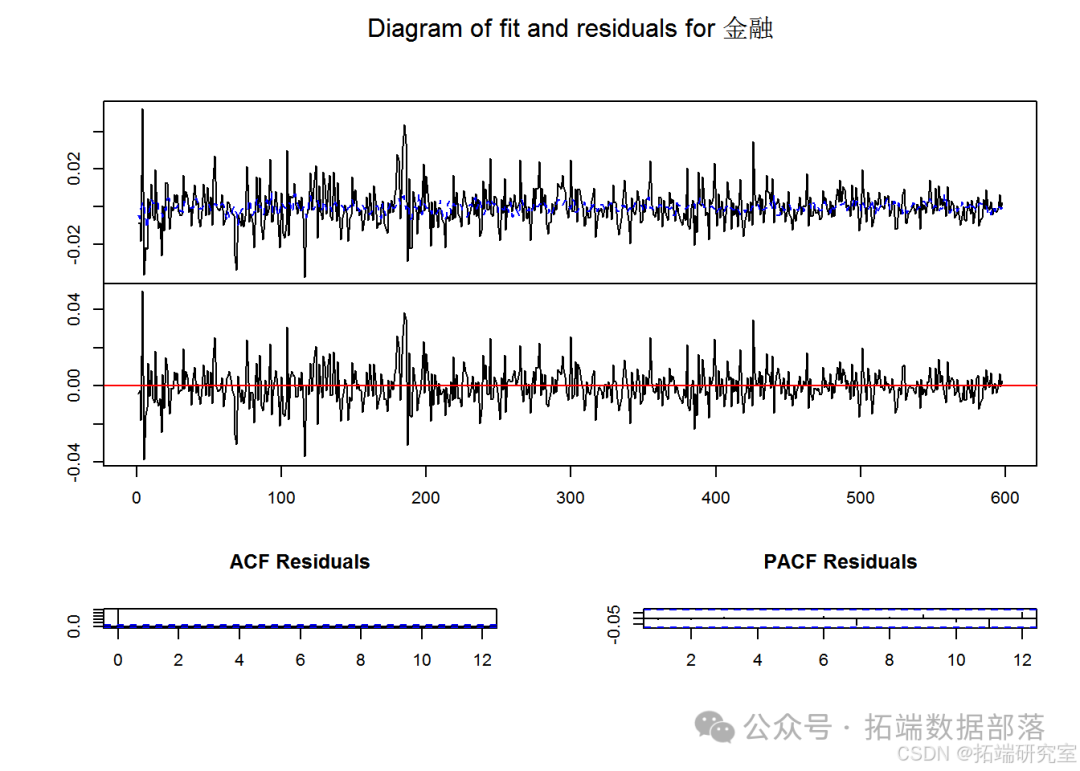
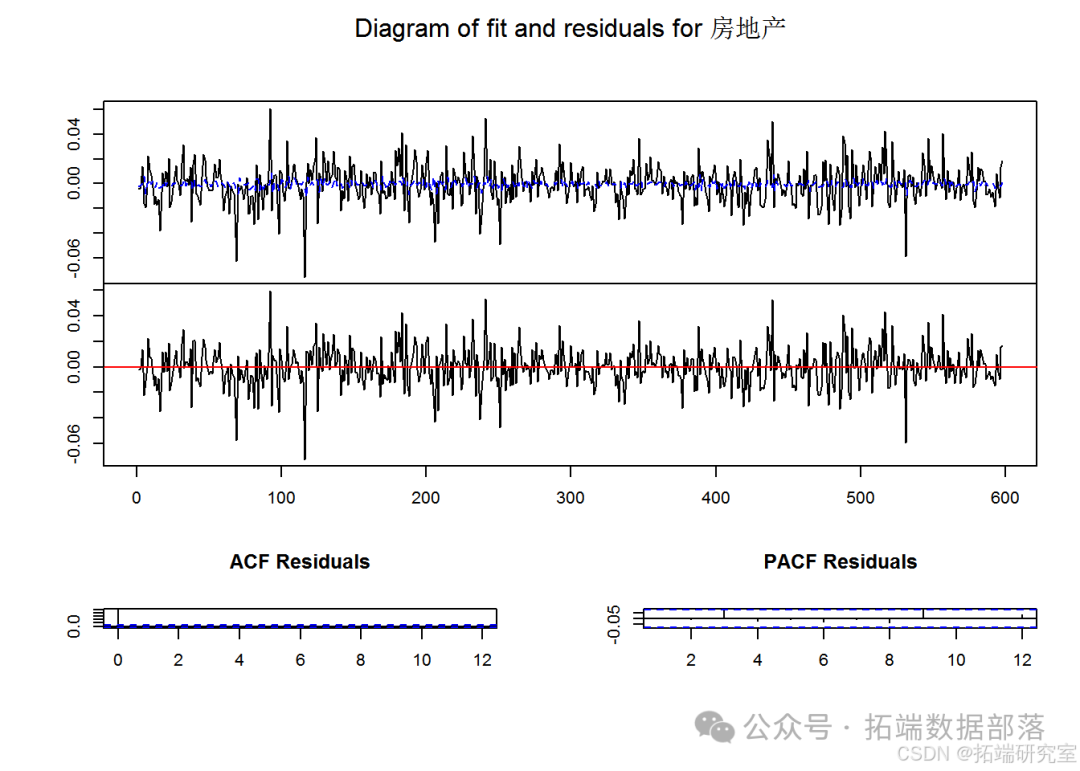
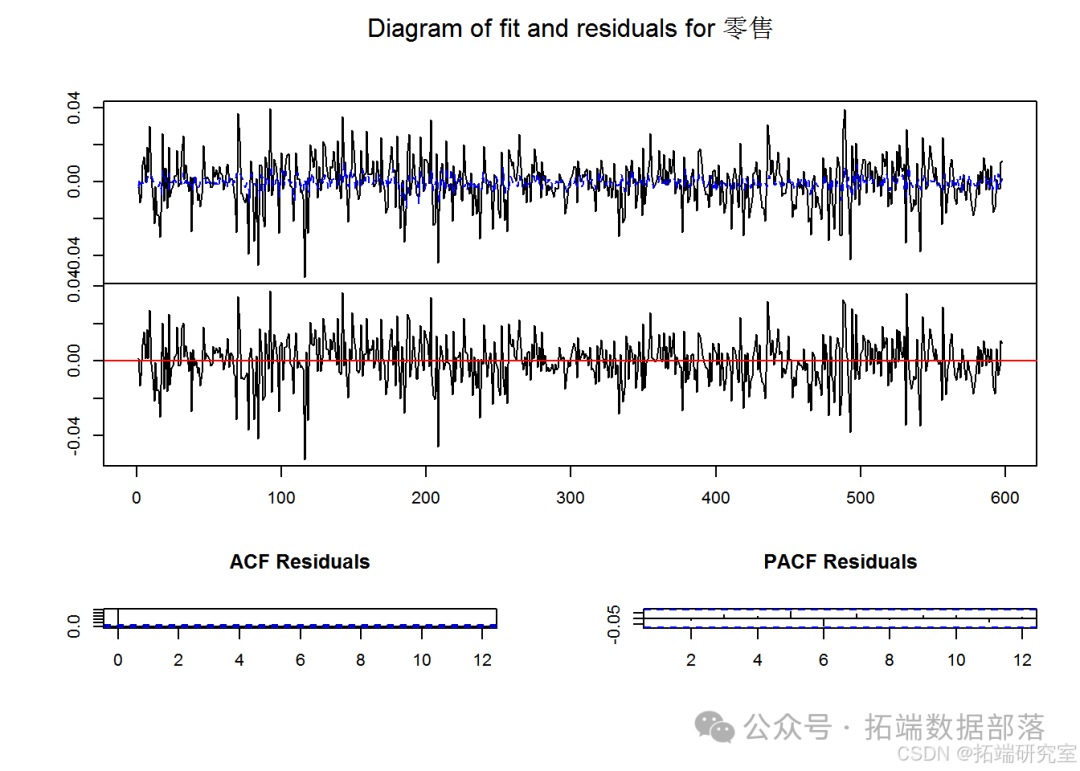
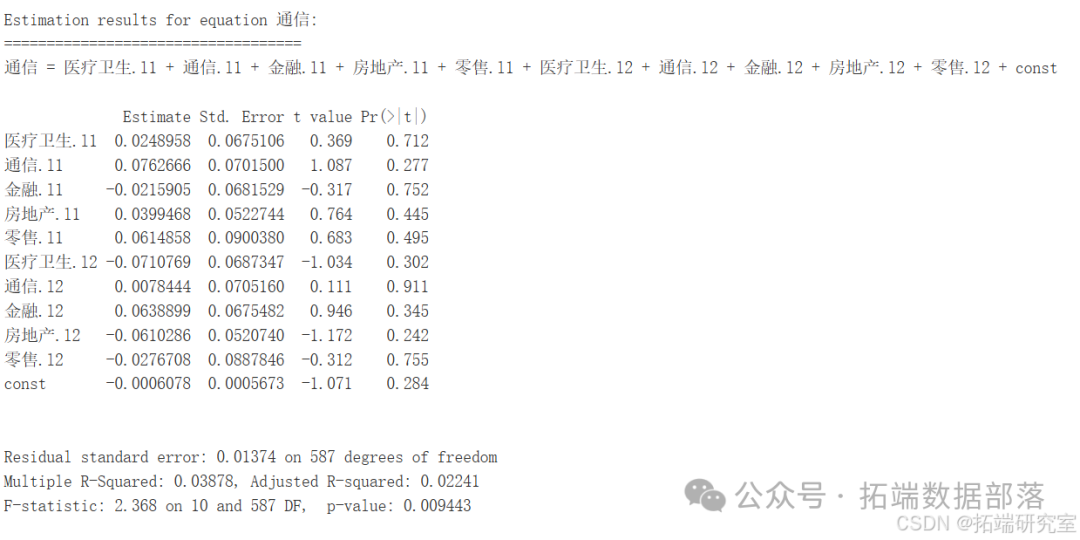
VAR 模型估计结果
对各个行业方程的估计系数、标准误差、t 值和 p 值进行了详细呈现和分析。
医疗卫生行业
部分变量呈现出显著影响,这表明在医疗卫生领域,某些因素对其发展和变化具有明确且重要的推动或抑制作用。通信行业
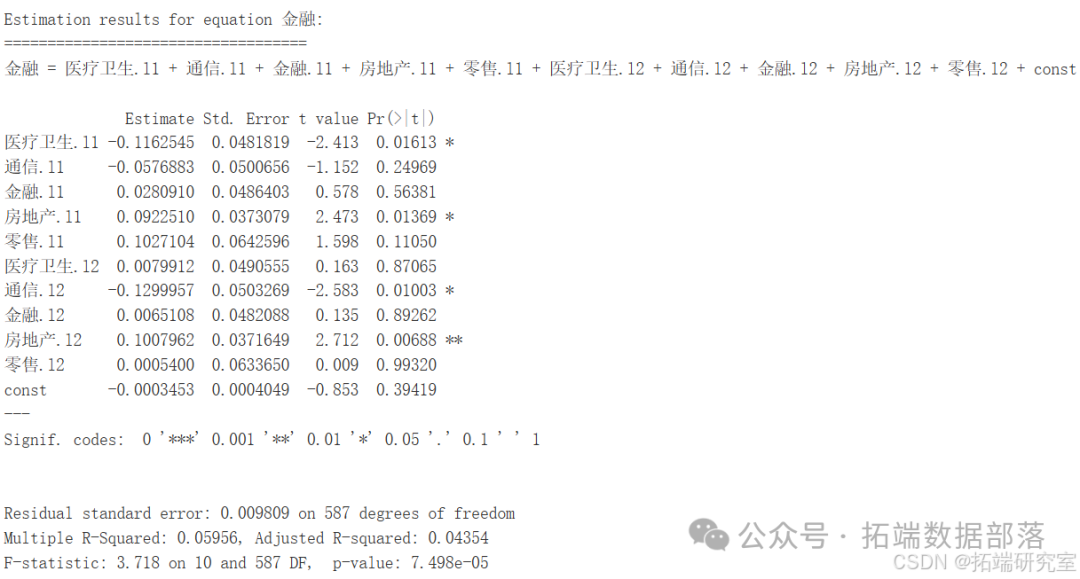
部分变量的影响不显著,暗示在通信行业中,某些因素可能并非是决定其发展走向的关键因素。金融行业
部分变量具有显著作用,反映出金融行业的发展受到特定因素的显著驱动。房地产行业
部分变量的显著性得以体现,揭示了在房地产行业中存在对其发展具有重要影响的特定因素。零售行业
一些变量具有显著影响,意味着在零售行业的发展过程中,存在着能够显著左右其发展态势的关键因素。给出了残差的标准误差、多重 R 平方、调整后的 R 平方以及 F 统计量和相应的 p 值。
点击标题查阅往期内容
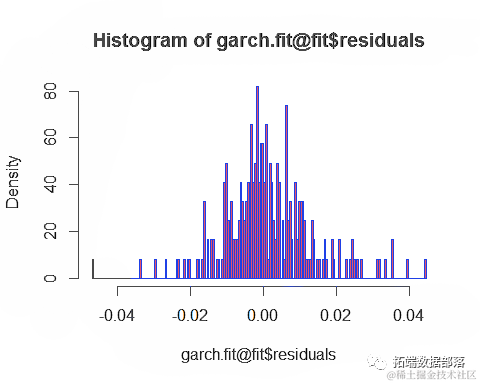
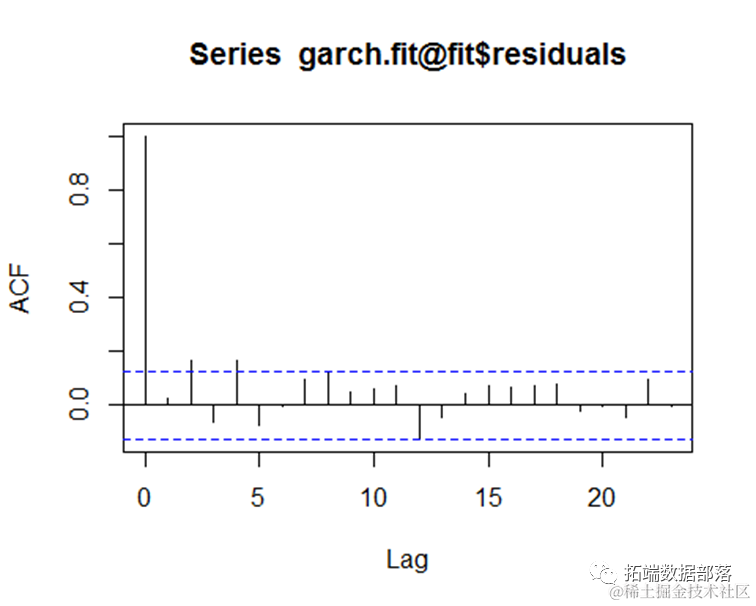
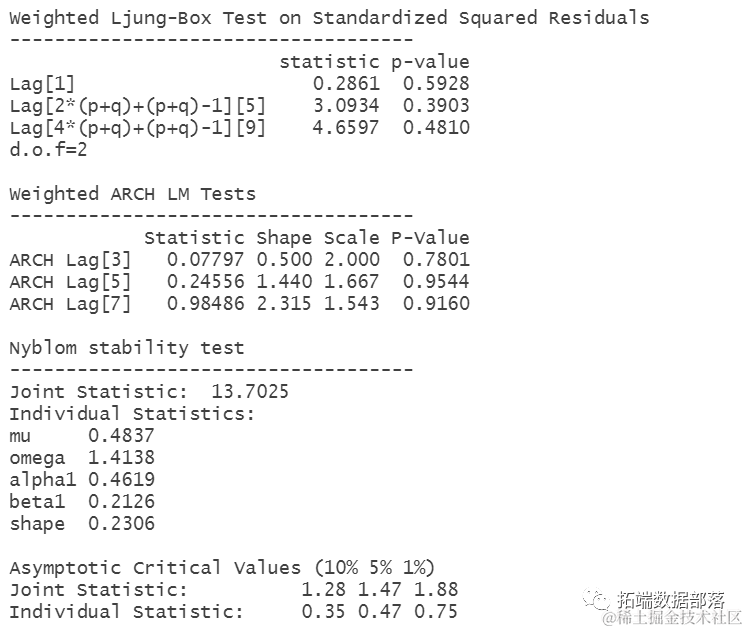
R语言软件套保期限GARCH、VAR、OLS回归模型对沪深300金融数据可视化分析

左右滑动查看更多

01
02
03
04
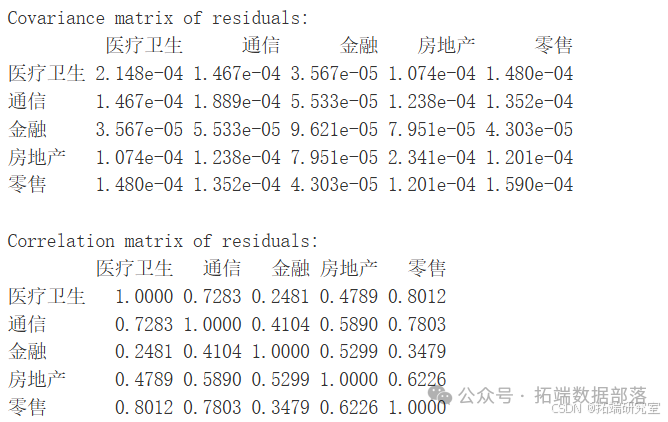
(二)残差的协方差和相关矩阵
展示了各行业残差之间的协方差和相关关系。
然后使用该估计值计算连通性度量
首先,计算如迪博尔德和伊尔马兹所述的不依赖频率的传统总体度量,并且具有将互相关元素置零的可能性。这些命令会打印出表格和所有相关度量。
计算传统溢出效应
spilloverDY09(est, n.ahead = 100, no.corr = F) 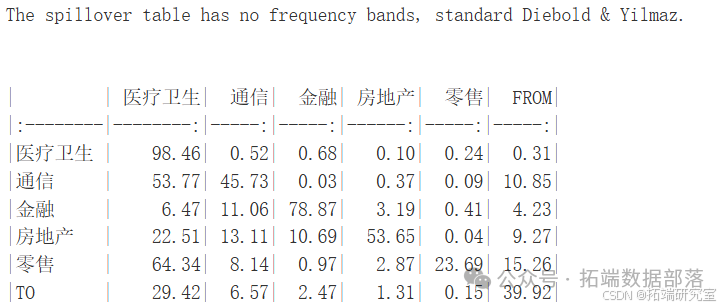
遵循的是标准的 Diebold & Yilmaz 方法。
从各行数据来看:
医疗卫生行业自身的溢出效应(即对自身的影响)达到 98.46,说明该行业的变化主要受自身因素影响,对其他行业的溢出相对较小。
通信行业对自身的溢出效应为 45.73,同时对医疗卫生行业有 0.52 的溢出,对金融行业的溢出仅为 0.03 等,表明通信行业与医疗卫生行业有一定的关联,与金融行业的关联较弱。
金融行业自身的溢出效应为 78.87,对其他行业的溢出相对较小。
房地产行业自身的溢出效应为 53.65,对医疗卫生行业的溢出为 0.10 等。
零售行业对自身的溢出效应为 23.69。
溢出效应分析
计算传统的溢出效应,给出了各行业之间的溢出和接收的具体数值。
通过滚动估计分析溢出效应的动态变化,并进行可视化展示。
利用这些,可以绘制所得的溢出度量。
plotOverall(sp)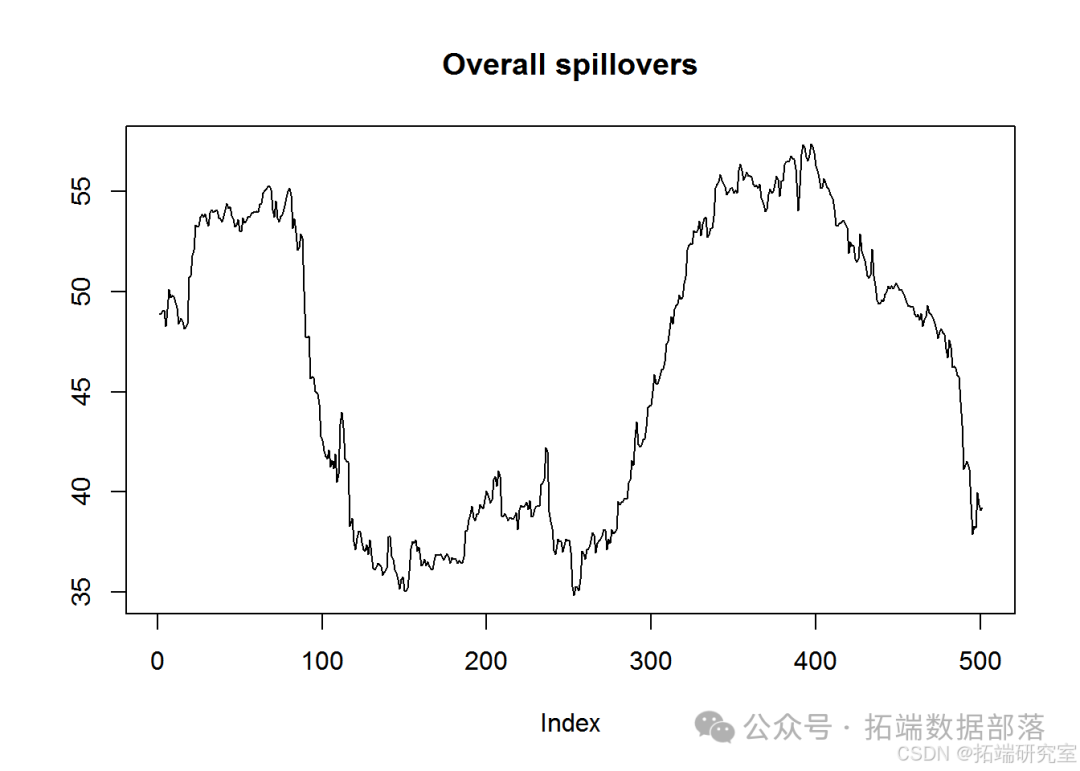
plotTo(sp)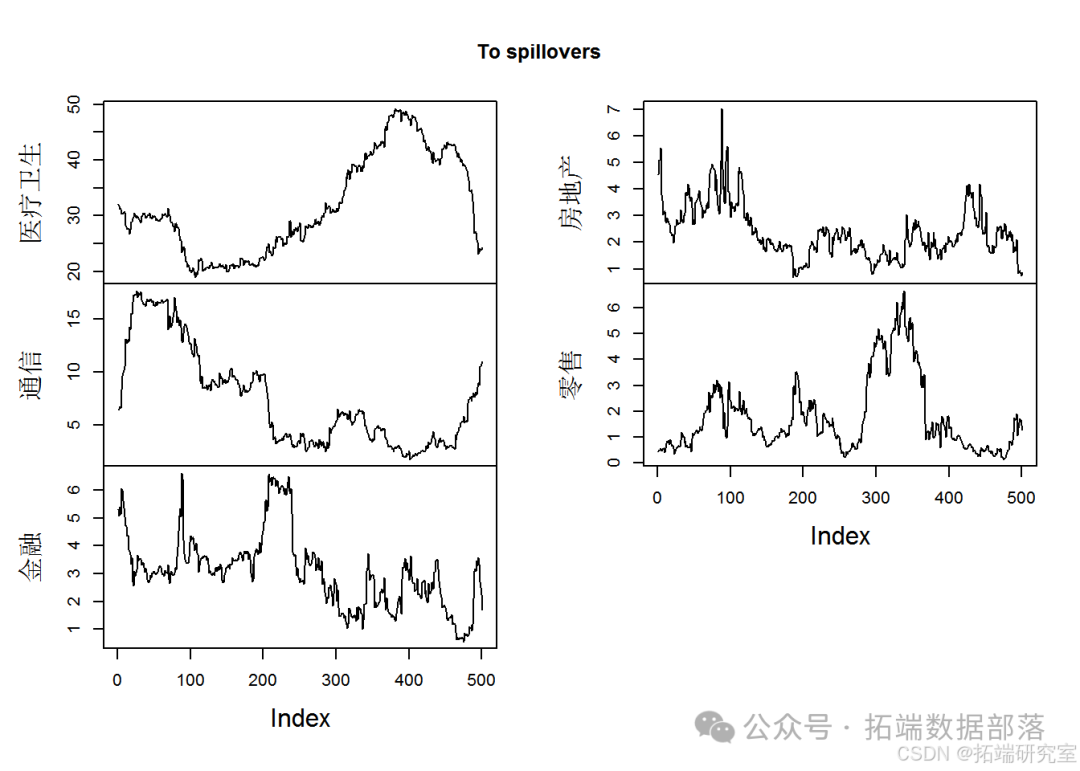
plotFrom(sp)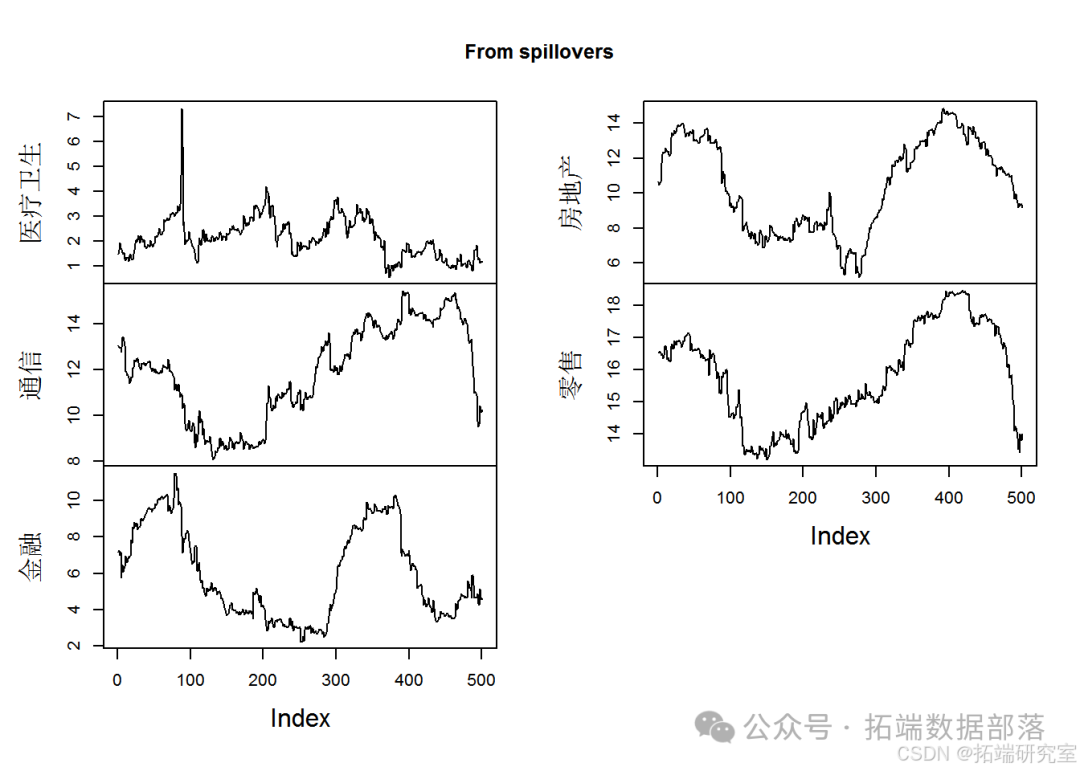
plotNet(sp)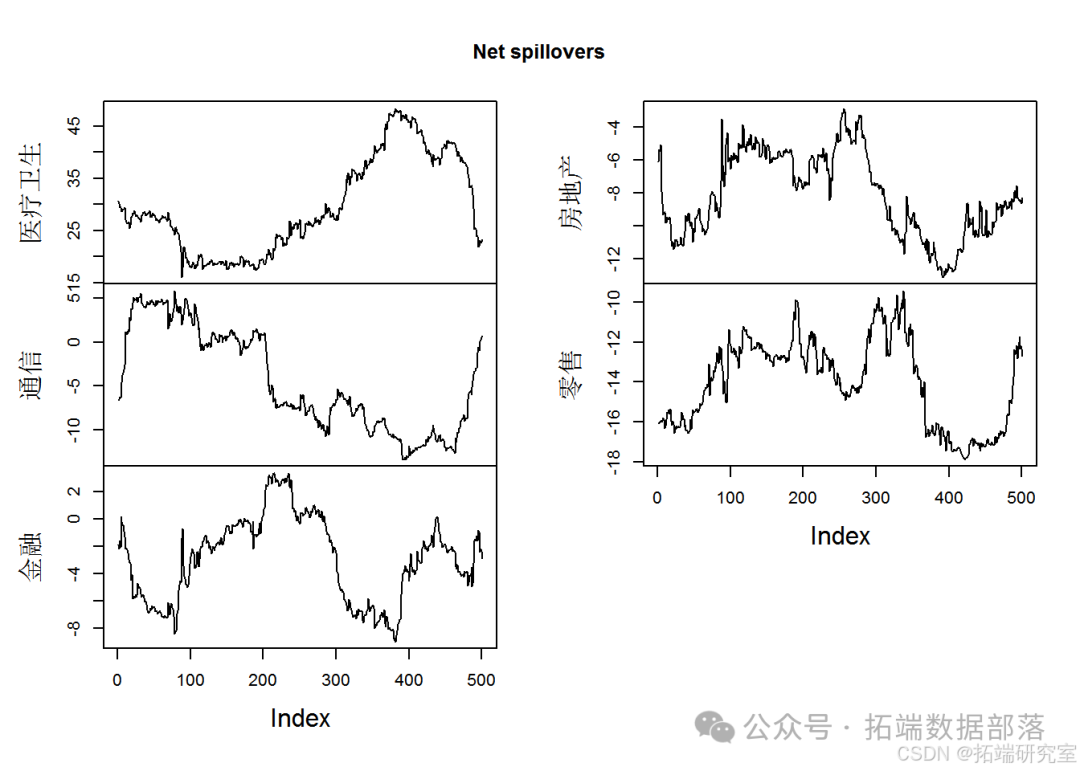
plotPairwise(sp)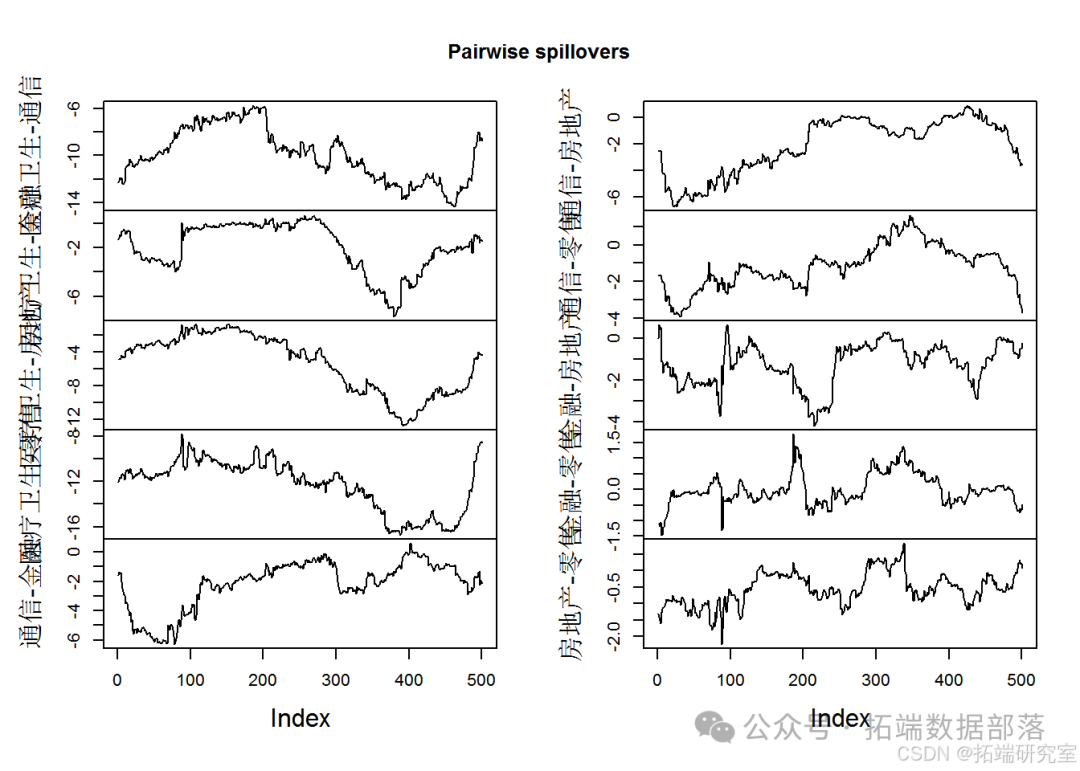
上述代码实现了数据的读取、收益率的计算、VAR (2) 估计值的计算与保存,接着基于估计值进行连通性度量的计算,包括传统溢出效应等,并通过一系列绘图函数展示相关结果。通过这样的处理和分析,能够深入研究数据中的内在关系和特征。

本文中分析的数据、代码分享到会员群,扫描下面二维码即可加群!
资料获取
在公众号后台回复“领资料”,可免费获取数据分析、机器学习、深度学习等学习资料。

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言VAR模型的多行业关联与溢出效应可视化分析》。
点击标题查阅往期内容
Garch波动率预测的区制转移交易策略
金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言风险价值:ARIMA,GARCH,Delta-normal法滚动估计VaR(Value at Risk)和回测分析股票数据
R语言GARCH建模常用软件包比较、拟合标准普尔SP 500指数波动率时间序列和预测可视化
Python金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测
R语言GARCH-DCC模型和DCC(MVT)建模估计
Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
R语言时间序列GARCH模型分析股市波动率
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测
使用R语言对S&P500股票指数进行ARIMA + GARCH交易策略
R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模
R语言股票市场指数:ARMA-GARCH模型和对数收益率数据探索性分析
R语言多元Copula GARCH 模型时间序列预测
R语言使用多元AR-GARCH模型衡量市场风险
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格
R语言用Garch模型和回归模型对股票价格分析
GARCH(1,1),MA以及历史模拟法的VaR比较
matlab估计arma garch 条件均值和方差模型
R语言POT超阈值模型和极值理论EVT分析
R语言极值推断:广义帕累托分布GPD使用极大似然估计、轮廓似然估计、Delta法
R语言极值理论EVT:基于GPD模型的火灾损失分布分析
R语言有极值(EVT)依赖结构的马尔可夫链(MC)对洪水极值分析
R语言POT超阈值模型和极值理论EVT分析
R语言混合正态分布极大似然估计和EM算法
R语言多项式线性模型:最大似然估计二次曲线
R语言Wald检验 vs 似然比检验
R语言GARCH-DCC模型和DCC(MVT)建模估计
R语言非参数方法:使用核回归平滑估计和K-NN(K近邻算法)分类预测心脏病数据
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
R语言基于Bootstrap的线性回归预测置信区间估计方法
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型
Matlab马尔可夫区制转换动态回归模型估计GDP增长率
R语言极值推断:广义帕累托分布GPD使用极大似然估计、轮廓似然估计、Delta法



![]()