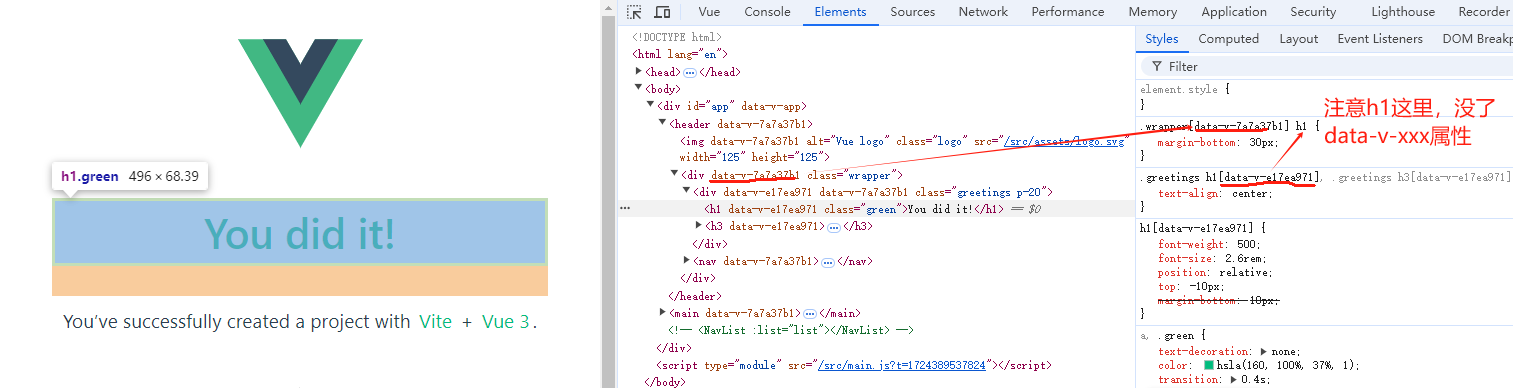
题目：

题解：

class Solution {
    public boolean isPerfectSquare(int num) {
        double x0 = num;
        while (true) {
            double x1 = (x0 + num / x0) / 2;
            if (x0 - x1 < 1e-6) {
                break;
            }
            x0 = x1;
        }
        int x = (int) x0;
        return x * x == num;
    }
}