软考：软件设计师 — 15.数据结构及算法应用

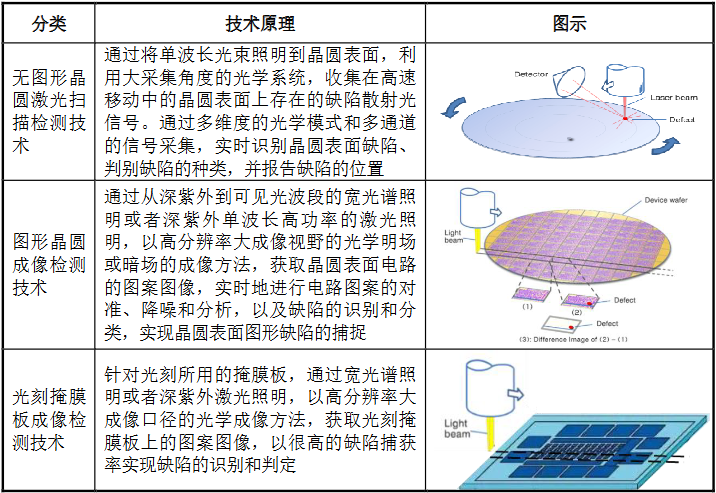
十五. 数据结构及算法应用

数据结构及算法应用类题目是下午场考试中的第四道题目，分值 15 分，主要以 C 语言填空、算法策略判断和时间复杂度判断为考察形式，建议拿到 6 分以上。

1. 解题技巧

算法策略与时间复杂度部分详细内容可以参考文章：软考：软件设计师 — 14.算法基础

（1）算法策略区分

分治法（主要是二分）

特征：把一个问题拆分成多个小规模的相同子问题，一般可用递归解决。

经典问题：斐波那契数列、归并排序、快速排序、二分搜索、矩阵乘法、大整数乘法等

贪心法（一般用于求满意解）

特征：局部最优，但整体不见得最优。每步有明确的、既定的策略。

经典问题：背包问题（如装箱）、多机调度、找零钱问题

动态规划法（用于求最优解）

特征：划分子问题，并把子问题结果适用数组存储，利用查询子问题结果构造最终问题结果。（一般自顶向下时间复杂度为 O( $2^{n}$ )，自底向上时间复杂度为 O( $n^{a}$ )，后者效率更高）

经典问题：斐波那契数列、矩阵乘法、背包问题、LCS最长公共子序列

回溯法

特征：系统搜索一个问题的所有解或任一解。

经典问题：N皇后问题、迷宫、背包问题

算法名称	关键点	特征	典型问题
分治法	递归技术	把一个问题拆分成多个小规模的相同子问题，一般可用递归解决。	归并排序、快速排序、二分搜索
贪心法	一般用于求满意解，特殊情况可求最优解（部分背包）	局部最优，但整体不一定最优。每步有明确的、既定的策略。	背包问题（如装箱）、多机调度、找零钱问题
动态规划法	最优子结构和递归式	划分子问题（最优子结构），并把子问题结果使用数组存储，利用查询子问题结果构造最终问题结果。	矩阵乘法、背包问题、LCS最长公共子序列
回溯法	探索和回退	系统搜索一个问题的所有解或任一解。有试探和回退的过程。	N皇后问题、迷宫、背包问题

算法策略判断：

回溯：有尝试探索和回退的过程。
分治：分治和动态规划比较难区分。分治不好解决问题，从而记录中间解解决问题。分治主要采用二分的思想，二分以外都用动态规划法解决了。二分的时间复杂度与 O(nlog2n) 相关，需注意有无外层嵌套循环，如果有，则需要再乘 n。（结合归并排序、快速排序的过程，也是二分的）
动态规划法：有递归式，自底向上实现时，中间解基本上查表可得，时间复杂度一般是 O( $n^{a}$ )，具体 a 的值取决于 for 循环的嵌套层数。如果循环变量从 0 或 1 开始，到 n 结束，这种情况就是从小规模到大规模，自底向上。如果自顶向下，时间复杂度为 O( $2^{n}$ )，和分治的实现就差不多了，查表的意义可以忽略不记，循环变量一般由 n 开始，向 1 缩小，是从大规模到小规模。
贪心法：有时也会出现最优子结构的描述，但没有递归式。考虑的是当前最优，求得的是满意解。

（2）时间复杂度与空间复杂度

常见的对算法执行所需时间的度量：

O(1)<O( $log_{2}n$ )<O(n)<O( $nlog_{2}n$ )<O( $n^{2}$ )<O( $n^{3}$ )<O( $2^{n}$ )

（3）代码填空技巧

仔细审题：

检查所有用到的变量是否有声明，是否赋初值；
检查是否有返回值，与题干要求返回变量名或上下文是否一致；
检查 for 循环是否有计数变量的赋值、初值和终止条件；
注意 while 循环的开始和结束；
有一些变量名具有特殊含义，比如一般用 max/min 保存最大值/最小值，temp 作为中间变量，一般用来存储中间值或用来做数值交换的中间过渡。x>max，则修正 max=x；x<min，则修正 min=x；
对特殊的算法策略：回溯法是否有回退 k=k-1；分治法递归的递归调用（调用自身函数名）；动态规划法的查表操作；
注意题干描述和代码说明、递归式（条件和等式）、代码中的注释、代码上下文。一般特殊数据结构调用方式会在代码说明或代码上下文中给出。

题干公式很重要，一般公式体现在代码中，会有循环边界、判断条件等；
代码说明很重要，一般代码说明会指出一些变量的定义、初始值和边界值；
代码上下文很重要，可以根据上下文判断有没有缺失变量声明、变量赋值；
题干说明很重要，题干有时候会给出循环边界、判断条件等内容。还可以根据题干描述，判断使用的算法策略，不同的算法策略，一般会有一些典型的代码缺失，比如：动态规划法可能会考察题干给出的递归式以及最优解的判断；分治法一般会考察递归式以及问题的划分；贪心法一般会考察满意解的当前最优判断条件；回溯法一般会考察回退的过程。

2. 例题

（1）背包问题介绍

有 n 物品，第 i 个物品价值为 $v_{i}$ ，重量为 $w_{i}$ ，其中 $v_{i}$ 和 $w_{i}$ 均为非负数，背包的容量为 W，W 为非负数。现需要考虑如何选择装入背包的物品，使装入背包的物品总价值最大。

部分背包问题（物品可分割）

这类问题通常可以通过依次选择单位价值（ $v_{i}$ / $w_{i}$ ）最大的物品进行放入，剩余体积不够时，进行切割，从而得到最优结果。

0-1 背包问题（物品不可分割）

形式化描述如下：

目标函数为 $max\sum_{i=1}^{n}v_{i}x_{i}$

约束条件为 $\sum_{i=1}^{n}w_{i}x_{i}\leq W,x_{i}\in {0,1}$

满足约束条件的任一集合 $(x_{1},x_{2},\cdots ,x_{n})$ 是问题的一个可行解。

放置策略

可以将背包问题的求解过程看作是进行一系列决策的过程，即决定哪些物品应该放入背包，哪些物品不放入背包。

优先放体积最大，超过背包体积则放弃其它物品（5，4；30）；
优先放价值最大，超过背包体积则放弃其它物品（5，4；30）；
优先放单位价值最大，超过背包体积则放弃其它物品（5，3；29）；
按顺序放置，不合适就退出来重新放置，直到尝试完背包能够放置的所有方案；
刻画 0-1 背包问题的最优解的结构：

如果一个问题的最优解包含了物品 n，即 $x_{n}=1$ ，那么其余 $x_{1},x_{2},\cdots ,x_{n-1}$ 一定构成子问题 1，2，…，n-1 在容量 $W-w_{n}$ 的最优解。如果这个最优解不包含物品 n，即 $x_{n}=0$ ，那么其余 $x_{1},x_{2},\cdots ,x_{n-1}$ 一定构成子问题 1，2，…，n-1 在容量 W 的最优解。

如果题目中有对最优子结构的描述，用贪心法可以求得最优解（参考贪心法求解部分背包问题）。

（2）背包问题 - 贪心法

说明：

设有 n 个货物要装入若干个容量为 C 的集装箱以便运输，这 n 个货物的体积分别为 { $S_{1},S_{2},\cdots ,S_{n}$ }，且有 $S_{i}$ ≤ C（1≤i≤n）。为节省运输成本，用尽可能少的集装箱来装运这 n 个货物。

下面分别采用最先适宜策略和最优适宜策略来求解该问题。

最先适宜策略首先将所有的集装箱初始化为空，对于所有货物，按照所给的次序，每次将一个货物装入第一个能容纳它的集装箱中。

最优适宜策略与最先适宜策略类似，不同的是，总是把货物装到能容纳它且目前剩余容量最小的集装箱，使得该箱子装入货物后闲置空间最小。

C代码：

变量说明

n：货物数

C：集装箱容量

s：数组，长度为 n，其中每个元素表示货物的体积，下标从 0 开始

b：数组，长度为 m，b[i] 表示第 i+1 个集装箱当前已经装入货物的体积，下标从 0 开始

i，j：循环变量

k：当前所用的集装箱数量

min：集装箱装入了第 i 个货物后的最小剩余容量

m：当前所需要的集装箱数量

temp：临时变量

具体代码

（1）最先适宜策略

/* 最先适宜策略首先将所有的集装箱初始化为空，对于所有货物，
按照所给的次序，每次将一个货物装入第一个能容纳它的集装箱中 */

int firstfit(){
  int i,j;
  k=0;
  for(i=0; i<n; i++){
   b[i]=0;
  }
  for(i=0; i<n; i++){
  (1);
   while(C-b[i]<s[i]){
    j++;
   }
  (2);
  k=k>(j+1)?k:(j+1);
  }
  return k;
}

（2）最优适宜策略

/* 最优适宜策略与最先适宜策略类型，不同的是，
总是把货物装到能容纳它且目前剩余容量最小的集装箱中，使得该箱子装入货物后闲置空间最小。*/

int bestfit(){
  int i,j,min,m,temp;
  k=0;
  for(i=0; i<n; i++){
  b[i]=0;
  }
  for(i=0; i<n; i++){
   min=C;
   m=k+1;
   for(j=0; j<k+1; j++){
     temp=C-b[i]-s[i];
     if(temp>0&&temp<min){
       (3);
       m=j;
     }
   }
   (4);
   k=k>(m+1)?k:(m+1);
  }
  return k;
}

问题1：

根据说明和 C 代码，填充 C 代码中的空（1）~（4）；

问题2：

根据说明和 C 代码，该问题在最先适宜和最优适宜策略下分别采用了（5）和（6）算法设计策略，时间复杂度分别为（7）和（8）。

问题3：

考虑实例 n=10，C=10，各个货物的体积为 {4，2，7，3，5，4，2，3，6，2}。该实例在最先适宜和最优适宜策略下所需的集装箱数分别为（9）和（10）。考虑一般的情况，这两种求解策略能否确保得到最优解？（11）（能或否）

解析1：

在最先适宜策略代码中，第一个 for 循环中首先初始化了每个集装箱中装入货物的体积，第二个 for 循环中，有 while 循环去判断剩余集装箱的体积与每个货物的体积情况，货物体积大于集装箱剩余体积，则 j++，进入下一个集装箱。每个变量使用前都需要初始化，变量 j 没有初始化，因此第（1）空处填写初始化 j 变量的操作，即 j=0。如果货物体积不大于集装箱剩余体积，那么就说明可以放入集装箱中，因此第（2）处缺失的是装箱的操作，即 b[i] = b[i] + s[i]。

在最优适宜策略代码中，第一个 for 循环中首先初始化了每个集装箱中装入货物的体积，第二个 for 循环中，首先将集装箱容量初始化为最小，因为一开始集装箱中没装任何货物，也是最小剩余容量，m 代表当前所需要的集装箱数量或者集装箱的编号，因为初始编号从 0 开始，嵌套的 for 循环去遍历目前用到的集装箱，因为货物要放入能容纳它并且目前集装箱容量最小的那个，使用 temp 存储目前各集装箱的剩余容量，如果 temp 大于 0 （合法）并且比当前最小值要小的话，说明此时的最小值应该是 temp，找到当前剩余容量最小的集装箱，同时把遍历的第几个集装箱赋值给 m，那么此时的最小值是temp，即 min = temp；下一步缺少的也是装箱操作，注意此时不再是 b[j]，而是 b[m]，b[m] 才是目前剩余容量最小的集装箱，即 b[m] = b[m] + s[i]。

（1）j=0 （2）b[j] = b[j] + s[i]（3）min = temp （4）b[m] = b[m] + s[i]

解析2：

最先适宜策略是将货物装到第一个能容纳它的集装箱中，考虑的是局部最优，即贪心策略；最优适宜策略虽然有最优的概念，但是将货物装入能容纳它且目前剩余容量最小的箱子中，考虑的也是局部最优，即贪心策略。根据它们的 C 代码，最先适宜策略中涉及到两个平行的 for 循环以及一个嵌套进第二个 for 循环的 while 循环，有两层遍历，一层是遍历货物 n，一层是判断货物的体积与集装箱剩余的体积，因此时间复杂度为 O( $n^{2}$ )；最优适宜策略中涉及到了两层嵌套的 for 循环，一层是遍历货物，一层是遍历集装箱，因此时间复杂度为 O( $n^{2}$ )。

（5）贪心（6）贪心（7）O( $n^{2}$ ) （8）O( $n^{2}$ )

解析3：

具体实例的判断可通过画图或者推理得出，最先适宜策略是放入第一个能容纳当前货物的集装箱中，最优适宜策略是放入能容纳当前货物且目前剩余容量最小的集装箱中：