题目链接: https://leetcode.cn/problems/counting-bits/
视频题解: https://www.bilibili.com/video/BV1RE421w7C7/
LeetCode 338. 比特位计数
题目描述
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
举个例子:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
知识回顾
动态规划是一种通过将原问题分解为子问题来求解复杂问题的算法思想。它通常用于求解最优化问题,例如最长公共子序列、背包问题等。动态规划的核心思想是将原问题分解为若干个子问题,通过求解子问题的最优解自下而上推导出原问题的最优解。
视频题解
比特位计数
思路来源
思路来源
思路解析
如果对区间[0, n]上的数逐个求对应二进制中1的个数是比较耗时的,下面来介绍使用动态规划来解此题。动态规划的关键是推导状态转移公式和边界条件处理。
下面介绍这道题目两种不同状态转移公式。
方法一
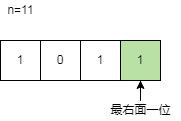
首先复习一下二进制的基本操作,如何获取n对应二进制的最右边一位和怎样将n对应的二进制向右移一位。
获取n对应二进制最右面一位有两种方式:
n和1进行与运算n & 1可以获取n对应二进制的最右面一位。n对2取余n % 2即可获取n对应二进制的最右面一位。
将n对应的二进制右移一位有两种方式:
- 直接使用编程语言自带的右移符号,比如
c++可以写为n >> 1。 n / 2也可以将n对应的二进制右移一位。

进入正题,定义dp[i]为i的二进制中1的个数, 观察整数区间[0,4]对应的二进制。

把4对应的二进制向右移动一位,就变成了2对应的二进制,4和2的二进制中的1是相同的。
dp[4] = dp[2]
把3对应的二进制向右移动一位,就变成了1对应的二进制,3的二进制比1的二进制中1的个数多1。
dp[3] = dp[1] + 1
总结上面的规律,得到状态转移公式如下:
如果整数i为偶数,也就是i的二进制最右面的bit位为0,这个时候右移,二进制中的1并没有损失,dp[i] = dp[i/2]。
如果整数i为奇数,也就是i的二进制最右面的bit位为1,这个时候右移,二进制中的1会减少一个,dp[i] = dp[i/2] + 1。
边界条件为: dp[0] = 0。
C++代码
class Solution {
public:
vector<int> countBits(int n) {
vector<int> dp(n+1, 0);
for (int i = 1; i <=n; ++i) {
if (i % 2 == 0) {
//i为偶数
dp[i] = dp[i/2];
} else {
//i为奇数
dp[i] = dp[i/2] + 1;
}
}
return dp;
}
};
java代码
class Solution {
public int[] countBits(int n) {
int[] dp = new int[n + 1];
for (int i = 1; i <= n; ++i) {
if (i % 2 == 0) {
// i为偶数
dp[i] = dp[i / 2];
} else {
// i为奇数
dp[i] = dp[i / 2] + 1;
}
}
return dp;
}
}
python代码
class Solution:
def countBits(self, n: int) -> List[int]:
dp = [0] * (n + 1)
for i in range(1, n + 1):
if i % 2 == 0:
# i为偶数
dp[i] = dp[i // 2]
else:
# i为奇数
dp[i] = dp[i // 2] + 1
return dp
方法二
我们先介绍一个骚操作,对于一个整数n,n & (n - 1)可以将n的二进制最右边值为1的bit位置为0。

在纸上继续按照上面步骤模拟一遍,会帮助大家更好的理解。
根据上面的操作可以知道n的二进制比n&(n-1)的二进制中的1多了1个,这样就可以得到状态转移公式:
dp[n] = dp[n&(n-1)] + 1
边界条件为: dp[0] = 0。
C++代码
class Solution {
public:
vector<int> countBits(int n) {
vector<int> dp(n+1, 0);
for (int i = 1; i <=n; ++i) {
//状态转移公式
res[i] = dp[i&(i-1)] + 1;
}
return dp;
}
};
java代码
class Solution {
public int[] countBits(int n) {
int[] dp = new int[n + 1];
for (int i = 1; i <= n; ++i) {
// 状态转移公式
dp[i] = dp[i & (i - 1)] + 1;
}
return dp;
}
}
python 代码
class Solution:
def countBits(self, n: int) -> List[int]:
dp = [0] * (n + 1)
for i in range(1, n + 1):
# 状态转移公式
dp[i] = dp[i & (i - 1)] + 1
return dp
复杂度分析
时间复杂度: 两种方法都是O(n),因为只遍历一遍区间[0, n]。
空间复杂度: 两种方法都是O(n),只用到一个长度为n+1的数组dp。