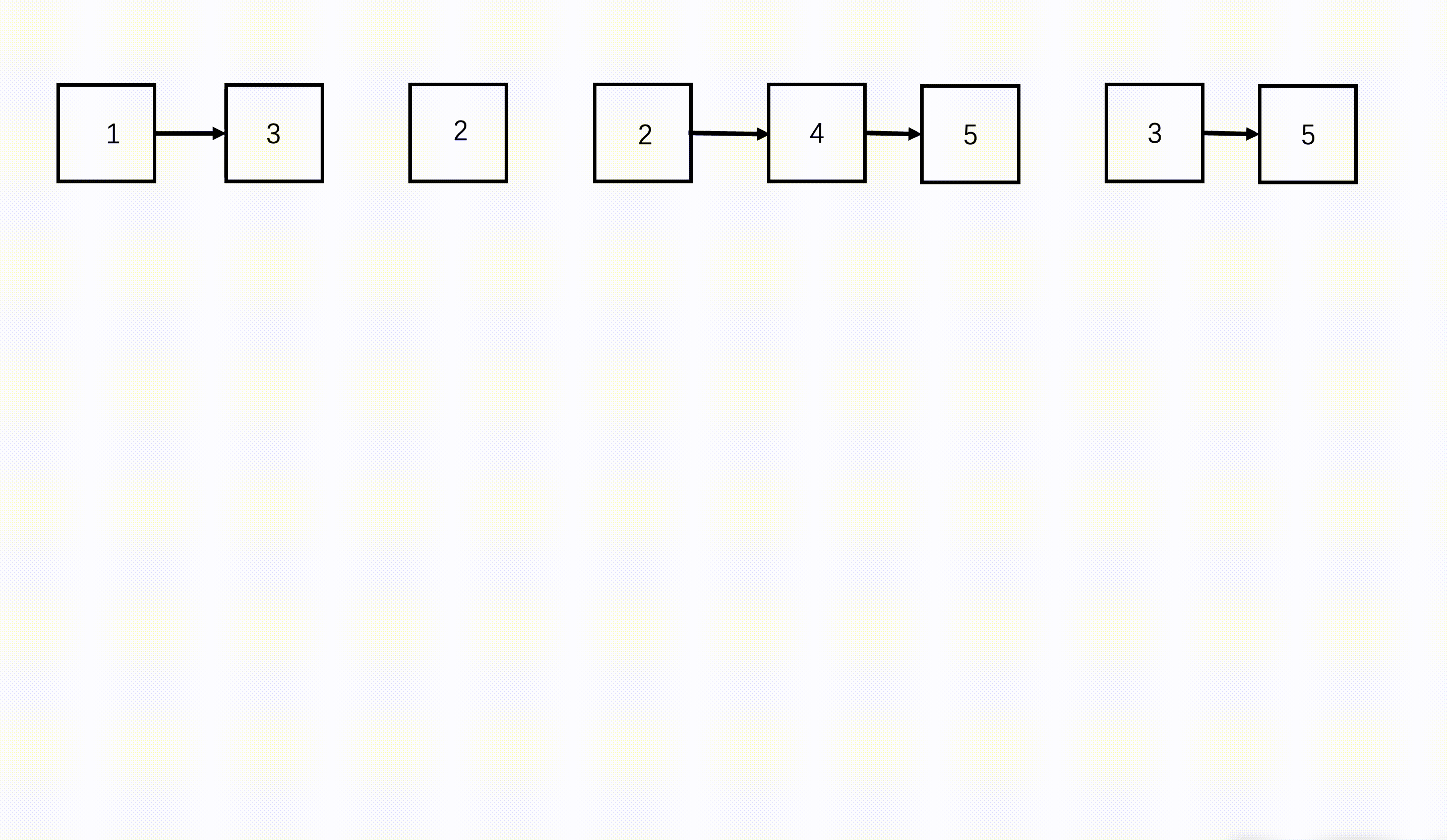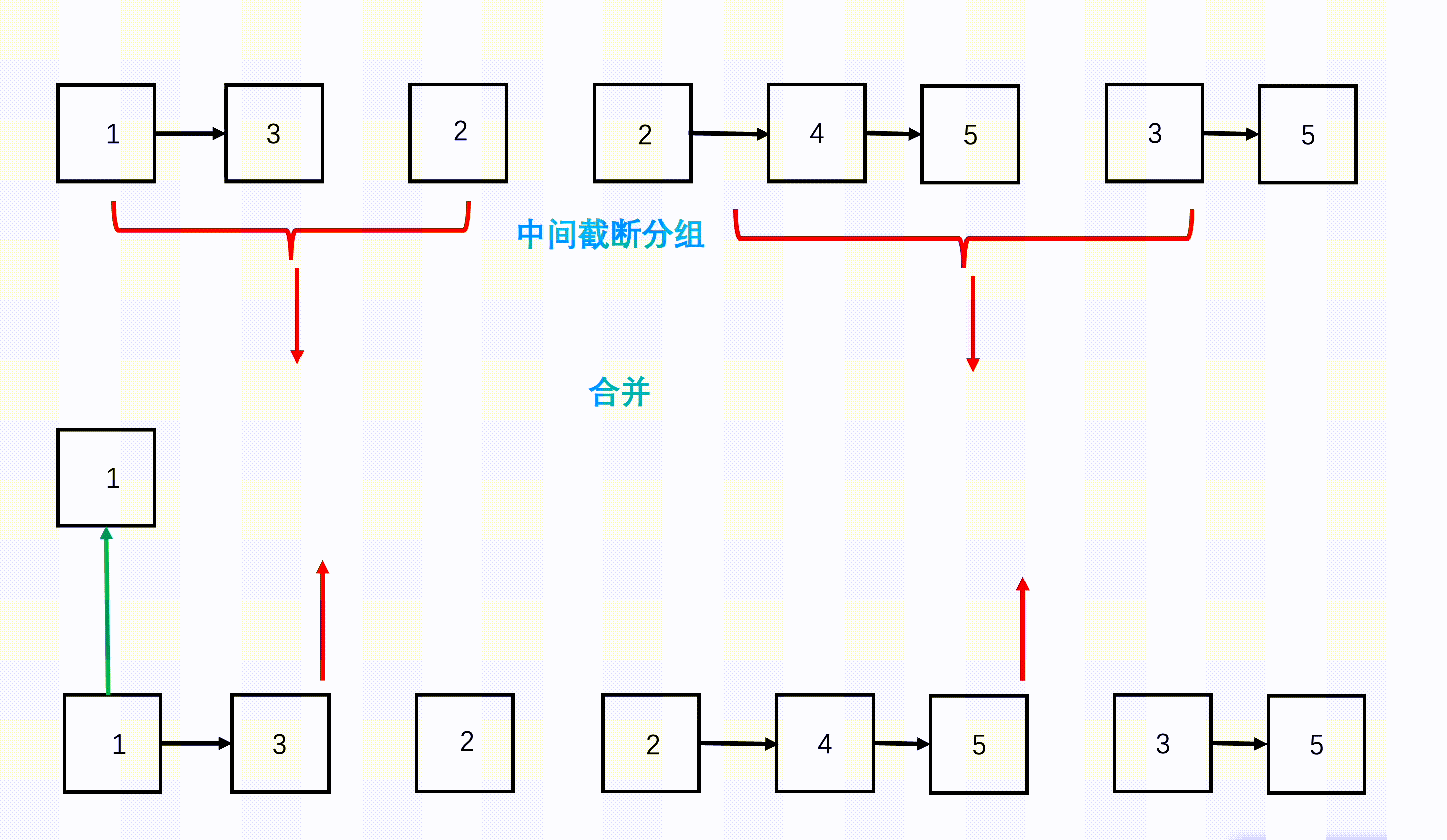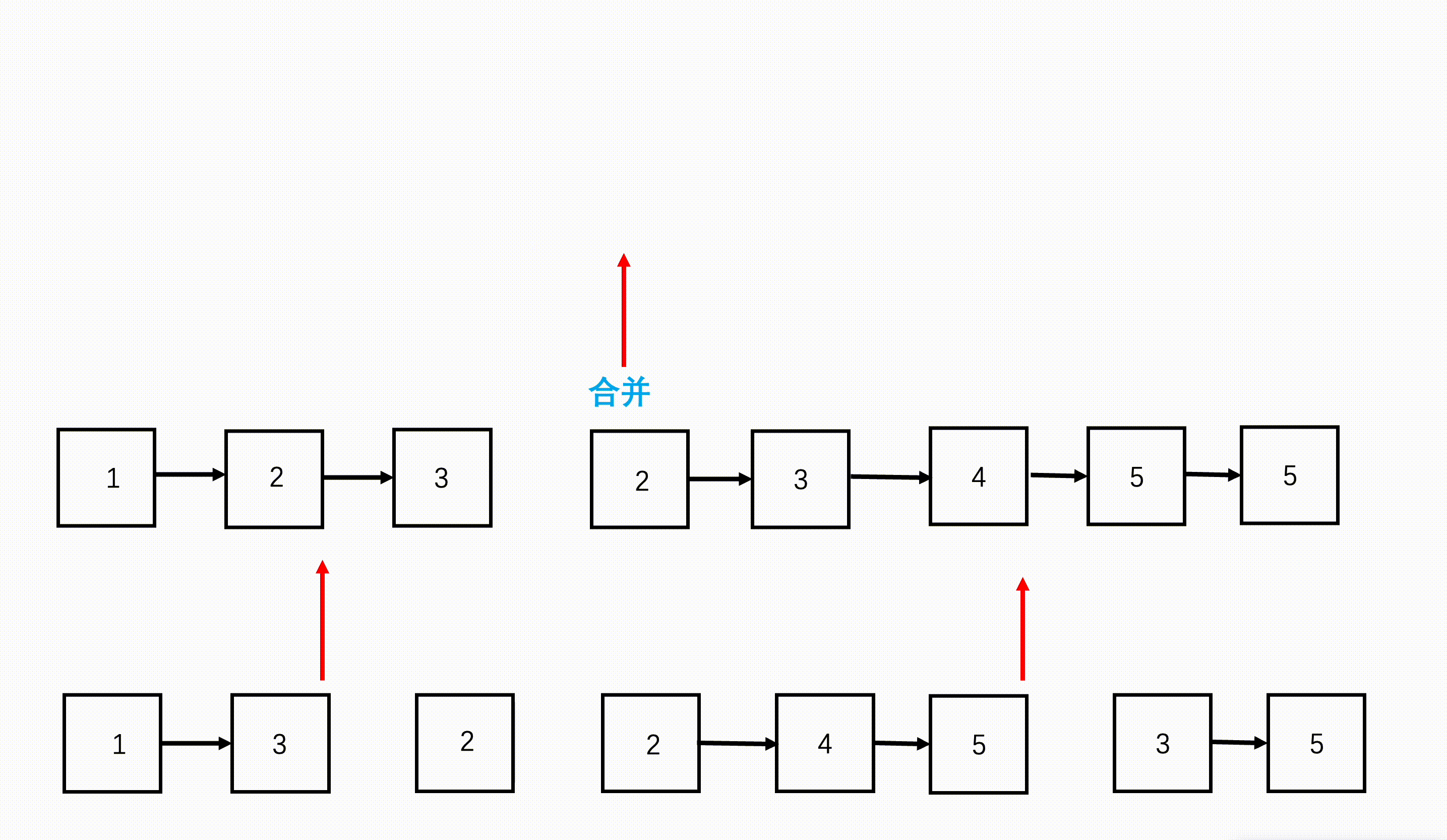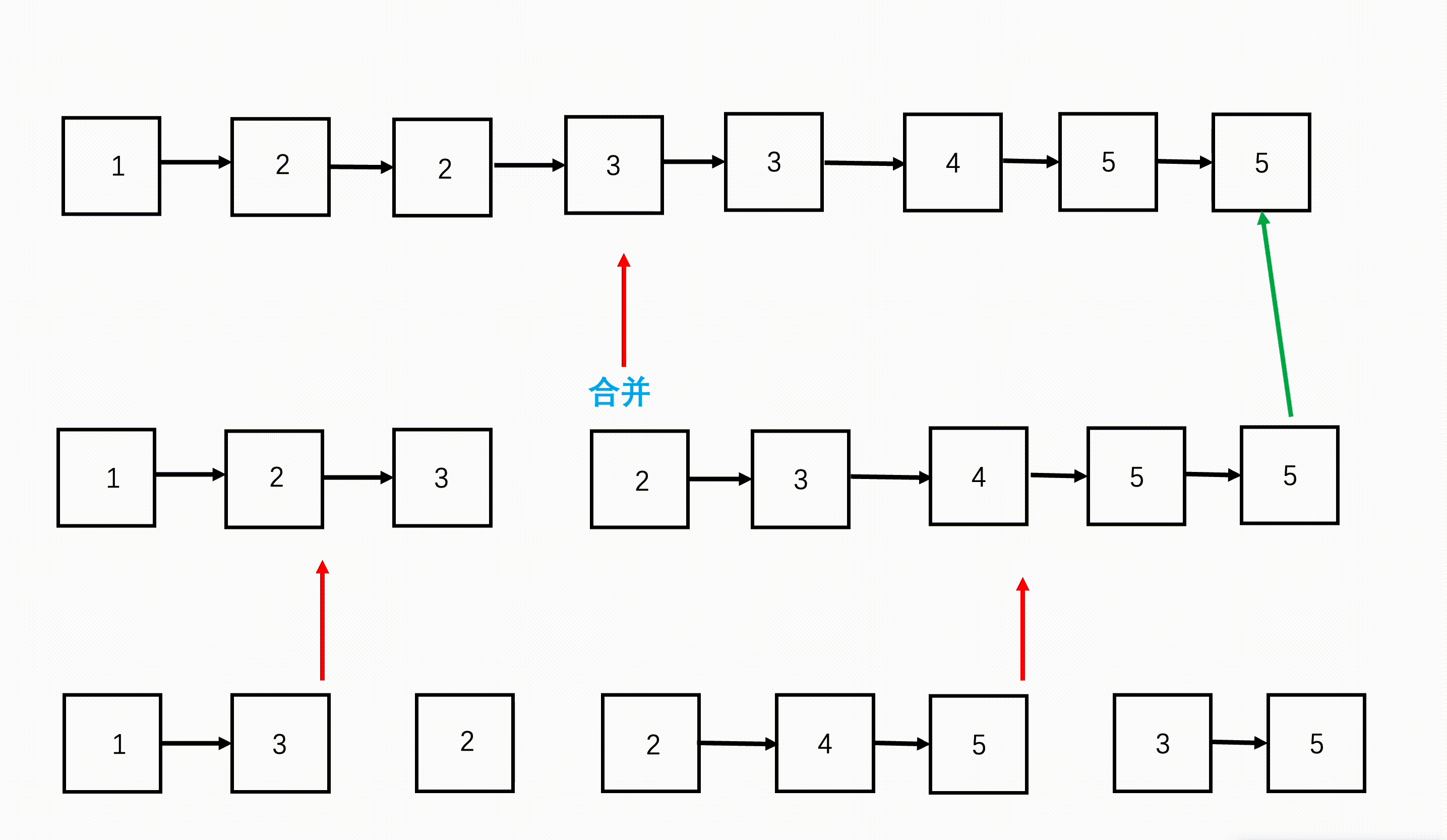目录
- 有序二叉树
- 平衡二叉树
- 构造平衡二叉树
- RR
- LL
- RL
- LR
- 平衡二叉树的优缺点:
- 2-3-4树
- 红黑树
- B树
- B+树
- B树、B+树、红黑树的应用
有序二叉树
- 关于有序二叉树的详解以及 J a v a Java Java代码实现详见:二叉排序树详解并通过Java代码实现。
- 每个节点最多有两个孩子节点。
- 任一节点的值大于其左孩子的值,小于其右孩子的值。
- 有序二叉树在查找和排序方面具有比较好的性能。
- 有序二叉树性能不稳定,查找的复杂度介于 O ( l o g n ) − O ( n ) O(logn) - O(n) O(logn)−O(n) 之间。
平衡二叉树
- 对于构造有序二叉树时出现的一些特殊的情况,例如每个节点的值都比上一个插入的值要大,那么构造出来的二叉树就会像一个链表一样向一边不断延伸。这种情况下我们对数据进行查找的复杂度就又会变成 O ( n ) O(n) O(n)。
- 为了使有序二叉树稳定,我们引入平衡二叉树,平衡二叉树在有序二叉树的基础之上,左右子树的高度差不会超过 1 1 1。这样就确保了在进行数据查找是接近 O ( l o g n ) O(logn) O(logn) 的复杂度。
- 数据在插入的过程中是无序的,为了解决这一问题,我们引入了四种算法:RR、LL、RL、LR。通过节点的旋转来使二叉树平衡。
构造平衡二叉树
RR

LL

RL

LR

平衡二叉树的优缺点:
- 优点:左右孩子节点平衡,查找消耗的时间复杂度无限接近 O ( l o g n ) O(logn) O(logn)。
- 缺点:过于复杂,构建过程会消耗计算机的性能。
2-3-4树
- 2-3-4树中存在着3种类型的节点:
| 节点名称 | 特征 |
|---|---|
| 2节点 | 存放一个数据,分出两个叉 |
| 3节点 | 存放两个数据,分出三个叉 |
| 4节点 | 存放三个数据,分出四个叉 |
- 2-3-4树的构造过程中,优先生成小节点,节点值多了存不下,就把中间的往上面挤,如果中间存放了两个数据,就把靠后的那个数据往上挤生成一个新的节点。

红黑树
- 红黑树由2-3-4 树转换而来,2节点转化为黑色节点,3节点转化为一个黑色节点下挂一个红色节点,4节点转化为一个黑色节点下挂两个红色节点。

- 红黑树的特点:
- 每个节点不是红色就是黑色。
- 根节点一定是黑色。
- 如果一个节点是红色,那个它的子节点一定是黑色。
- 从根节点到任意叶子节点上黑色节点数目是相同的。
- 最长路径(红黑交替)最多是最短路径(全黑)的两倍。
- 因此红黑树的性能介于排序二叉树和平衡二叉树之间,时间复杂度是可以接受的。
B树
- 几阶B树就表示每个节点分出几个叉。例如: M M M阶B树最多分出 M M M个叉,每个节点最多存放 M − 1 M-1 M−1个数据。
| 节点名称 | 特征 |
|---|---|
| 2节点 | 存放一个 k e y key key和 v a l u e value value,分出两个叉 |
| 3节点 | 存放两个 k e y key key和 v a l u e value value,分出三个叉 |
| 4节点 | 存放三个 k e y key key和 v a l u e value value,分出四个叉 |
| 5节点 | 存放四个 k e y key key和 v a l u e value value,分出五个叉 |
- 五阶B树构建示意图:

B+树
- B+树的非叶子节点仅具有索引作用,也就是说,非叶子节点只能存放 k e y key key 值,不存放 v a l u e value value 值,所有的 v a l u e value value 值都在叶子节点。
- 这样的存储方式能确保一页存储更多的数据,整个树的高度会更低。
- B+树的叶子节点构成一个有序链表,因此对整棵树的遍历只需要遍历叶子节点即可。
- 四阶B+树构建示意图:

B树、B+树、红黑树的应用
| 应用 | 备注 | |
|---|---|---|
| B树 | 磁盘中的数据存储 | 因为磁盘文件较多,如果用红黑树是二叉树,会导致树高度偏高,查找性能会比较差。 |
| 红黑树 | 应用于内存的数据存储 | 红黑树的查找性能接近于 O ( l o g n ) O(logn) O(logn),内存中的文件并不多,但对性能的要求较高。 |
| B+树 | 一般用于数据库中数据存储 | 因为叶子节点之间有连接,方便进行范围查找。( k e y key key 值表示主键, v a l u e value value 值表示存储数据的地址) |