目录
前言
求解方法
MATLAB验证
附:一元四次方程的故事
前言
最近在研究机器人的干涉(碰撞)检测,遇到了一个问题,就是在求椭圆到原点的最短距离时,构建的方程是一个一元四次方程。无论是高中的初等数学,大学的高等数学,还是研究生的高等代数,都没有关于一元四次方程的求解方法,大多都是一元二次方程的求解。仔细一研究才知道为什么很少提及一元四次方程。具体解法如下:
求解方法






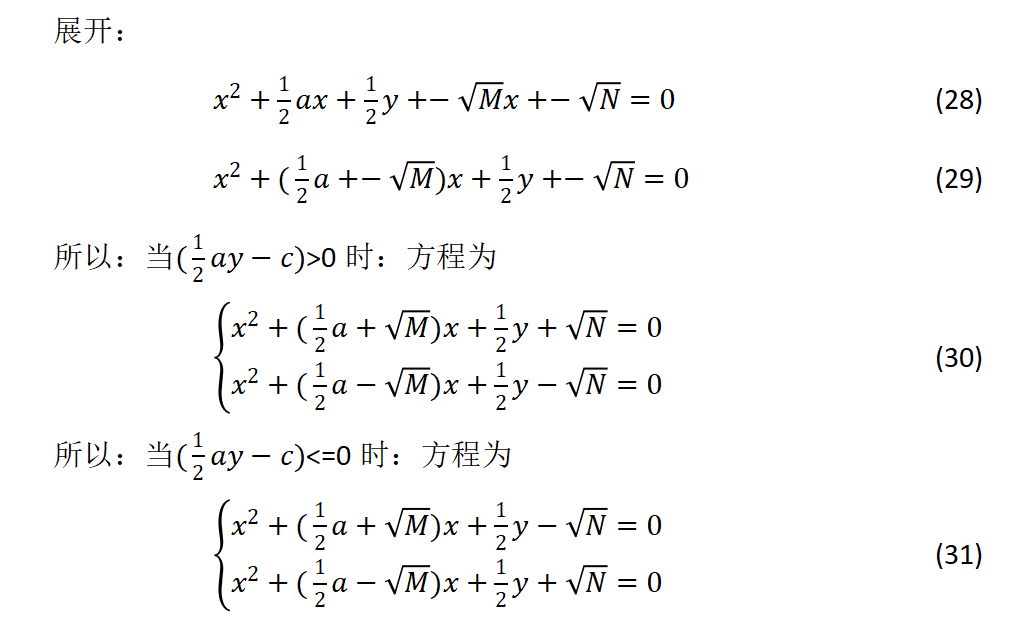

MATLAB验证
% output
% root:为方程的解(根),i 为解的个数
% input
% parameter 为方程的5个系数
function [root,i] = MYSolve4OrderEquaton(parameter)
a=parameter(2)/parameter(1);
b=parameter(3)/parameter(1);
c=parameter(4)/parameter(1);
d=parameter(5)/parameter(1);
a3=1;
b3=-b;
c3=(a*c-4*d);
d3=-(a^2*d-4*b*d+c^2);
parameter3=[a3,b3,c3,d3];
[root3,y3,i3] = Solve3OrderEquaton(parameter3);
i=0;
root=[];
for j=1:1
if(a^2/4-b+root3(j)<0||root3(j)^2/4-d<0)
break;
end
alpha=sqrt(a^2/4-b+root3(j));
beta=sqrt(root3(j)^2/4-d);
if(a*root3(j)/2-c>0)
a21=1;
b21=a/2-alpha;
c21=root3(j)/2-beta;
parameter21=[a21,b21,c21];
[root21,y21,i21] = Solve2OrderEquaton(parameter21);
a22=1;
b22=a/2+alpha;
c22=root3(j)/2+beta;
parameter22=[a22,b22,c22];
[root22,y22,i22] = Solve2OrderEquaton(parameter22);
else
a21=1;
b21=a/2-alpha;
c21=root3(j)/2+beta;
parameter21=[a21,b21,c21];
[root21,y21,i21] = Solve2OrderEquaton(parameter21);
a22=1;
b22=a/2+alpha;
c22=root3(j)/2-beta;
parameter22=[a22,b22,c22];
[root22,y22,i22] = Solve2OrderEquaton(parameter22);
end
root4{j}=[root21,root22];
i4{j}=[i21,i22];
root=[root,root4{j}];
i=i+i21+i22;
end
end
function [root,y,i] = Solve3OrderEquaton(parameter)
a=parameter(1);
b=parameter(2);
c=parameter(3);
d=parameter(4);
a_2=a*a;
a_3=a_2*a;
b_2=b*b;
b_3=b_2*b;
p=c/3/a-b_2/9/a_2;
q=d/2/a+b_3/27/a_3-b*c/6/a_2;
delta=q*q+p^3;
if(delta>0)
i=1;
root=nthroot(-q+sqrt(delta),3)+nthroot(-q-sqrt(delta),3)-b/3/a;
elseif(delta==0)
i=2;
root(1)=-2*nthroot(q,3)-b/3/a;
root(2)=nthroot(q,3)-b/3/a;
else
i=3;
alpha=1/3*acos(-q*sqrt(-p)/p^2);
root(1)=2*sqrt(-p)*cos(alpha)-b/3/a;
root(2)=2*sqrt(-p)*cos(alpha+2/3*pi)-b/3/a;
root(3)=2*sqrt(-p)*cos(alpha+4/3*pi)-b/3/a;
end
y=a*root.^3+b*root.^2+c*root+d;
end
function [root,y,i] = Solve2OrderEquaton(parameter)
a=parameter(1);
b=parameter(2);
c=parameter(3);
delta=b^2-4*a*c;
if(delta>0)
i=2;
root(1)=(-b+sqrt(delta))/2/a;
root(2)=(-b-sqrt(delta))/2/a;
elseif(delta==0)
i=1;
root=-b/2/a;
else
i=0;
root=[];
end
y=a*root.^2+b*root+c;
end测试代码
clc;
clear;
parameter = [1,1,1,1,0];
[root,i]=MYSolve4OrderEquaton(parameter);
[root,i]结果验证

附:一元四次方程的故事
塔尔塔利亚是意大利人,出生于1500年。他12岁那年,被入侵的法国兵砍伤了头部和舌头,从此说话结结巴巴,人们就给他一个绰号“塔尔塔利亚”(在意大利语中,这是口吃的意思),真名反倒少有人叫了,他自学成才,成了数学家,宣布自己找到了三次方程的的解法。这时,意大利数学家卡丹出场,请求塔尔塔利把解方程的方法告诉他,可是遭到了拒绝。后来卡丹对塔尔塔利假装说要推荐他去当西班牙炮兵顾问,称自己因为无法解三次方程而内心痛苦并发誓永远不泄漏塔尔塔利亚解一元三次方程式的秘密。塔尔塔利亚这才把解一元三次方程的秘密告诉了卡丹。六年以后,卡丹不顾原来的信约,在他的著作《关于代数的大法》中,将经过改进的三次方程的解法公开发表。后人就把这个方法叫作卡丹公式,塔尔塔利亚的名字反而被湮没了。
卡当公布了塔塔利亚发现的一元三次方程求根公式之后,塔尔塔利亚谴责卡当背信弃义,提出要与卡当进行辩论与比赛。这场辩论与比赛在米兰市的教堂进行,代表卡当出场的是卡当的学生费拉里。
费拉里(Ferrari L.,1522~1565)出身贫苦,少年时代曾作为卡当的仆人。卡当的数学研究引起了他费拉里对数学的热爱,当其数学才能被卡当发现后,卡当就收他作了学生。
费拉里代替卡当与塔尔塔利亚辩论并比赛时,风华正茂,他不仅掌握了一元三次方程的解法,而且掌握了一元四次方程的解法,因而在辩论与比赛中取得了胜利,并由此当上了波伦亚大学的数学教授。
一元四次方程的求解方法,是受一元三次方程求解方法的启发而得到的。一元三次方程是在进行了一元二次方程从而得解的。于是,如果能够巧妙地把一元四次方程巧妙的换元之后,把问题归结成了转化为一元三次方程或一元二次方程,就可以利用己知的公式求解了。
不幸的是,就像塔尔塔利亚发现的一元三次方程求根公式被误称为卡当公式一样,费拉里发现的一元四次方程求解方法也曾被误认为是波培拉发现的。