描述
合并 k 个升序的链表并将结果作为一个升序的链表返回其头节点。
数据范围:节点总数 0≤n≤5000,每个节点的val满足 ∣val∣<=1000
要求:时间复杂度 O(nlogn)
示例1
输入:
[{1,2,3},{4,5,6,7}]
返回值:
{1,2,3,4,5,6,7}
示例2
输入:
[{1,2},{1,4,5},{6}]
返回值:
{1,1,2,4,5,6}
思路分析:
归并排序思想
知识点1:双指针
双指针指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个指针(特殊情况甚至可以多个),两个指针或是同方向访问两个链表、或是同方向访问一个链表(快慢指针)、或是相反方向扫描(对撞指针),从而达到我们需要的目的。
知识点2:分治
分治即“分而治之”,“分”指的是将一个大而复杂的问题划分成多个性质相同但是规模更小的子问题,子问题继续按照这样划分,直到问题可以被轻易解决;“治”指的是将子问题单独进行处理。经过分治后的子问题,需要将解进行合并才能得到原问题的解,因此整个分治过程经常用递归来实现。
对于这k个链表,就相当于上述合并阶段的k个子问题,需要划分为链表数量更少的子问题,直到每一组合并时是两两合并,然后继续往上合并,这个过程基于递归:
- 终止条件: 划分的时候直到左右区间相等或左边大于右边。
- 返回值: 每级返回已经合并好的子问题链表。
- 本级任务: 对半划分,将划分后的子问题合并成新的链表。
具体做法:
- step 1:从链表数组的首和尾开始,每次划分从中间开始划分,划分成两半,得到左边n/2个链表和右边n/2个链表。
- step 2:继续不断递归划分,直到每部分链表数为1.
- step 3:将划分好的相邻两部分链表,按照两个有序链表合并的方式合并,合并好的两部分继续往上合并,直到最终合并成一个链表。
图示:
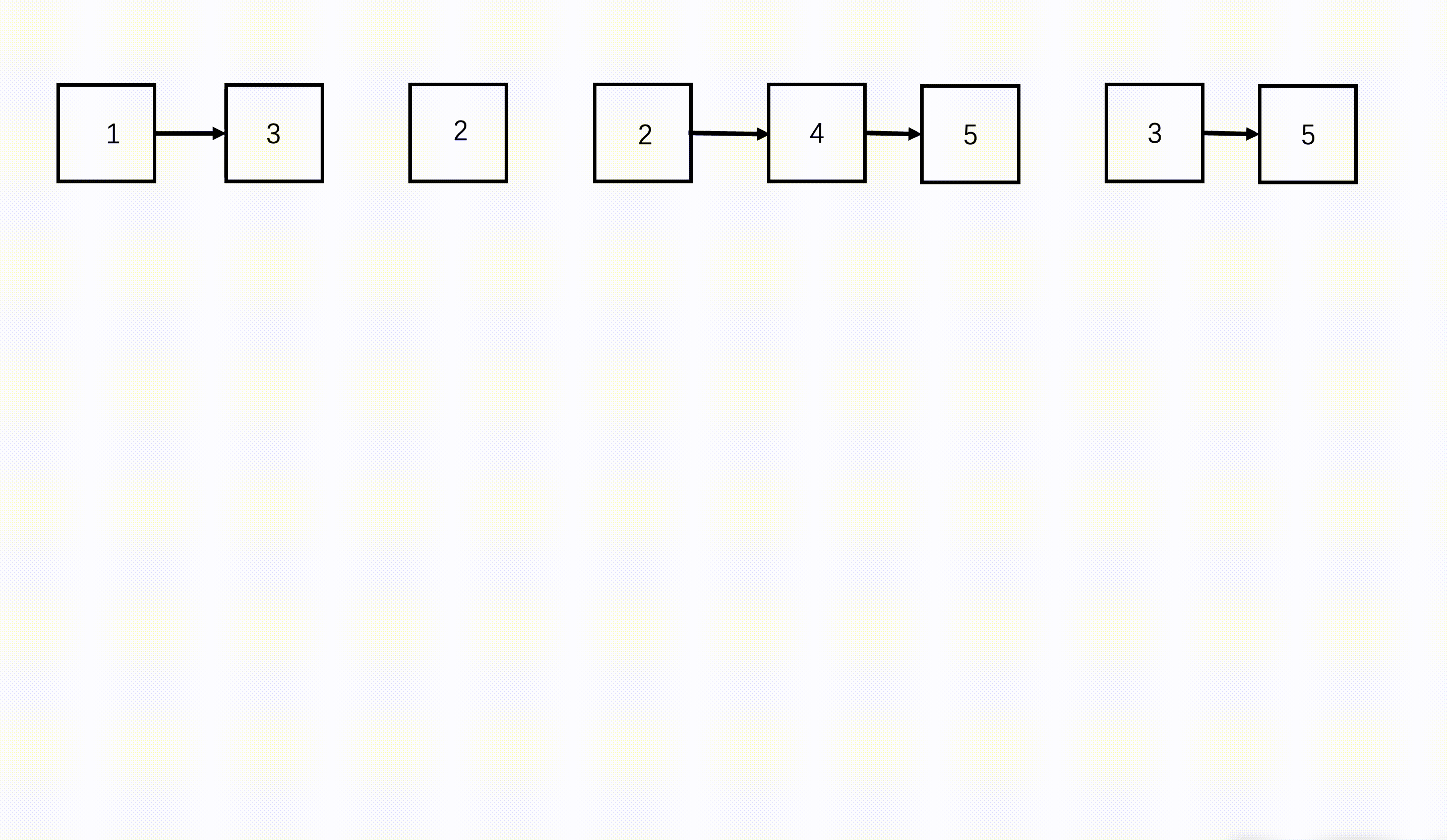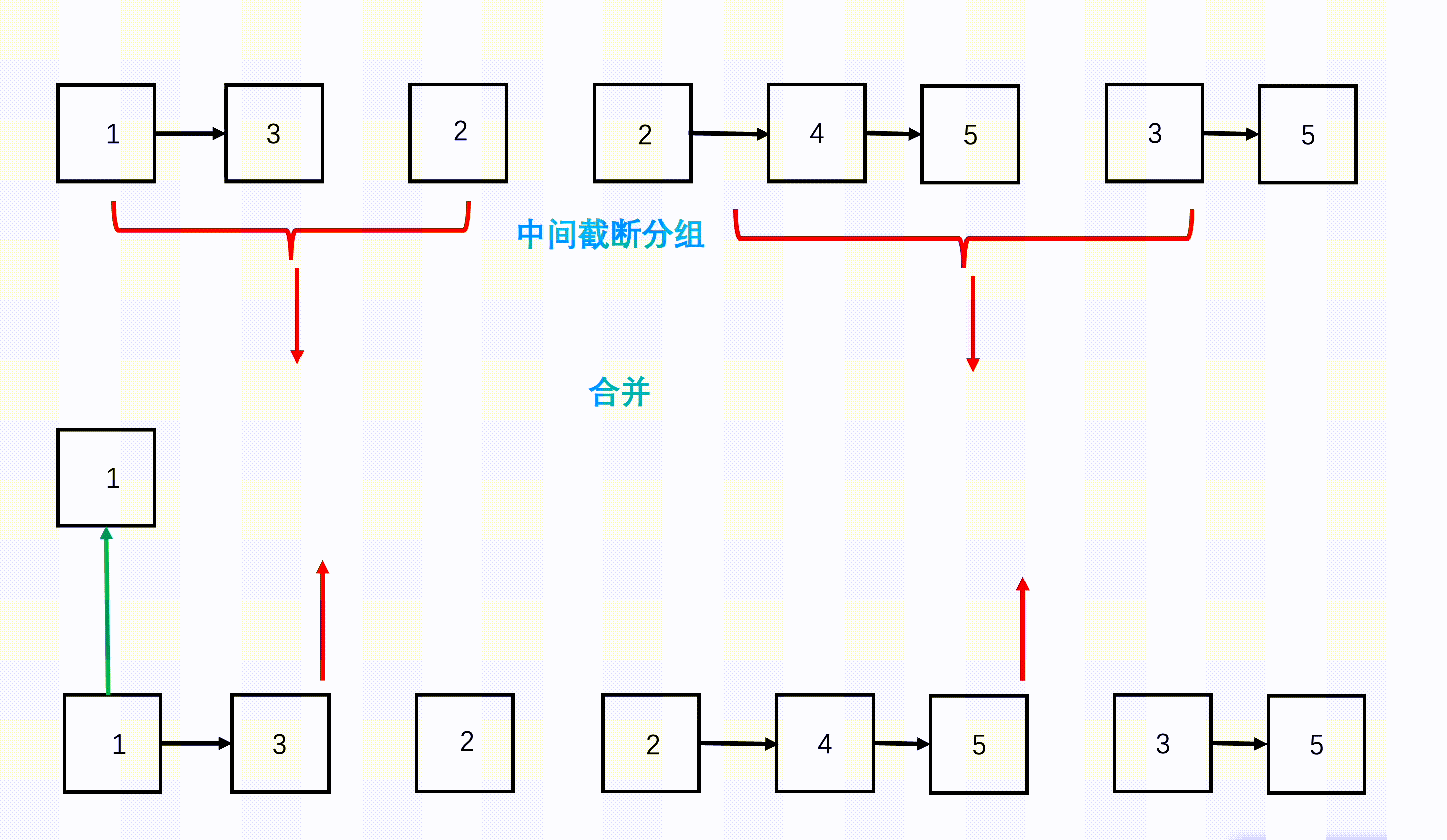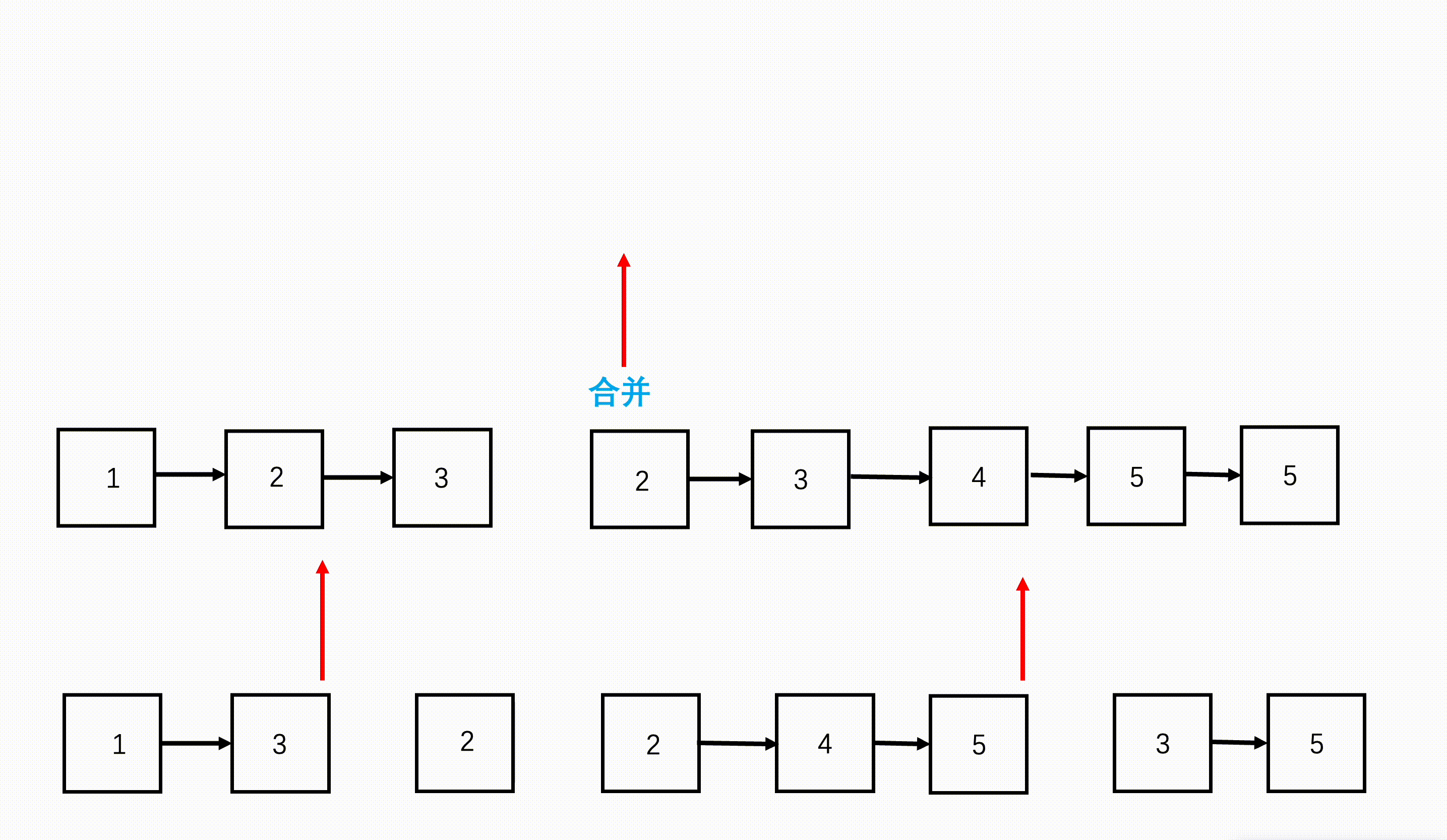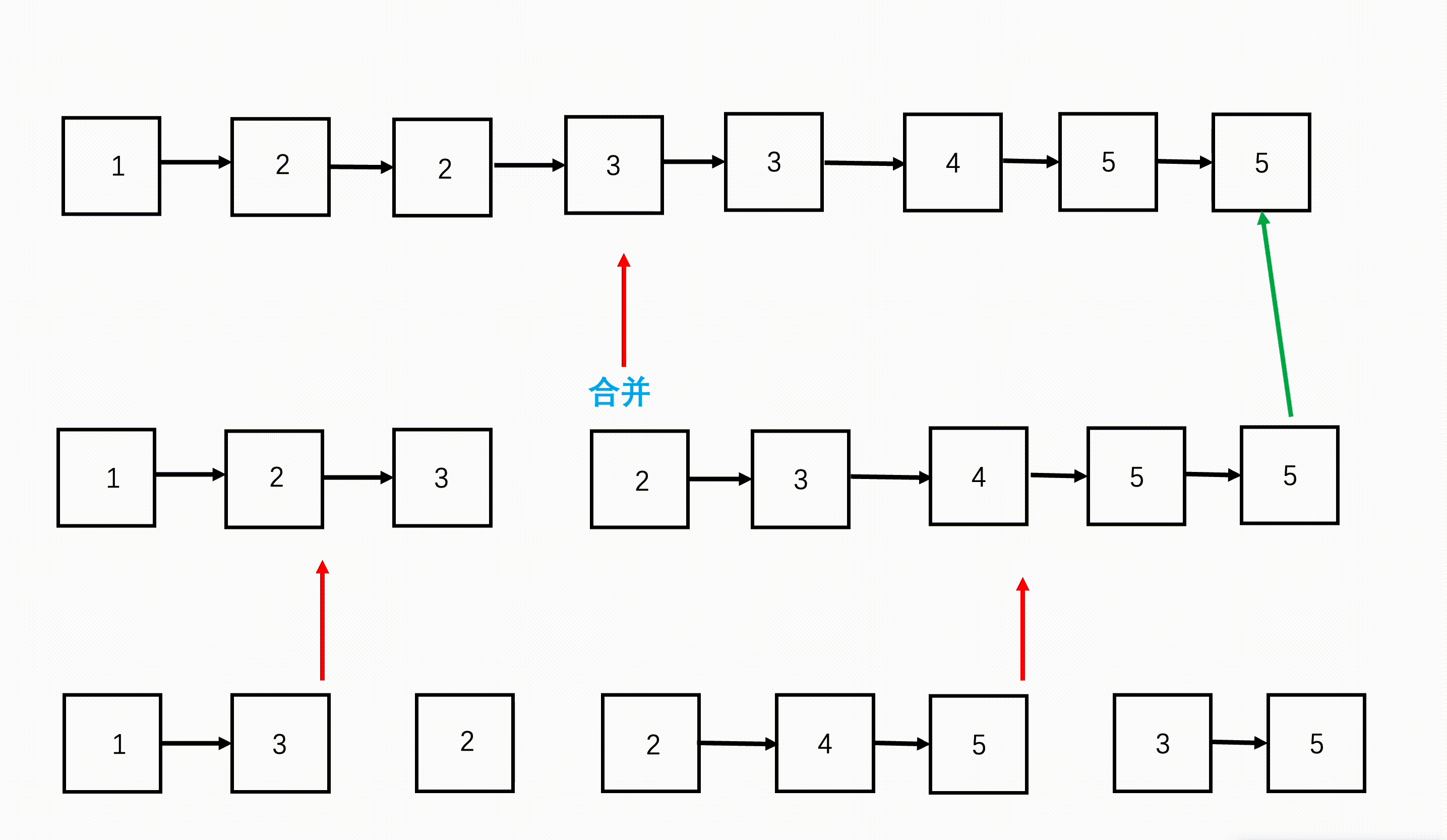
代码:
import java.util.*;
public class Solution {
//两个链表合并函数
public ListNode merge(ListNode list1,ListNode list2){
//一个已经为空了,直接返回另一个
if(list1==null){
return list2;
}
if(list2==null){
return list1;
}
//加一个表头
ListNode head=new ListNode(0);
ListNode cur=head;
//两个链表都要不为空
while(list1!=null&&list2!=null){
//取较小值的节点
if(list1.val>list2.val){
cur.next=list2;
//只移动取值的指针
list2=list2.next;
}else{
cur.next=list1;
//只移动取值的指针
list1=list1.next;
}
//指针后移,为下一次循环做准备
cur=cur.next;
}
//哪个链表还有剩,直接连在后面
if(list1!=null){
cur.next=list1;
}
if(list2!=null){
cur.next=list2;
}
//返回值去掉表头
return head.next;
}
//划分合并区间函数
public ListNode divideMerge(ArrayList<ListNode> lists,int left,int right){
if(left>right){
return null;
//中间一个的情况
}else if(left==right){
return lists.get(left);
}
//从中间分成两段,再将合并好的两段合并
int mid=(left+right)/2;
return merge(divideMerge(lists,left,mid),divideMerge(lists,mid+1,right));
}
/**
*
* @param lists ListNode类ArrayList
* @return ListNode类
*/
public ListNode mergeKLists (ArrayList<ListNode> lists) {
//k个链表归并排序
return divideMerge(lists,0,lists.size()-1);
}
}