目录

1.2 几种特殊的矩阵

 1.2.1 方阵

 1.2.2 零矩阵

 1.2.3 对角矩阵

 1.2.4 单位矩阵

 1.2.5 数量矩阵

 1.2.6 三角阵

 1.2.7 梯形阵

1.3 矩阵的运算（一）

1.3.1 相等

1.3.2 加、减法

1.3.3 数乘

1.3.4 矩阵的乘法

1.4 矩阵的运算（二）

1.4.1 方阵的正整数幂

1.4.2 矩阵的转置

1.4.3 对称阵与反对称阵

1.5 方阵的行列式

1.5.1 方阵行列式的定义

1.5.2 奇异方阵和非奇异方阵

1.5.3 方阵行列式的性质

1.6 伴随矩阵

 1.6.1 伴随矩阵的定义

 1.6.2 二阶矩阵的伴随矩阵

 1.6.3 伴随矩阵的性质

1.7 矩阵的初等变换

1.7.1 初等变换的定义

1.7.2 矩阵的等价

1.7.3 等价标准型

1.8 矩阵的秩

1.8.1 k阶子式

1.8.2 矩阵的秩的定义

1.8.3 矩阵的秩的性质

1.8.4 矩阵的秩的求法

1.8.5 矩阵等价的充要条件

1.8.6 满秩矩阵

---

1.2 几种特殊的矩阵

1.2.1 方阵

当m=n时，即矩阵的行数与列数相同时，称矩阵为方阵

1.2.2 零矩阵

1.2.3 对角矩阵

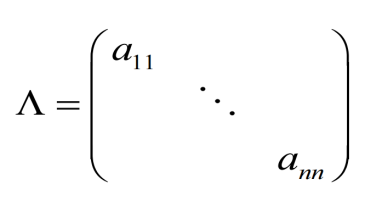
• 首先得有对角线，所以必须是方阵
• 其它没写出的元素都是零

 1.2.4 单位矩阵

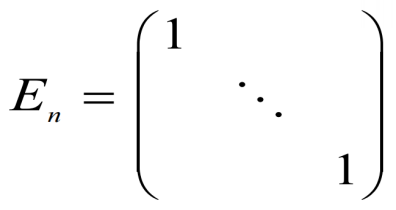
特殊的对角矩阵，对角线上的元素都是1

1.2.5 数量矩阵

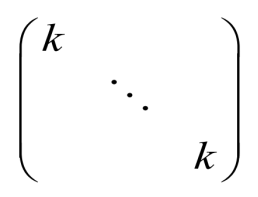
对角线上的元素是相同的数k

1.2.6 三角阵

上三角阵

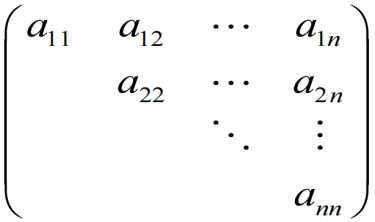
下三角阵

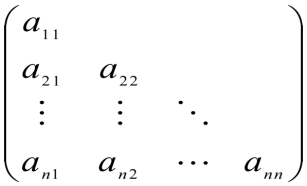
1.2.7 梯形阵

设A为非零矩阵，若非零行（即至少有一个非零元素的行）全在零行的上面

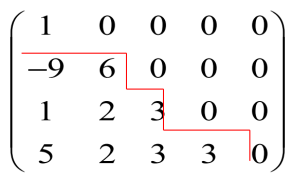
A中各非零行中第一个非零元素前面零元素的个数随行数增大而增多，则称为上梯形矩阵。简称为上梯形阵

例如

A中各非零行中最后一个非零元素后面零元素的个数随行数增大而减少，则称为下梯形矩阵，简称为下梯形阵

例如

---

1.3 矩阵的运算（一）

1.3.1 相等

相等:两个矩阵相等是指这两个矩阵有相同的行数与列数, 且对应元素相等

1.3.2 加、减法

设矩阵

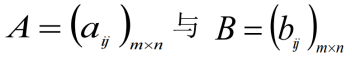
定义

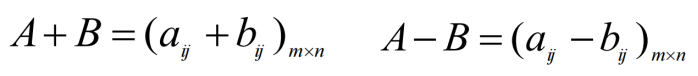
运算规律

 

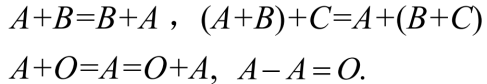
负矩阵记作 -A

 

1.3.3 数乘

A与数的乘法，简称为数乘。记作：kA

数k乘矩阵中的每一个元素

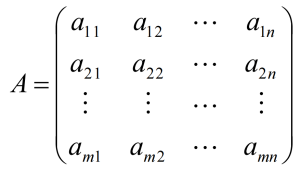
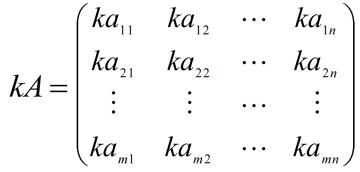
运算规律

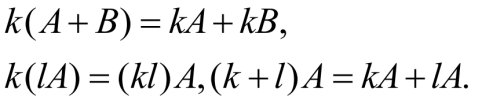
1.3.4 矩阵的乘法

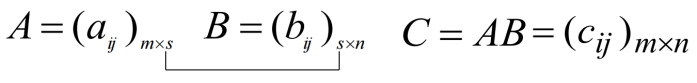
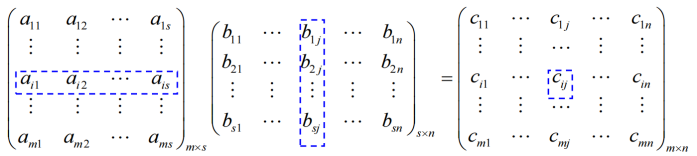 其中

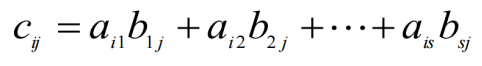
注：矩阵乘法

• 不满足交换率
• 不满足消去率
• 有非零的零因子

 运算规律

---

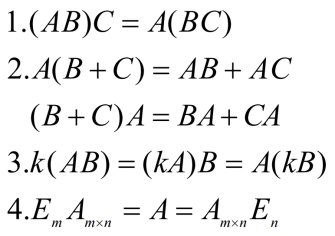
1.4 矩阵的运算（二）

1.4.1 方阵的正整数幂

 

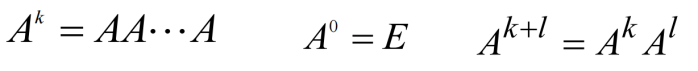
注：

只有

才有

1.4.2 矩阵的转置

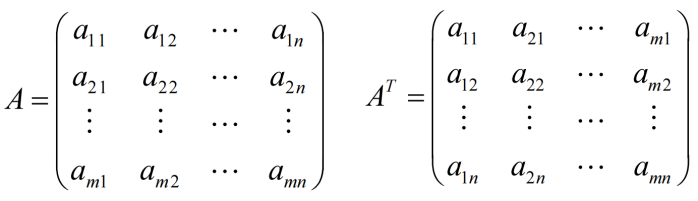
注：对角矩阵的转置是其本身

运算规律

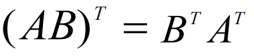
1.4.3 对称阵与反对称阵

对称矩阵满足：

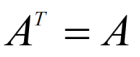
即

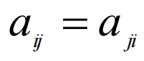
如下矩阵都是对称矩阵

反对称矩阵满足

即

 

如下矩阵就是一个反对称矩阵

 

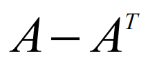
任一方阵都可以分解成对称阵与反对称阵的和

 

---

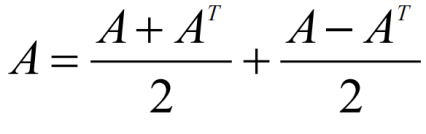
1.5 方阵的行列式

1.5.1 方阵行列式的定义

由方阵A所构成的行列式称为方阵的行列式,记为|A|或det A

1.5.2 奇异方阵和非奇异方阵

若方阵的行列式不为零,则称方阵为非奇异方阵,否则称为奇异方阵

1.5.3 方阵行列式的性质

设A、B均为n阶方阵(同阶方阵)，k为常数，则有

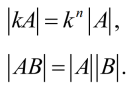
利用第一条性质可推出：

奇数阶反对称阵的行列式为零

---

1.6 伴随矩阵

1.6.1 伴随矩阵的定义

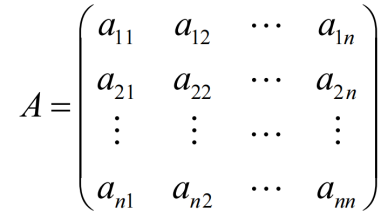
A的伴随矩阵为

注意代数余子式的顺序

 

 1.6.2 二阶矩阵的伴随矩阵

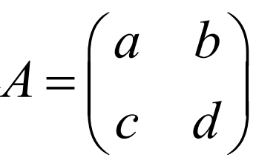
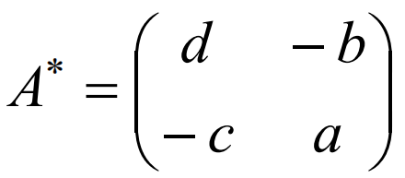
主对角线互换位置，斜对角线取相反数

1.6.3 伴随矩阵的性质

A* A的结果同上

于是我们得到

 

---

1.7 矩阵的初等变换

1.7.1 初等变换的定义

以下三种变换分别称为矩阵的第一、第二、第三种初等变换

• 对换矩阵中两行(列)的位置
• 用非零常数k乘某一行(列)
• 将矩阵的某一行(列)乘以常数k后加到某一行(列)

初等变换可以简化矩阵，如将矩阵化为梯形阵

1.7.2 矩阵的等价

对矩阵A实行有限次初等变换得到矩阵B，则称矩阵A与B等价

等价矩阵具有自反性、对称性、传递性

1.7.3 等价标准型

某个矩阵经过多次初等变换以后，得到一种最简单的矩阵，这个矩阵的左上角是一个单位矩阵，其余元素都是0，那么这个矩阵就是原来矩阵的等价标准型

任何一个矩阵都有等价标准形

---

1.8 矩阵的秩

1.8.1 k阶子式

在A中任取k行k列，位于这些行、列相交处的k^2个元素，按原次序组成的k阶行列式，称为矩阵A的k阶子式

1.8.2 矩阵的秩的定义

秩的定义:

矩阵 A 的所有不等于零的子式的最高阶数称为矩阵 A 的秩，记作 r(A)

1.8.3 矩阵的秩的性质

r(O)=0，只要A不是零矩阵, 就有 r(A)>0

矩阵经初等变换后其秩不变

1.8.4 矩阵的秩的求法

初等变换法

若其行列式的值易求出，就使用行列式来求

1.8.5 矩阵等价的充要条件

若两个矩阵有相同的秩，则这两个矩阵有相同的标准形，从而等价；反之，若两个矩阵等价，则它们的秩相同

矩阵A与B等价的充要条件是r(A)=r(B)

1.8.6 满秩矩阵

若方阵A的秩与其阶数相等，则称A为满秩矩阵；否则称为降秩矩阵

设A为满秩阵,则A的标准形为同阶单位阵 E .

若方阵A的行列式|A|≠0，则称A为非奇异矩阵

若方阵A的行列式|A| = 0，则称A为奇异矩阵

满秩⇔非奇异，降秩⇔奇异