目录
3.1 n维向量及其线性运算
3.1.1 n维向量的概念
3.1.2 向量的相等
3.1.3 n维向量的线性运算
3.1.4 线性组合
3.1.5 向量组的等价
3.2 向量组的线性相关性
3.2.1 线性相关性的定义
3.2.2 特殊情形的线性相关性
3.3 相关性的判定及有关重要结论
3.3.1 线性相关与线性组合的关系定理
3.3.2 相关性的判定定理
3.4 向量组的极大无关组
3.4.1 极大无关组的定义
3.4.2 极大无关组的性质
3.4.3 向量组的秩
3.6 向量组的极大无关组与秩的求法
3.6.1 向量组的秩的求法
3.6.2 极大无关组的求法
3.7 向量空间
3.7.1 向量空间及其子空间
3.7.2 子空间
3.7.3 向量空间的基与维数
3.7.4 向量在基下的坐标
3.8 向量组的正交性
3.8.1 向量的内积
3.8.2 向量的单位化
3.8.3 向量的正交性
3.8.4 正交向量组的性质
3.8.5 向量组的正交规范化
3.8.6 正交矩阵
3.9 施密特正交化的直观理解
3.1 n维向量及其线性运算
3.1.1 n维向量的概念
由数a1,a2,...,an组成的有序数组,称为n维向量,简称为向量
向量通常用斜体希腊字母表示

模等于1的向量被称作单位向量
3.1.2 向量的相等

3.1.3 n维向量的线性运算
线性运算满足8条运算规律
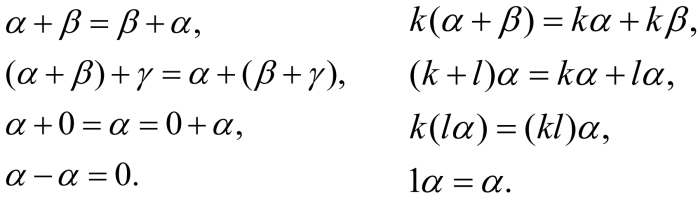
3.1.4 线性组合

3.1.5 向量组的等价
设有两个 n 维向量组

若向量组(I)中每个向量都可由向量组(II)线性表示,则称向量组(I)可由向量组(II)线性表示;
若向量组(I)与向量组(II)可以互相线性表示,则称向量组(I)与向量组(II)等价。
向量组的等价关系具有自反性、对称性、传递性
3.2 向量组的线性相关性
3.2.1 线性相关性的定义

3.2.2 特殊情形的线性相关性
- 当向量组只含一个向量时,若该向量是零向量,则它线性相关;若该向量是非零向量,则它线性无关
- 两个向量线性相关的充要条件是其对应分量成比例
- 任一含有零向量的向量组线性相关
3.3 相关性的判定及有关重要结论
3.3.1 线性相关与线性组合的关系定理
定理1

下面证明此定理

定理2

我们先证明贝塔可以被线性表示

再证明唯一性

这样就证明了唯一性
3.3.2 相关性的判定定理
定理3
在一个向量组中,若有一个部分向量组线性相关,则整个向量组也必定线性相关
一个线性无关的向量组的任何非空的部分向量组都线性无关
定理4

推论
- 当m>n时,m个n维向量线性相关
- 任意m个n维向量线性无关的充要条件是由它们构成的矩阵A的秩r(A)=m
- 任意n个n维向量线性无关的充要条件是由它们构成的方阵 A的行列式不等于零(即r(A)=n)
- 任意n个n维向量线性相关的充要条件是由它们构成的方阵 A的行列式等于零(即r(A)<n)
定理5

换句话说,就是线性无关的向量组,添加分量后仍旧线性无关
推论:r 维线性无关的向量,添加 n-r 个相应分量组成的n维向量组仍旧线性无关
3.4 向量组的极大无关组
3.4.1 极大无关组的定义

注:
线性无关向量组的极大无关组就是其本身;
向量组与其极大无关组等价;
同一个向量组的极大无关组不惟一,但它们之间是等价的
3.4.2 极大无关组的性质
定理1

推论1

推论2:任意两个线性无关的等价向量组所含向量的个数相等
定理2:一个向量组的任意两个极大无关组所含向量的个数相等
3.4.3 向量组的秩

线性无关的向量组的秩=向量的个数。
定理3
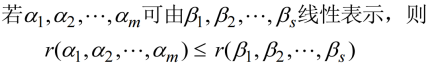
等价的向量组有相同的秩
有相同秩的两个向量组不一定等价
3.6 向量组的极大无关组与秩的求法
3.6.1 向量组的秩的求法
行秩:矩阵行向量组的秩
列秩:矩阵列向量组的秩
定理4 :矩阵的行秩与列秩相等,为矩阵的秩
推论:向量组的秩与该向量组所构成的矩阵的秩相等
这实际上给出了一个求向量组秩的方法:先将向量组构成一个矩阵,然后求矩阵的秩,这个秩就是向量组的秩
3.6.2 极大无关组的求法
列摆行变换法
列摆行变换将矩阵化为梯形阵后,秩即求出来了。这时,只要在每一高度上取一个向量,相同高度取左,即可得到极大无关组
3.7 向量空间
3.7.1 向量空间及其子空间
运算的封闭性
设V是n维向量的非空集合,如果
![]()
则称V对于向量加法及数乘两种运算封闭
设V是n维向量的非空集合,如果V对于向量加法及数乘两种运算封闭,则称集合V为n维向量空间,简称为向量空间
3.7.2 子空间
设W、V 为 向量空间,若W⊂V,则称 W 是V 的子空间
3.7.3 向量空间的基与维数
空间向量的基的定义

空间向量维数的定义
基中所含向量个数 r 称为向量空间的维数
若将向量空间视作向量组,则基就是向量组的极大线性无关组,维数就是向量组的秩。
因此,基与维数的求法类似于向量组的极大无关组与秩的求法
3.7.4 向量在基下的坐标

![]()
- 向量在一组确定的基下的坐标是惟一的。
- 向量空间的基不惟一。因此,向量在不同基下的坐标也不一样。
- 向量在一组基下的坐标一般有两种求法:待定系数法与矩阵方程法
3.8 向量组的正交性
3.8.1 向量的内积


3.8.2 向量的单位化
3.8.3 向量的正交性
若(β,α)=0,则称向量β与α正交

![]()
为正交向量组。也称为单位正交组或标准正交组
3.8.4 正交向量组的性质
一组正交向量组线性无关
线性无关的向量组不一定是正交组
3.8.5 向量组的正交规范化
施密特正交化

我们有

将一组线性无关向量组先进行施密特正交化,再进行单位化,即可得到单位正交向量组
3.8.6 正交矩阵

正交矩阵的性质

正交矩阵的判定
矩阵A为正交矩阵⇔A的行向量或列向量为单位正交向量组
3.9 施密特正交化的直观理解
参考
https://www.zhihu.com/question/31936731

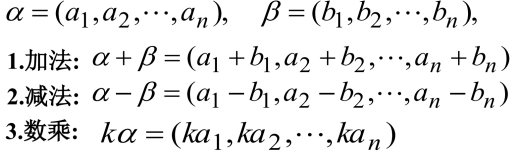

![[MQ] SpringBoot使用直连交换机Direct Exchange](https://img-blog.csdnimg.cn/885f975482b644babf9b9b322e0e68f9.png)



![[附源码]Python计算机毕业设计_旅游系统](https://img-blog.csdnimg.cn/3582fcc7d75046ecb21adbf1848dfd89.png)