一、说明
二、假想的厨师
想象一下,在任何一天,你决定复制你在一家著名餐厅吃过的美味佳肴。你完全记得这种美味的味道。基于此,您在线搜索食谱并尝试在家中复制它。
让我们将您在餐厅吃到的美味佳肴的味道表示为 T,这将代表预期的口味,即您的目标。根据你在网上找到的食谱,你希望实现这个目标,即味道T。
要复制此食谱,您需要按照所有指示的步骤进行操作,使用所有成分、必要的温度、烹饪时间等。让我们将所有这些方法和成分表示为 X。
完成整个过程后,您将品尝这道菜。此时,您判断它是否与预期的味道T相似。你注意到它比预期的更咸或更甜。您在家中复制的美味佳肴的味道将用 Y 表示。
因此,在意识到味道与目标 T 不同时,您可以根据味道 Y 分配一个定量度量,以衡量它与目标味道的差异程度。换句话说,你可以加更多的盐或更少的盐,更多的调味料或更少的调味料。
T 和 Y 之间的差值可以定义为误差 E。T 和 Y 之间的区别是由你的味觉记忆做出的。因此,您的味觉此时执行特定功能,我们可以将其定义为 P(Y) = E。换句话说,当体验到味觉 Y 时,味觉会根据目标味觉 T 分配误差 E。
有了误差 E 的定量度量,我们可以每天重现这个配方,这样随着时间的推移,误差 E 就会减少。换句话说,目标口味 T 和口味 Y 之间的距离减小,直到 T = Y。
基于这个假设的场景,我们可以将错误定义为与观察到的现实不一致的判断,其中总有一个函数执行判断动作。因此,在上述情况下,味觉和记忆创造了这种判断功能。
在这种特定情况下,学习行为的特点是能够减少错误。换句话说,它是以不同方式与复制对象交互的能力,以减少判断功能的输出。
三、厨师的专业知识
回到假设的情况,我们有食谱所示的成分和方法 X。所有的食材和设备都与餐厅使用的相同;因此,结果完全取决于您正确操纵它们以实现目标口味 T 的能力。
换句话说,你操纵 X 来获得 Y。因此,我们可以定义 U 本质上是一个将 X 转换为 Y 的函数,表示为 f(X) = Y。
函数f(X)代表操纵成分的行为,也取决于你的大脑如何运作。换句话说,如果你有烹饪经验,你会发现把X变成Y更容易。
让我们将 W 定义为神经元的权重或操纵 X 的神经能力。如果 W 已经根据烹饪经验进行了预先调整,则将 X 转换为 Y 会更容易。否则,我们将需要调整 W,直到我们可以将 X 转换为 Y。
因此,我们知道 f(X) = Y 也取决于 W,即我们可以在 f(X) = WX 中线性表示它。
因此,我们的目标是发现如何修改 W,直到生成的 Y 非常接近或等于 T。换句话说,我们如何调整 W,直到误差 E 显着减小或变为零。
四、成本函数
评估结果与预期结果之间差值的函数是成本函数。将食材和烹饪方法转化为美味的功能是我们的模型,它可以是人工神经网络,也可以是其他机器学习模型。

式(1)
在等式(1)中,成本函数E的定义,它取决于n个权重w。换句话说,它是一个根据 w 的值指示错误的函数。在未调整所有 n 个权重 w 的特定情况下,误差 E 的值会很大。相反,在权重调整正确的情况下,误差 E 的值将很小或为零。
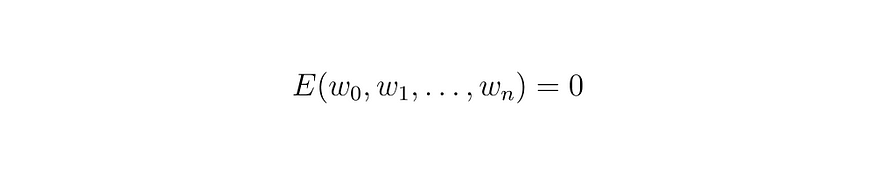
方程(2)
因此,我们的目标是找到 n 个权重 w 的值,使得上述条件为真。
五、梯度
为了便于理解我们将如何做到这一点,我们将定义以下函数:
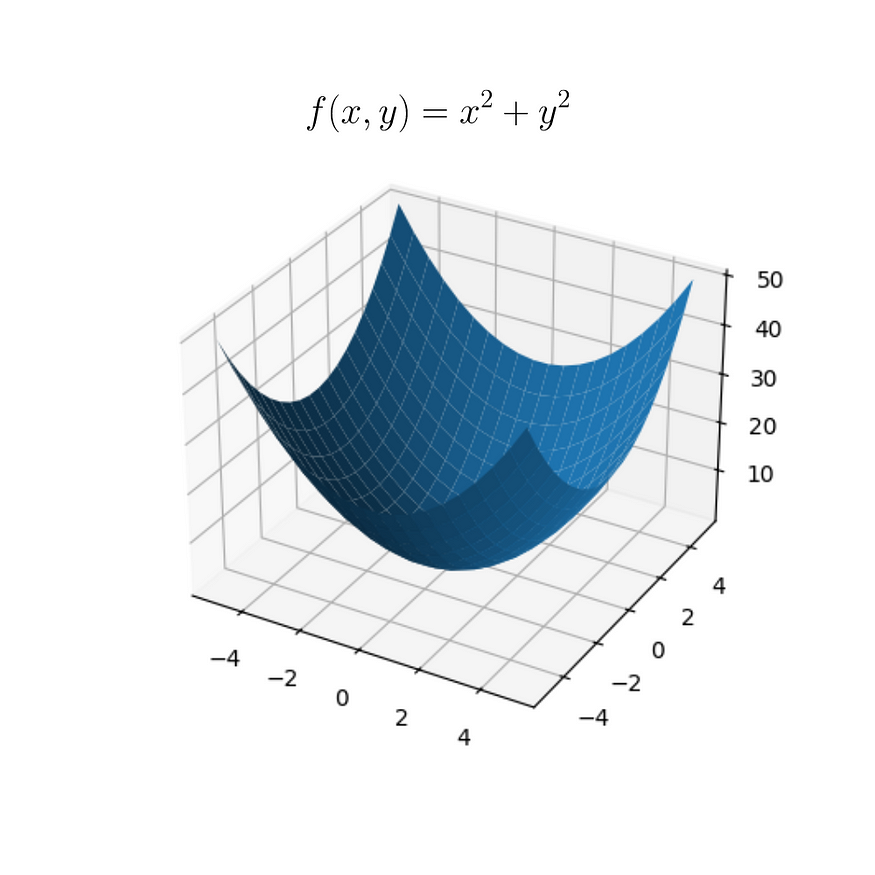
图片(1)
因此,我们直观地知道,当 x = 0 且 y = 0 时,f(x, y) = 0。但是,我们想要一种算法,在给定随机 x 和 y 值的情况下,调整 x 和 y 的值,直到函数 f(x, y) 等于零。
为了实现这一点,我们可以使用函数的梯度。在向量演算中,梯度是一个向量,它指示方向和大小,通过从指定点的位移,我们获得了数量值的最大可能增加。
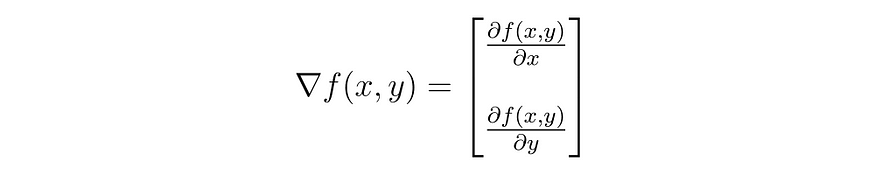
式(3)
也就是说,通过将梯度应用于函数 f(x, y),我们得到了一个向量,如等式 (3) 所示,它告知如何增加 x 和 y 的值以使 f(x, y) 的值增长。但是,我们的目标是找到函数 f(x, y) = 0 所需的 x 和 y 值。因此,我们可以使用负梯度。
下面是函数 f(x, y) 的两维表示,其中着色表示 z 的值。使用负梯度,我们看到向量指向函数的最小值。
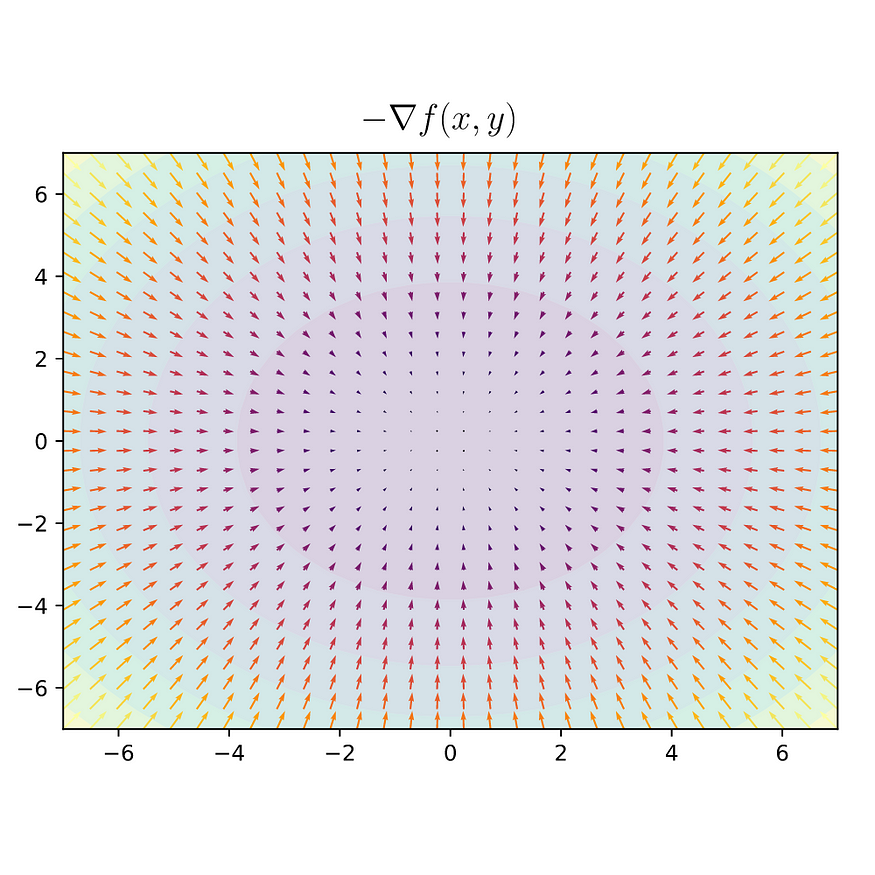
图片(2)
基于此,我们可以开发一种方法,使用函数 f(x, y) 的梯度场更新 x 和 y,以找到 f(x, y) = 0 的必要值。
六、学习的证明
我们将定义一个简单的函数 f(x) 用于算法测试。我们的目的是找到此函数的最小值。为此,我们可以应用 f(x) 的梯度。
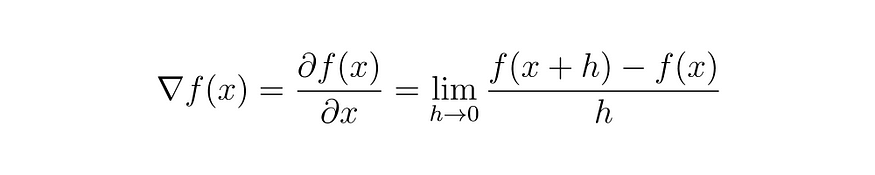
方程(4)
上面,我们有函数 f(x) 的梯度。我们不会在本文中深入定义导数的概念,但我们建议您阅读有关其定义以及为什么我们可以以这种方式表示它。
知道 h 趋于零,我们可以将 f(x) 的梯度表示为如下:
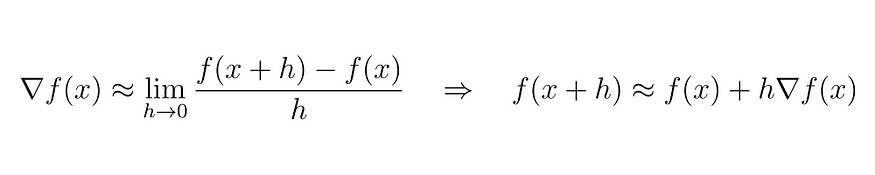
方程 (5)
基于此,我们可以用以下术语替换 h:
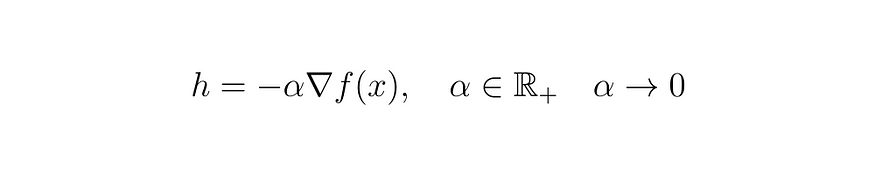
式 (6)
我们定义元素 alpha 以保持项 h 的必要性,其中 alpha 必须严格为正,并且始终趋于零,与项 h 相同。将新关系代入导数的定义中,我们有:
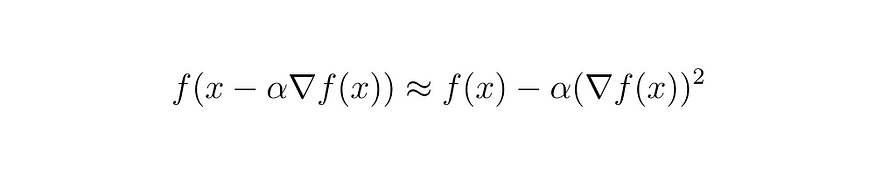
式 (7)
现在我们有一个宝贵的关系来证明。我们知道任何元素的平方都是正的。根据这个概念,需要用减去 alpha 乘以 f(x) 的梯度来代替 h。
所以:
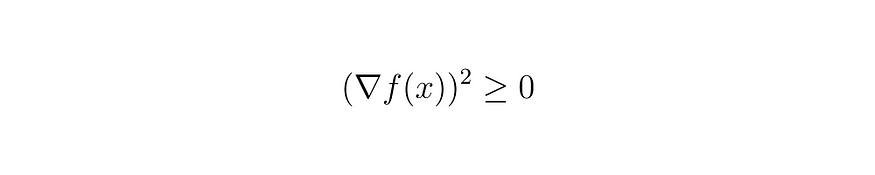
方程 (8)
因此,只要 alpha 始终为正值,我们就可以判断 (8) 中的条件为真。
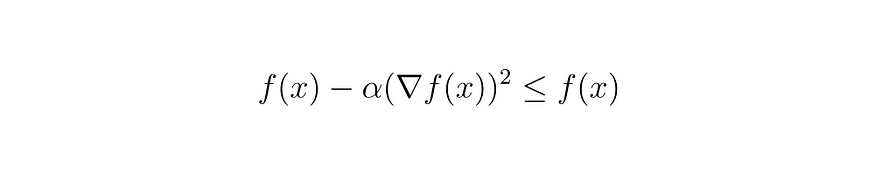
方程 (9)
也就是说,用严格的正值减去 f(x) 的值将始终小于 f(x) 的原始值。因此,我们可以使用式(7)和(9)将其替换为以下关系:
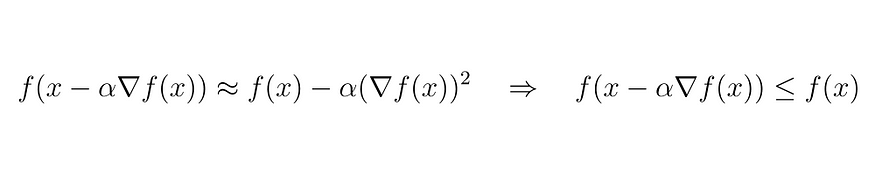
方程 (10)
因此,对于如何更新 x 的值,使函数 f(x) 至少小于其先前的状态,我们有一个经过验证的关系。
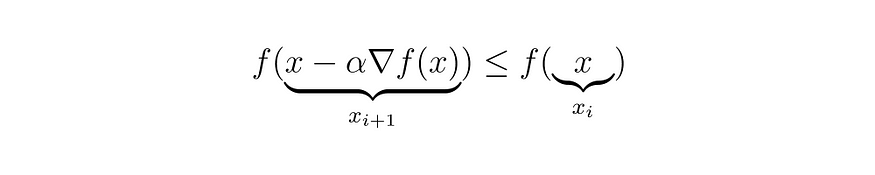
方程 (11)
因此,我们知道如何减小当前的 x 以满足不等式 (11):
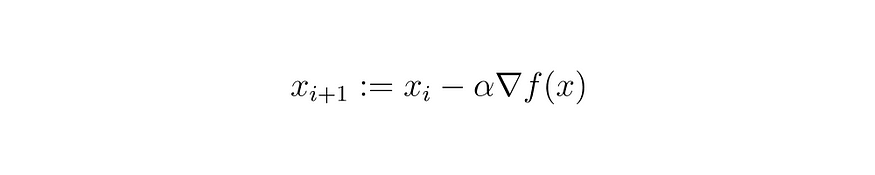
方程 (12)
为了确认这种关系的有效性,我们可以将此方法应用于 img 中的函数 f(x, y)。(1)我们知道谁的行为。所以:

方程 (13)
将此算法多次应用于函数 f(x, y),我们期望看到函数的值减小,直到达到最小值。为此,我们进行了一个模拟,此外,我们还将噪声应用于更新的 x 和 y 的分配,以可视化 f(x, y) 值的减少。
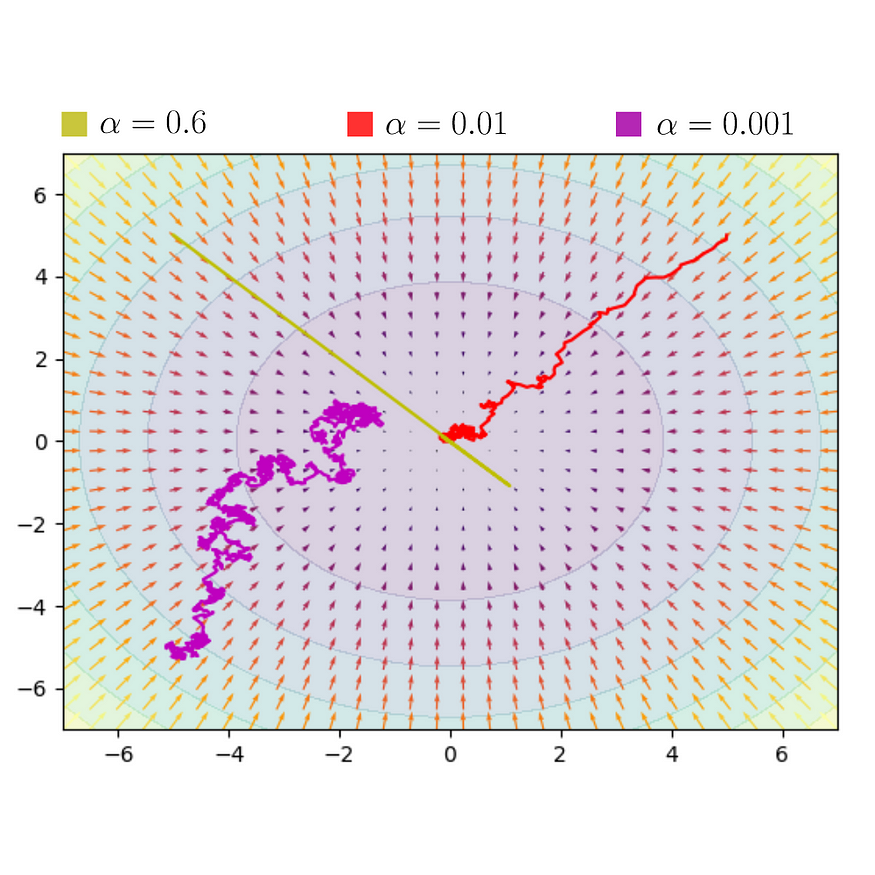
图片(3)
请注意,当 alpha 的值趋于零时,我们观察到 x 和 y 的值趋于函数的最小值。当这不是真的时,例如,在 alpha = 0.6 时,我们观察到找到函数 f(x, y) 的最小值有一定的困难。
七、梯度下降
该算法被称为“梯度下降”或“最陡下降方法”,是一种优化方法,用于找到函数的最小值,其中每一步都在负梯度方向上进行。此方法不保证会找到函数的全局最小值,而是局部最小值。
关于找到全局最小值的讨论可以在另一篇文章中展开,但在这里,我们已经从数学上展示了梯度如何用于此目的。
现在,将其应用于依赖于 n 个权重 w 的成本函数 E,我们有:
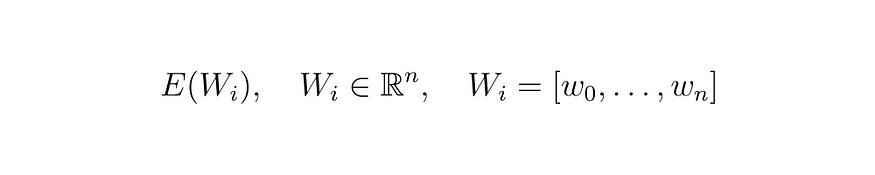
方程 (14)
为了根据梯度下降更新 W 的所有元素,我们有:

方程 (15)
对于向量 W 的任何第 n个元素 w,我们有:
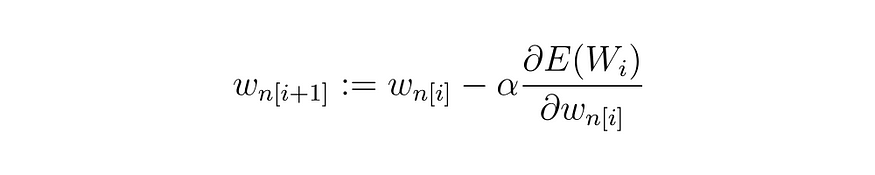
方程 (16)
因此,我们有了自己的理论学习算法。从逻辑上讲,这并不适用于厨师的假设想法,而是适用于我们今天所知道的众多机器学习算法。
八、结论
根据我们所看到的,我们可以得出结论,理论学习算法的演示和数学证明。这种结构适用于许多学习方法,例如 AdaGrad、Adam 和随机梯度下降 (SGD)。
此方法不能保证在成本函数产生零结果或非常接近它的结果时找到 n 权重值 w。但是,它向我们保证,将找到成本函数的局部最小值。
为了解决局部最小值的问题,有几种更鲁棒的方法,例如 SGD 和 Adam,它们通常用于深度学习。然而,理解基于梯度下降的理论学习算法的结构和数学证明将有助于理解更复杂的算法。