交互式散点图，快速提升你的PPT观赏性

一、散点图基础概念

散点图是一种非常直观且功能强大的图表，用于探索和展示两个数值变量之间的相关性。这种图表通过在二维平面上绘制数据点，使得观察者能够一眼看出变量间的潜在联系。

1-1：散点图的构成

X轴（横轴）：通常用于表示自变量或解释变量，每个数据点在X轴上的坐标对应其第一个变量的数值。
Y轴（纵轴）：用于表示因变量或响应变量，每个数据点在Y轴上的坐标对应其第二个变量的数值。
数据点：每个数据点在图表上的位置由其在两个变量上的数值决定，形成了散点图的主要视觉元素。

1-2：散点图的应用

相关性分析：散点图可以揭示两个变量之间的线性关系、非线性关系，或者没有明显关系。
趋势识别：通过观察数据点的分布模式，可以识别出变量间增加、减少或波动的趋势。
异常值检测：散点图上远离大多数数据点的个别点可能表示数据中的异常值或离群点。
分布特征观察：散点图可以帮助观察数据的分布特征，如对称性、偏态等。

1-3：散点图的高级特性

颜色和形状编码：为了进一步区分数据点，可以根据第三个变量给数据点上色或改变形状。
数据平滑：在散点图上添加趋势线或回归线，可以帮助观察数据的总体趋势。
透明度调整：当数据点过多且重叠时，调整数据点的透明度可以更清晰地展示数据的密度。
交互式元素：在交互式图表中，用户可以通过悬停或点击来获取特定数据点的详细信息。

1-4：散点图的制作

数据准备：确保数据集中包含两个数值变量，以及可能的分类变量用于颜色或形状编码。
选择图表工具：使用统计软件或编程语言（如R、Python的matplotlib或seaborn库）来创建散点图。
调整图表参数：根据需要调整轴标签、图例、标题等，确保图表信息清晰且易于理解。
分析和解释：制作完成后，对散点图进行分析，提取有关变量关系的见解，并据此做出解释。

1-5：代码演示

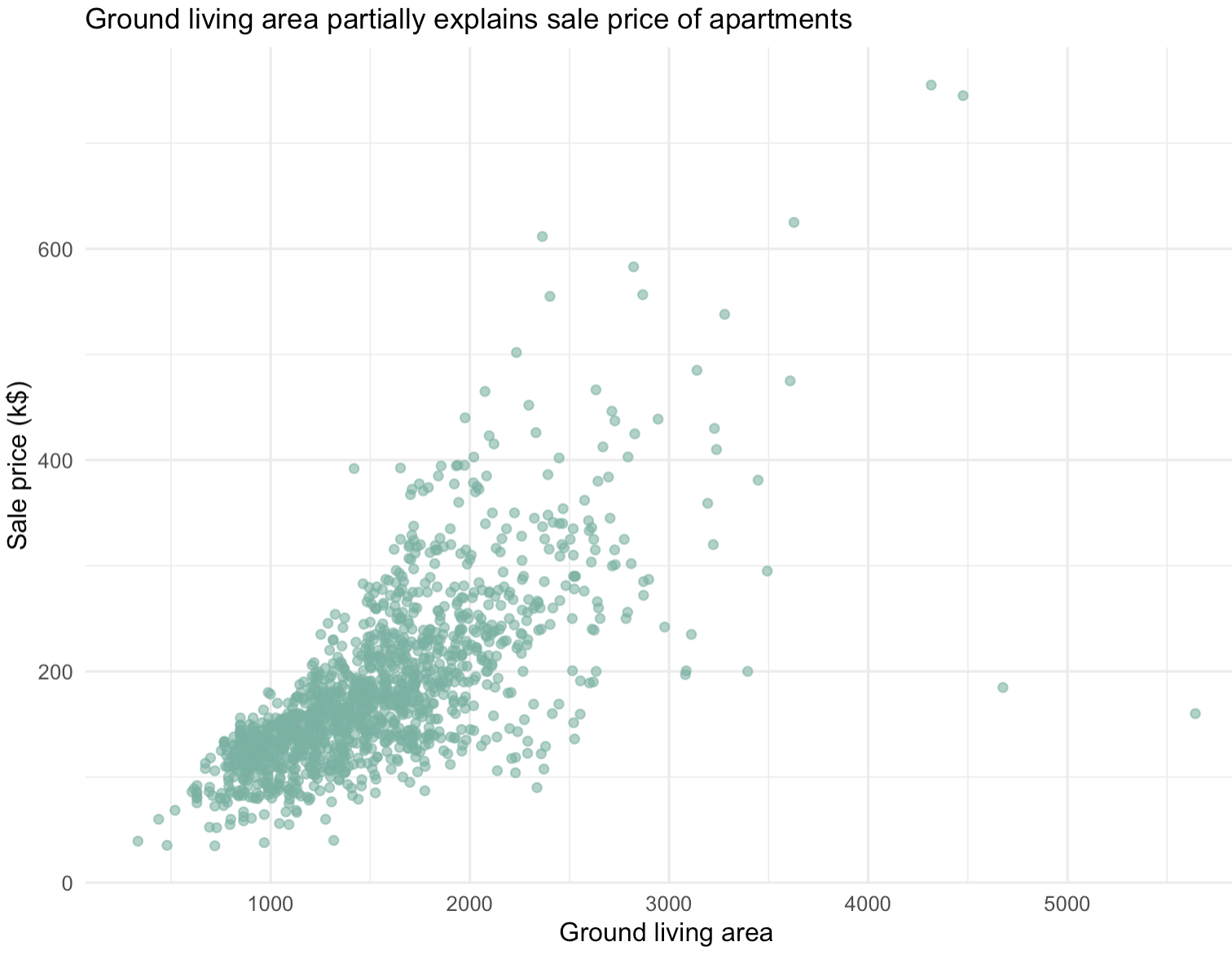
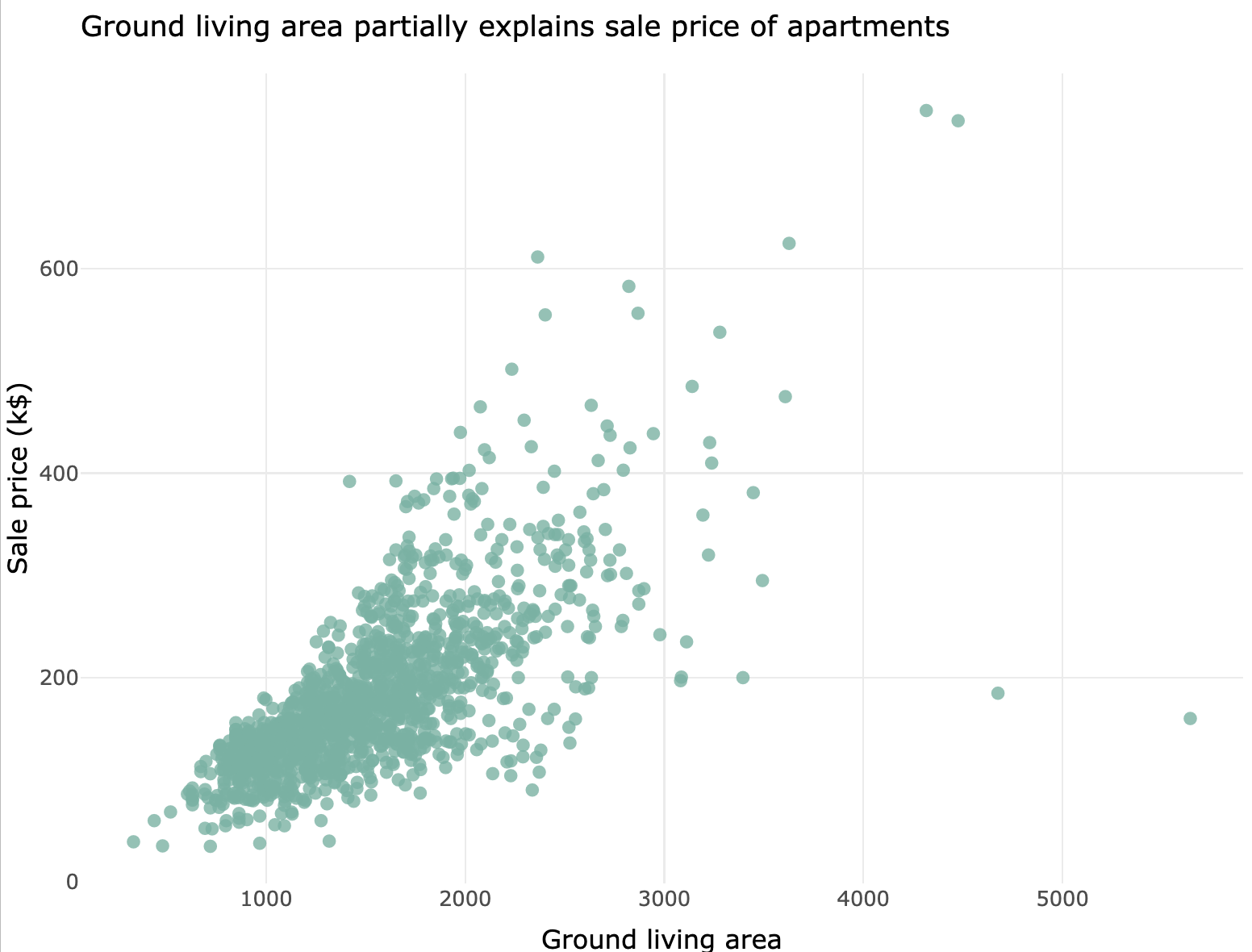
以下是一个示例，考虑了1460套公寓的价格及其地面居住面积。该数据集来自Kaggle机器学习竞赛。

# 导入所需的库
library(tidyverse) # 数据处理和绘图
library(hrbrthemes) # 提供美观的主题
library(viridis) # 提供颜色调色板

# 从GitHub加载数据集
data <- read.table("https://raw.githubusercontent.com/holtzy/data_to_viz/master/Example_dataset/2_TwoNum.csv", header=T, sep=",") %>% 
  dplyr::select(GrLivArea, SalePrice) # 选择需要的列：地面居住面积和销售价格

# 绘制散点图
data %>%
  ggplot( aes(x=GrLivArea, y=SalePrice/1000)) + # 设置x轴为地面居住面积，y轴为销售价格（千美元）
    geom_point(color="#69b3a2", alpha=0.6) + # 添加散点，颜色为#69b3a2，透明度为0.6
    ggtitle("Ground living area partially explains sale price of apartments") + # 添加标题
    theme_minimal() + # 使用简洁的主题
    theme(
      plot.title = element_text(size=12) # 设置标题字体大小为12
    ) +
    ylab('Sale price (k$)') + # 设置y轴标签
    xlab('Ground living area') # 设置x轴标签

二、检测变量关系

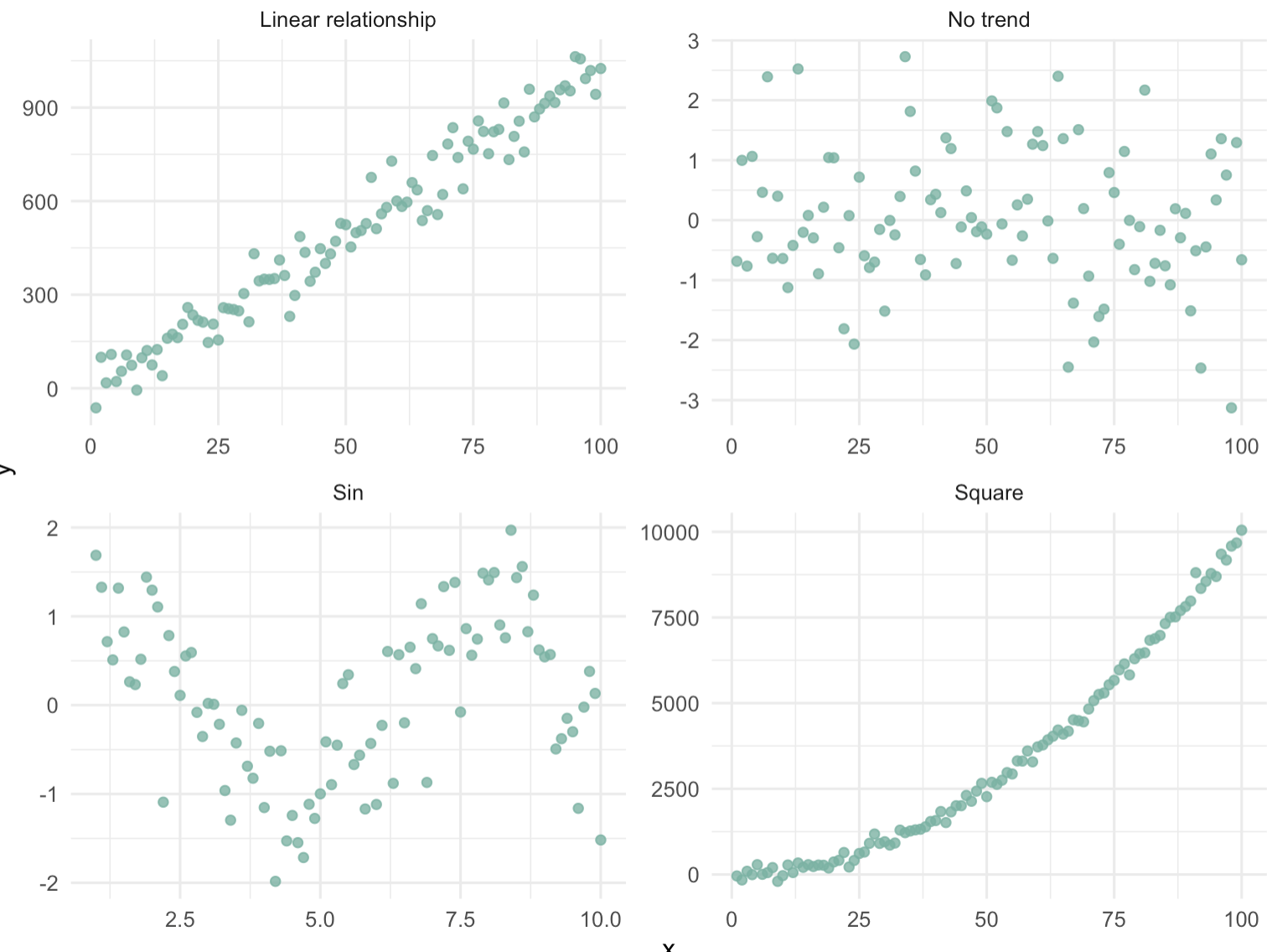
散点图是一种多功能的可视化工具，它不仅可以揭示变量之间的线性关系，还可以揭示更多复杂的关系和数据特征。

2-1：散点图的多维度分析

正线性关系：
- 在正线性关系中，数据点呈现出从左下角到右上角的上升趋势，这种模式表明随着一个变量的增加，另一个变量也相应增加。
负线性关系：
- 与正线性关系相反，负线性关系中数据点呈现出从左上角到右下角的下降趋势，表明一个变量的增加伴随着另一个变量的减少。
无关系：
- 当数据点在散点图上随机分布，没有明显的上升或下降趋势时，这表明两个变量之间可能不存在线性关系。
非线性关系：
- 非线性关系可以通过数据点形成的曲线或复杂图案来识别，如S形、波浪形或其他不规则形状，这表明变量间的关系可能需要更复杂的数学模型来描述。
群组模式：
- 群组模式可能表现为数据点在特定区域的聚集，这可能指示数据中存在某些未观察到的分类变量或自然分组。
异常值：
- 异常值在散点图上表现为远离其他数据点的孤立点，它们可能是由于测量误差、数据录入错误或真实的离群现象。

2-2：散点图的统计分析

相关系数：
- 相关系数（如皮尔逊相关系数）是衡量两个变量之间线性关系强度和方向的统计指标。然而，高相关系数并不总是意味着因果关系。
回归分析：
- 回归分析可以用来拟合一个模型，描述Y变量如何依赖于X变量。这可以是线性回归，也可以是更复杂的非线性回归模型。
模型诊断：
- 通过散点图可以进行模型诊断，检查拟合的模型是否合理。残差图可以帮助识别模型假设的违反情况。

2-3：散点图的高级可视化技术

颜色编码：
- 通过颜色编码，可以展示数据点的额外维度，如时间序列的不同阶段或不同类别的成员。
大小编码：
- 数据点的大小可以表示第三个变量的数值大小，为散点图添加更多信息层次。
透明度调整：
- 在数据点非常密集的区域，调整透明度可以帮助区分数据点的密度和分布。
交互式元素：
- 交互式散点图允许用户通过工具提示、点击或拖动来探索数据点的详细信息，提供更深入的数据分析体验。

2-4：代码演示

# 创建数据
d1 <- data.frame(x=seq(1,100), y=rnorm(100), name="No trend") # 创建无趋势数据
d2 <- d1 %>% mutate(y=x*10 + rnorm(100,sd=60)) %>% mutate(name="Linear relationship") # 创建线性关系数据
d3 <- d1 %>% mutate(y=x^2 + rnorm(100,sd=140)) %>% mutate(name="Square") # 创建平方关系数据
d4 <- data.frame( x=seq(1,10,0.1), y=sin(seq(1,10,0.1)) + rnorm(91,sd=0.6)) %>% mutate(name="Sin") # 创建正弦关系数据
don <- do.call(rbind, list(d1, d2, d3, d4)) # 将四个数据集合并为一个数据框

# 绘图
don %>%
  ggplot(aes(x=x, y=y)) + # 设置x轴和y轴的变量
    geom_point(color="#69b3a2", alpha=0.8) + # 添加散点图，颜色为#69b3a2，透明度为0.8
    theme_minimal() + # 使用简洁的主题
    facet_wrap(~name, scale="free") # 根据'name'列分面显示，每个子图的尺度自由

三、交互性

交互性是散点图的一大优势。它允许用户放大图形的特定部分，以检测更精确的模式。同时，它还允许用户悬停于点上以获取更多关于它们的信息。

# 导入plotly库，它可以将任何ggplot2图形转换为交互式图形
library(plotly)

# 创建一个新的数据框，其中包含用于悬停信息的文本
p <- data %>%
  mutate(text=paste("Apartment Number: ", seq(1:nrow(data)), "
Location: New York
Any other information you need..", sep="")) %>%
  ggplot( aes(x=GrLivArea, y=SalePrice/1000, text=text)) + # 设置x轴、y轴和悬停文本
    geom_point(color="#69b3a2", alpha=0.8) + # 添加散点图，颜色为#69b3a2，透明度为0.8
    ggtitle("Ground living area partially explains sale price of apartments") + # 添加标题
    theme_minimal() + # 使用简洁的主题
    theme(
      plot.title = element_text(size=12) # 设置标题字体大小为12
    ) +
    ylab('Sale price (k$)') + # 设置y轴标签
    xlab('Ground living area') # 设置x轴标签

# 使用ggplotly函数将ggplot2图形转换为交互式图形，并设置悬停信息为"text"
ggplotly(p, tooltip="text")

在RStudio中是可以交互的，这里无法显示，后期我会介绍如何运用交互式图表提升自己的演示效果。

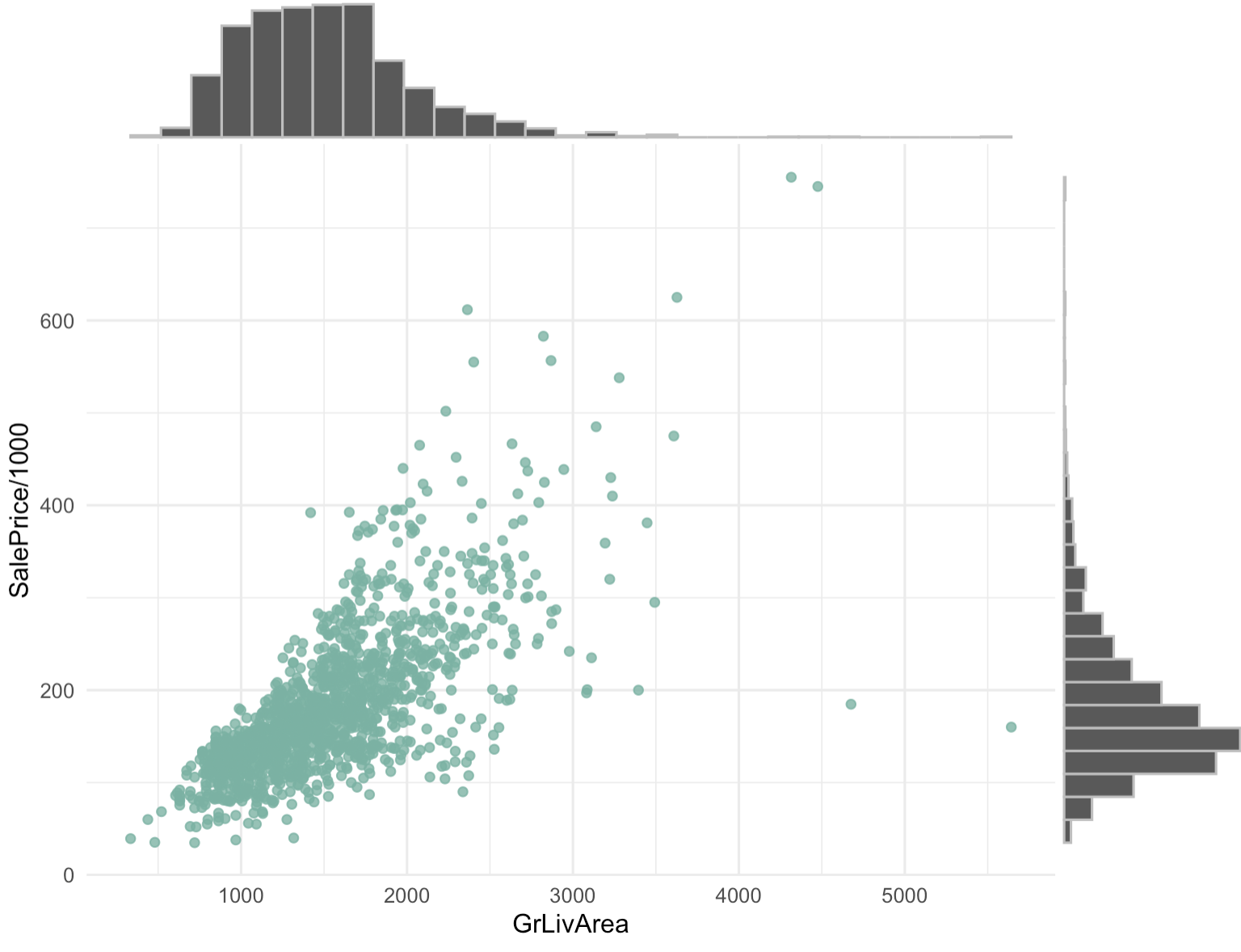
四、边缘分布

散点图有时会辅以边缘分布。这确实为图形增添了洞察力，揭示了两个变量的分布情况。

边缘分布通常以小图表的形式附加在主散点图的边缘，可以是直方图、密度图或箱线图等形式。这些小图表展示了每个变量在独立于另一个变量的情况下的分布特征，如下：

X轴边缘分布：展示了所有数据点在X变量上的分布情况，帮助观察者了解X变量的频率分布、集中趋势和离散程度。
Y轴边缘分布：展示了所有数据点在Y变量上的分布情况，同样有助于观察者了解Y变量的统计特性。

通过结合散点图和边缘分布，分析者可以更全面地理解数据集。这种组合不仅显示了变量之间的关联性，还提供了每个变量的单独统计信息，从而增强了数据解释的深度和准确性。例如，如果散点图显示变量之间存在线性关系，边缘分布则可以揭示这种关系是否受到极端值或偏态分布的影响。

# 导入ggExtra库，它提供了一些额外的ggplot2功能，如添加边际直方图
library(ggExtra)

# 创建一个ggplot2散点图
p <- data %>%
  ggplot( aes(x=GrLivArea, y=SalePrice/1000)) + # 设置x轴和y轴的变量
    geom_point(color="#69b3a2", alpha=0.8) + # 添加散点图，颜色为#69b3a2，透明度为0.8
    theme_minimal() + # 使用简洁的主题
    theme(
      legend.position="none" # 不显示图例
    )

# 使用ggExtra库的ggMarginal函数为散点图添加边际直方图，类型为直方图，颜色为灰色
ggExtra::ggMarginal(p, type = "histogram", color="grey")