算法介绍:
广度优先搜索(Breadth-First Search,简称BFS)是一种遍历或搜索树和图的算法,也称为宽度优先搜索,BFS算法从图的某个节点开始,依次对其所有相邻节点进行探索和遍历,然后再对这些相邻节点的相邻节点进行探索,直到遍历完所有的节点。BFS算法使用队列来辅助实现,将起始节点放入队列中,然后依次取出队列中的节点,访问其相邻节点,并将其加入队列。这样可以保证从起始节点出发,依次按照距离顺序遍历节点。BFS常用于寻找最短路径,因为它按照从起点到每个节点的距离来探索节点。
在ACM、蓝桥杯等著名竞赛中BFS算法是比较重要的,特别是在蓝桥杯中每一年几乎都要考DFS/BFS算法。BFS算法在OI赛中用处非常大,可以通过DFS/BFS暴力的方式可以拿到部分分数,蓝桥杯一般可以拿到20%的分数,有的甚至高达50%,是暴力得分的不二之选。

基本步骤:
BFS算法通常使用队列来实现,BFS算法的具体步骤如下:
- 创建一个队列,将起始节点加入队列;
- 创建一个集合,用于存储已经访问过的节点;
- 从队列中取出一个节点,并将其标记为已访问;
- 访问该节点的所有相邻节点,如果相邻节点未被访问,则将其加入队列;
- 重复步骤3和步骤4,直到队列为空。
BFS算法可以用来解决一些问题,例如图的遍历、最短路径搜索等。由于BFS算法保证了按照距离顺序遍历节点,因此可以用来寻找最短路径。另外,BFS算法还可以用来判断图是否连通,即从一个节点是否可以到达另一个节点。
图解算法:
下面放一张我们学校ACM在大一培训时使用的一张动态BFS/DFS步骤图。注:红色遍历为BFS、黄色遍历为DFS。(绿色为起点,紫色为终点,黑色为障碍物)

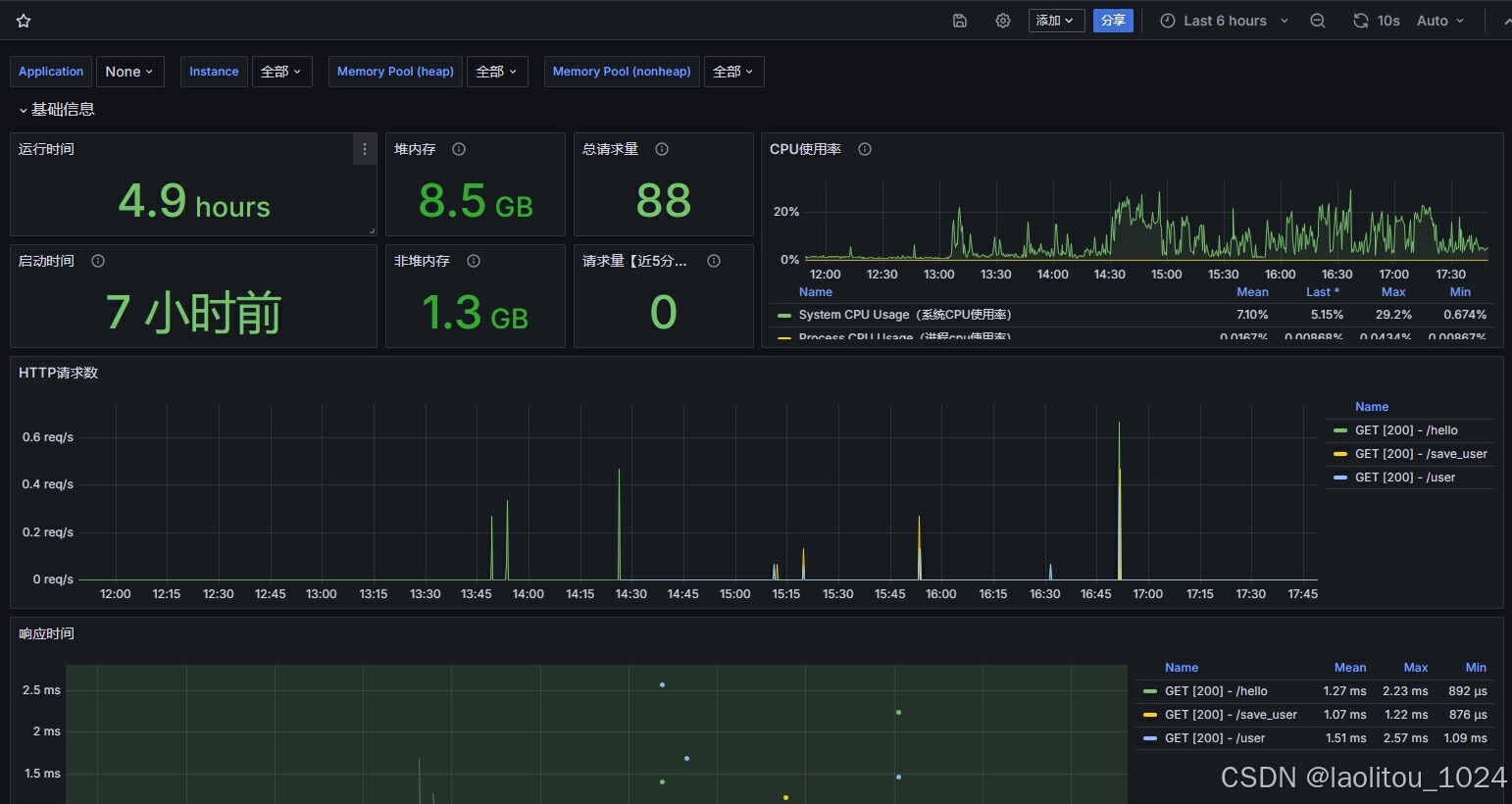
由上图中我们可以看出,BFS的遍历为四周扩散,用我们学长的话说就是周围每个点都尝试一下,无脑走,直到找到终点。由此我们可以看出来,BFS这种无脑走必定会导致时间复杂度非常高,如果终点离起点非常远,那么几乎每个点都要遍历一下,这样的话BFS这种算法就不适合了,BFS适合于点少的图,求最短距离之类的。BFS一般通过队列来实现。
下面我们将以5*5的网格,考虑{上、右上、右、右下、下、左下、左、左上}八个方向,遍历顺序为{上、右上、右、右下、下、左下、左、左上}由上开始顺时针方向,顺序可按照自己的想法,顺序不一定固定,给大家模拟实现一下过程。
注:为方便表示,对于下面的叫法特此说明,起点.上表示起点上面的格子,起点.上右表示起点右上方的格子,其他方向类似,起点.上.上右表示起点的上面格子的右上方格子。
第一步:
初始起点入队,标记起点vis[起点]==true,说明起点已经被访问了,判断起点是否为终点,起点出队,很明显不是那么从起点周围按照{上、右上、右、右下、下、左下、左、左上}的顺序八个方向遍历每一个格子,将它们一一入队,并且将它们标记为已经访问过了,即vis[八个方向]=true。

第二步:
由于我们第一步按照{上、右上、右、右下、下、左下、左、左上}的顺序入队的,此时队中的顺序是起点的{上、右上、右、右下、下、左下、左、左上}方向,那么此时出队的第一个是{上}方向,我们去遍历{上}方向的八个方向,由于{上}方向的八个方向中{上、右上、左上}三个方向下标越界,其他的都已经被访问过了,不合法,直接continue忽略掉,{上}方向遍历完成,{上}方向出队。

第三步:
此时要出队的为{上右}方向,先标记{上右}方向,然后遍历{上右}方向的八个方向,我们发现只有{上右}方向的{右}方向跟{下右}方向是合法的,其他的方向要么下标越界,要么已经被访问了,那么把{上右}方向的{右}方向跟{上右}方向的{下右}方向入队,并且标记它们的vis为true。

第四步:
此时队头的为起点的{右}方向,将它出队,判断它不是终点,那么遍历它的八个方向,发现只有它的{右下}方向是合法的,其他方向都已经被标记过了。那么将vis[右下]标记为true,将它的右下方向入队。

第五步:
此时队头的为起点的{下右}方向,将它出队,判断它不是终点,那么遍历它的八个方向,发现它的{右下、下、左下}方向是合法的,其他方向都已经被标记过了。那么将vis[右下、下、左下]标记为true,并且将其入队。此时我们发现它的右下方向是终点了,已经在栈队当中,再经过八次出队,那么就是这个出队的点就是终点了,判断完成后此时BFS搜索就结束了,由于下面都是相同的出队入队步骤,下面不再详解。

算法模板:
首先我们需要一个队列来辅助BFS实现,还需要一个初始化的输入数组,还有一个标记数组。先找到BFS的起点跟终点,确定好之后,先把起点vis==true,把起点入队,然后进入BFS函数,进入BFS函数一般先是一个大while循环,来管理队列的入队、出队。由于点都是二维的,我们一般都是用pair或者结构体来表示点,新建一个点来存储队头的信息,存完就可以让队头出队了。然后判断是否到达了目标结点,一个if判断,下面就是跟dfs一样,一个for循环遍历周围所有的点,不合法的直接continue掉,合法的标记完vis后入队,有的题目会有回溯,像在部分最短路搜索。
queue<node> q;
void bfs(){
while(!q.empty()){
node tmp=q.top();//node为(x,y)结构体
q.pop();//出队
if(到达目标终点){
更新
return;
}
//有的会有剪枝
for(int i=0;i<m;i++){//m个方向
int dx=tmp.x+bx[i];
int dy=tmp.y+by[i];
if(下标越界){
continue;
}
if(已经被标记过了){
continue;
}
//否则就是合法的
vis[dx][dy]=1;//先标记
q.push(node{dx,dy});//再新点入队
}
}
}算法例题:
现在各大算法刷题网站上bfs题目非常的多,bfs题目的变化也比较多,现在各种各样的题目层出不穷,bfs考察的还是主要分为图的遍历问题、最短路问题、连通块搜索等,下面博主选取几个比较具有代表性的给大家讲解一下,加深理解一下bfs算法。
一、图的遍历问题
迷宫问题
【题目描述】
一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由n×n的格点组成,每个格点只有2种状态,.和#,前者表示可以通行后者表示不能通行。同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点A走到点B,问在不走出迷官的情况下能不能办到。如果起点或者终点有一个不能通行(为#),则看成无法办到。
【输入】
第1行是测试数据的组数k,后面跟着k组输入。每组测试数据的第1行是一个正整数n(1≤n≤ 100),表示迷宫的规模是n×n的。接下来是一个n×n的矩阵,矩阵中的元素为.或者#。再接下来一行是4个整数ha,la,hb,lb,描述A处在第ha行,第la列,B处在第hb行,第lb列。注意到ha,la,hb,lb全部是从0开始计数的。
【输出】
k行,每行对应一个输出,如果能到达则输出"YES",否则输出"NO"。
【样例】
2
3
.##
..#
#..
0 0 2 2
5
.....
###.#
..#..
###..
...#.
0 0 4 0
YES
NO解题思路:
这类问题属于图的遍历问题,属于BFS题里面最简单的问题,直接利用BFS的思想遍历即可,判断是否能到达。之所以选这个题,是先让刚入门的小萌新熟悉一下BFS的步骤、思想。大佬可跳过此题。
AC代码:
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int n,t;
char ch[105][105];
bool flag=false,vis[105][105];
int sx,sy,fx,fy;
int bx[]={0,0,1,-1},by[]={1,-1,0,0};//方向数组
struct node{
int x,y;
};
queue<node> q;//队列
void bfs(){
while(!q.empty()){
node tmp=q.front();//取队头元素
q.pop();//出队
if(tmp.x==fx&&tmp.y==fy){//目标状态
flag=true;
return;
}
for(int i=0;i<4;i++){//周围四个方向搜索
int dx=tmp.x+bx[i],dy=tmp.y+by[i];
if(dx<0||dx>=n||dy<0||dy>=n){//下标越界
continue;
}
if(vis[dx][dy]){//已经被访问过
continue;
}
if(ch[dx][dy]=='#'){//墙壁
continue;
}
vis[dx][dy]=1;//先标记
q.push(node{dx,dy});//再入队
}
}
}
int main(){
cin>>t;
while(t--){
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>ch[i][j];
}
}
cin>>sx>>sy>>fx>>fy;
flag=false;
memset(vis,0,sizeof(vis));
while(!q.empty()){//多次输入,防止上次队列的影响
q.pop();
}
vis[sx][sy]=1;
q.push(node{sx,sy});//起点入队
bfs();
cout<<(flag?"YES":"NO")<<endl;
}
return 0;
}二、最短路问题
AcWing 1102. 移动骑士
给定一个 n∗n 的棋盘,以及一个开始位置和终点位置。
棋盘的横纵坐标范围都是 0∼n−1。
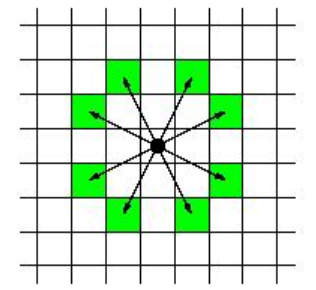
将一个国际象棋中的骑士放置在开始位置上,请问将它移动至终点位置至少需要走多少步。
一个骑士在棋盘上可行的移动方式如下图所示:
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组测试数据第一行包含整数 n,表示棋盘大小。
第二行包含两个整数 x,y 用来表示骑士的开始位置坐标 (x,y)。
第三行包含两个整数 x,y 用来表示骑士的终点位置坐标 (x,y)。
输出格式
每组数据输出一个整数,表示骑士所需移动的最少步数,每个结果占一行。
数据范围
4≤n≤300
0≤x,y≤n−1
输入样例:
3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1
输出样例:
5
28
0解题思路:
这道题跟马走日那一题几乎是一样的,但是不一样的是这道题是求的最小步数。这就是最短路问题了。还是跟之前的BFS步骤一样,就是在目标状态那里多了一个更新最小步数。这道题比前面的图的遍历问题难一点点,注意,BFS是不需要回溯的,否则会陷入死循环。
AC代码:
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
int t,n;
int sx,sy,fx,fy;//(sx,sy)起点,(fx,fy)终点
struct node{//点结构体
int x;
int y;
int dep;//步数
}Node;
int dx[]={1,1,2,2,-1,-1,-2,-2};//方向数组
int dy[]={2,-2,1,-1,2,-2,1,-1};
bool vis[305][305];//标记数组
int sum=0x3f3f3f;//最小步数
queue<node> q;
void bfs(){
while(!q.empty()){
auto tmp=q.front();
q.pop();
if(tmp.x==fx&&tmp.y==fy){//目标状态更新最小步数
sum=min(sum,tmp.dep);
return;
}
for(int i=0;i<8;i++){//八个方向遍历
Node.x=tmp.x+dx[i];
Node.y=tmp.y+dy[i];
if(Node.x<0||Node.y<0||Node.x>=n||Node.y>=n){//下标越界
continue;
}
if(vis[Node.x][Node.y]==1){//已经被访问过
continue;
}
Node.dep=tmp.dep+1;//步数更新
vis[Node.x][Node.y]=1;//先标记
q.push(Node);//再入队
}
}
}
int main(){
cin>>t;
while(t--){
memset(vis,false,sizeof(vis));//多组输入置0
sum=0x3f3f3f;//初始最大值
cin>>n>>sx>>sy>>fx>>fy;
vis[sx][sy]=1;//先标记起点
while(!q.empty()){//清空队列
q.pop();
}
q.push(node{sx,sy,0});//起点步数为0
bfs();
cout<<sum<<endl;
}
return 0;
}洛谷 P1379 八数码难题
题目描述
在 3×3 的棋盘上,摆有八个棋子,每个棋子上标有 1 至 8 的某一数字。棋盘中留有一个空格,空格用 0 来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局(初始状态)和目标布局(为了使题目简单,设目标状态为 123804765),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
输入格式
输入初始状态,一行九个数字,空格用 0 表示。
输出格式
只有一行,该行只有一个数字,表示从初始状态到目标状态需要的最少移动次数。保证测试数据中无特殊无法到达目标状态数据。
输入
283104765
输出
4
样例解释

图中标有 0 的是空格。绿色格子是空格所在位置,橙色格子是下一步可以移动到空格的位置。如图所示,用四步可以达到目标状态。并且可以证明,不存在更优的策略。
解题思路:
这道题在博主做题的感觉来说,题目质量是非常高的,思维也非常有高度,建议大家好好学一下。八数码非常类似于中国的数独游戏。在解决此题时一个布局对应一个字符串也就是一个状态,可以理解为一个布局转换为目标布局所需要的最小步数。
下面讲解一下如何解决此题,我们发现每一个字符串就是一个状态,最短距离还需要记录步数,那么我们就想到了map键值映射,由一个字符串对应初始状态到此状态的最小步数。例如:d["123048567"]=2表示由初始状态到目标状态最小步数为2步完成。其次是‘0’字符一维下标跟二维下标位置转换的技巧,我们发现每一次都是‘0’字符(空格)与四个方向的数字进行交换,属于空格的BFS,对于一维下标可以通过除3为横坐标,模3为纵坐标(3*3棋盘),由二维转为一维坐标倒过来即可,即:3*横坐标+纵坐标。刚开始可以使用find()函数查找‘0’字符的下标,然后转化为布局中的二维坐标。每完成一步就要交换格子,交换完成就得到一种新的布局,那么我们可以用count()函数去map里面查找,如果有这种状态说明之前用更小的步数就已经到达过了,没必要更新了。如果没有这种状态,那么我们就为它赋值最小步数。最后还要还原,对于这个题来说是必要的,因为四个方向搜索都是以‘0’为基础的,for循环一次把他改变了,后面的3次循环就在它前一个状态的基础上。这样交换操作就乱了。
视频讲解: 请看B站up主董晓算法,—>>点击直达<<—,博主感觉董晓老师讲的非常好,本题思路按照董晓老师讲解来写的。大家可以去看看,下面第二张图片来自董晓老师讲解。


AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<unordered_map>
using namespace std;
int dx[]={-1,0,1,0},dy[]={0,1,0,-1};//方向数组
unordered_map<string,int> d;//考虑map键值对映射,状态映射步数
queue<string> q;//棋盘状态布局
int bfs(string strat){
string end="123804765";//目标状态
q.push(strat);//初始状态
d[strat]=0;
while(q.size()){
auto s=q.front();
q.pop();
if(s==end){//目标状态
return d[s];
}
int k=s.find('0');//下标位置转化
int x=k/3;
int y=k%3;
for(int i=0;i<4;i++){//四个方向搜索
int a=x+dx[i];
int b=y+dy[i];
if(a<0||a>=3||b<0||b>=3){//下标越界
continue;
}
int distance=d[s];//记录步数
swap(s[k],s[3*a+b]);//交换
if(!d.count(s)){//新的布局
d[s]=distance+1;
q.push(s);
}
swap(s[k],s[3*a+b]);//还原
}
}
return -1;//无法到达
}
int main(){
string strat;
for(int i=0;i<9;i++){
char ch;
cin>>ch;
strat+=ch;
}
cout<<bfs(strat)<<endl;
return 0;
}三、连通块问题
第十四届省赛大学B组(C/C++)岛屿个数
到目前为止我做过像连通块问题的题用BFS解的就这一个比较好,这一道题跟连通块有结合,博主才把它归到了连通块问题来。具体的讲解跟AC代码,请看我这一篇文章,文章单独讲解了这一道题,由于文章长度限制这里不再详解,请移步下面链接。
第十四届省赛大学B组(C/C++)岛屿个数-CSDN博客文章浏览阅读1.1k次,点赞30次,收藏14次。这不是普通的DFS/BFS搜索题,看着很像最少连通块,但是题目中又有了新的定义就是在陆地环里面(被陆地包围)也算属于此外围岛屿,那么我们就也要判定这种环岛屿,博主的思路是先BFS也可DFS找出连通块的个数(四个方向),建一个vector把连通块的起点存进去,方便去找环岛屿,只要有一个起点(或者此连通块任意一个点),此连通块的点便可通过移动一网打尽,再BFS(或者DFS)判定该岛屿是否属于这种环岛屿,不属于就结果加一,属于就不用加。对于 100% 的评测用例,1≤T≤10,1≤M,N≤50。https://blog.csdn.net/m0_73633807/article/details/137248445?spm=1001.2014.3001.5501
图形搜索算法还有一种是DFS,请看博主上一篇文章数据结构与算法——DFS(深度优先搜索)
制作不易,如果对你有所帮助请三连支持博主持续创作,感谢各位大佬的支持。