题目

给你一个 二叉搜索树 的根节点 root ，和一个由正整数组成、长度为 n 的数组 queries 。

请你找出一个长度为 n 的二维答案数组 answer ，其中 answer[i] = [min_i, max_i] ：

min_i 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值，则使用 -1 代替。
max_i 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值，则使用 -1 代替。

返回数组 answer 。

示例 1 ：

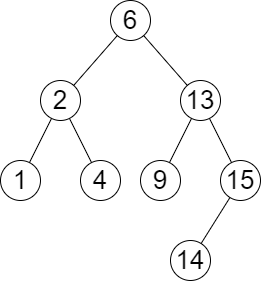
输入：root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出：[[2,2],[4,6],[15,-1]]
解释：按下面的描述找出并返回查询的答案：
- 树中小于等于 2 的最大值是 2 ，且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ，且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ，且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。

示例 2 ：

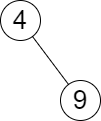
输入：root = [4,null,9], queries = [3]
输出：[[-1,4]]
解释：树中不存在小于等于 3 的最大值，且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。

提示：

树中节点的数目在范围 [2, 10⁵] 内
1 <= Node.val <= 10⁶
n == queries.length
1 <= n <= 10⁵
1 <= queries[i] <= 10⁶

关键词

二叉搜索树
二叉搜索树的中序遍历得到的内容是升序把这个内容赋给dat。所以在这里就变成了从dat种找queries[i]的answer[i]，为了加快搜索速度，可以用二分搜索。

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> dat = new ArrayList<>();
    public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
        dfs(root);
        List<List<Integer>> res = new ArrayList();
        for (int i = 0; i < queries.size(); ++i) {
            int v = queries.get(i);
            int index = binarySearch(v);
            List<Integer> r = new ArrayList();
            if (index < 0) {
                r.add(-1);
                r.add(-1);
            } else {
                if (dat.get(index) == v) {
                    r.add(v);
                    r.add(v);
                } else if (dat.get(index) < v) {
                    r.add(dat.get(index));
                    r.add(-1);
                } else if (dat.get(index) > v){
                    int k = index - 1;
                    if (k >= 0) {
                        r.add(dat.get(k));
                    } else {
                        r.add(-1);
                    }

                    r.add(dat.get(index));
                }

            }
            res.add(r);
        }
        return res;
    }
    
    private int binarySearch(int val) {
        int l = 0, r = dat.size() - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (dat.get(mid) >= val) r = mid;
            else l = mid + 1;
        }
        return r;
    }
    
    private void dfs(TreeNode root) {
        if (root == null) return;
        dfs(root.left);
        dat.add(root.val);
        dfs(root.right);
    }
}