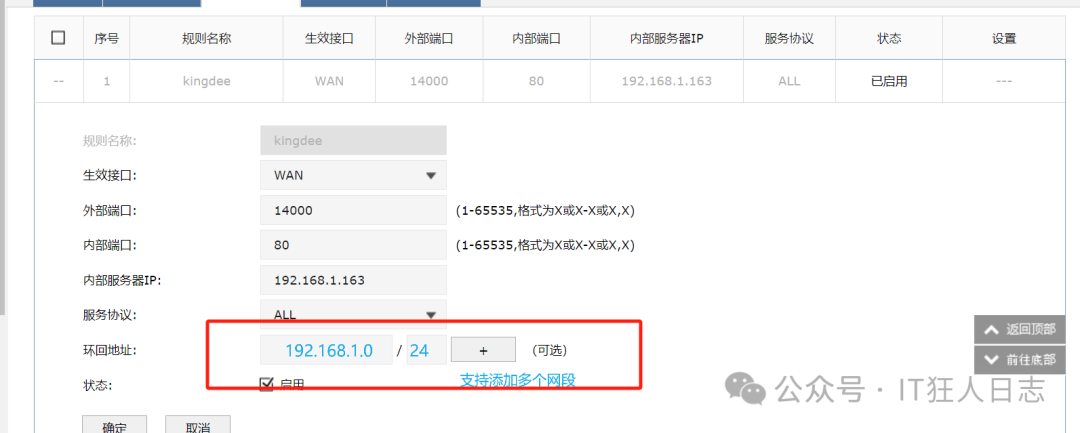
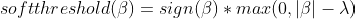1、设计表保存通话记录信息，实现相关查询功能

创建ua50tel表，并插入数据（实训报告中‘：’存在于表中但会识别为语法所以在此不使用）

依次重复上面的过程按实际输入，并查看表的内容

查询某人当月通话记录

查询某人自定义时间通话记录

查询某人和某人当月通话记录

1. 设计表保存公司组织结构信息，实现相关功能

创建表，输入数据

重复执行上述代码，按表输入的到如下表内容

查询指定部门的所有子部门信息

查询指定级别的所有部门信息

最低级别部门信息的删除

删除部门之前需要查询该部门的父部门，并将父部门的子部门中的该部门信息删除，

（这里数据输错了sub应为307，308。后面懒的改了）

删除rowkey为2-203以及sub为305的数据

再次查看发现数据少了个结果

再将该部门的相关信息进行删除