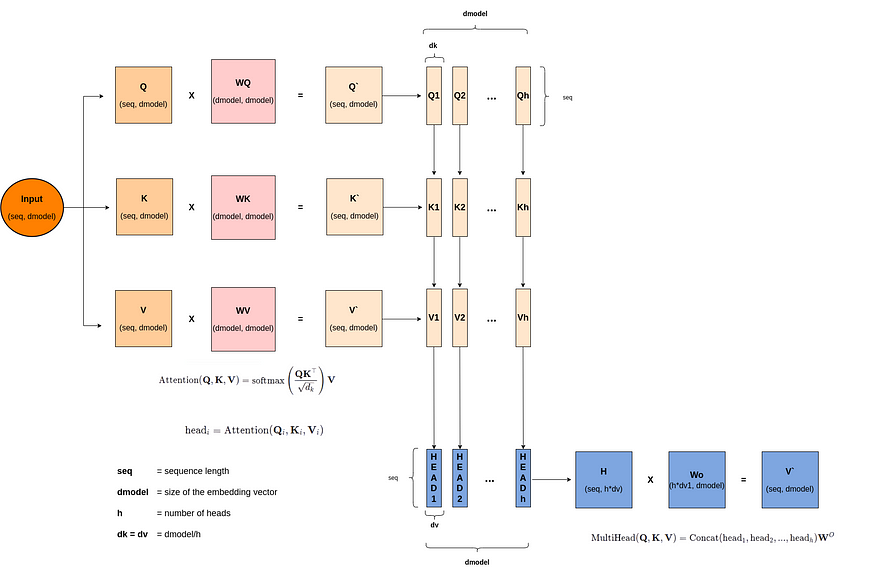
逐步对 Linear、Ridge 和 Lasso 回归进行数学理解。

LASSO(左)和岭回归(右)的约束区域
一、说明
在本文中,我们将深入探讨机器学习中两种基本正则化技术的基础和应用:Ridge 回归和 Lasso 回归。这些方法在缓解过拟合方面起着至关重要的作用,从而增强了模型对新数据的泛化能力。
二. 线性回归
线性回归是机器学习中的一种基本统计方法,它对因变量 y 和一个或多个自变量 X 之间的线性关系进行建模。在简单的回归中,我们关注一个自变量。这种关系通过公式表示:
![]()
- y 是因变量。
- X 是自变量。
- α是 Y 轴截距。
- β 是斜率(X 的系数)。
- ε 表示数据中的误差或噪声,即 y 中不能用 X 解释的部分。
2.1 成本函数
模型的拟合是使用名为 J 的均方误差 (MSE) 成本函数评估的:

- n 是数据集中的观测值数。
- ŷ(i) 是模型对第 i个观测值的预测。
- Y(i) 是第 i个观测值的 y 的实际值。
目标是最小化此函数,以找到使模型的预测尽可能接近 y 的实际值的参数α和β。
2.2 求解α和β
通过推导与 α 和 β相关的成本函数并将其设置为零,我们找到了最小化 MSE 的估计值,从而得出:
![]()
![]()
![]()
![]()
x̄ 和 ȳ bar 分别是 X 和 y 的平均值。
2.3 简单数据示例
考虑一个用于简单回归的虚构数据集:
| X | Y |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
计算β和α :
如果我们在前期方程中替换,在我们的示例 β = 2 中,为了简单起见,显示了一个没有截距的完美线性关系:y=2X
为了简化起见,我们考虑常数项 α = 0。
三、线性回归的正则化
正则化旨在通过向成本函数添加惩罚项来防止过拟合,从而降低模型的复杂性。这使我们能够获得更好地泛化到新数据的系数,但代价是训练集的准确性略有下降。
3.1 岭回归
Ridge 方法通过使用 L2 范数降低系数的复杂性来简化模型,提高了对新数据的泛化能力,即使它可能会略微降低训练集的准确性。
3.2 成本函数
单个变量的 Ridge 回归的成本函数(其中 α 是截距,β是 X 的系数)为:
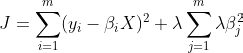
λ 是正则化超参数,β² 表示β系数的平方(在此示例中,我们考虑一个特征的单个β,α = 0)。
3.3 求解方程
为了找到最小化成本函数的 β 的值,我们计算了 J(β) 相对于 β 的偏导数,并将它们设置为零。
![]()
为简单起见,我们围绕原点进行工作,允许我们忽略 α (α=0) 并仅关注β,并为示例设置 λ=2。
将我们的值代入关于β的导数中。
我们会发现:
- 对于 λ=2 : β=1.94
- 当 λ=1 : β=1.45
- 当 λ=10 : β=1.45
- 当 λ=100 : β=0.24
在 Ridge 回归中,即使 λ 显著增加,系数 β 也永远不会正好为零。这与 L1 正则化(用于 Lasso 回归)有根本区别,L1 正则化可以将一些系数减少到零,从而执行特征选择。
从数学上讲,只要 λ 是有限的,β就永远不会完全为零。Ridge 回归中的正则化项惩罚系数的平方,这意味着无论系数是正的还是负的,其大小都会减小,而不会直接影响其符号。
四、套索回归
Lasso 回归(Least Absolute Shrinkage and Selection Operator)是一种正则化方法,它通过使用 L1 范数作为其惩罚项来区别于 Ridge 回归。这一独特功能使 Lasso 回归不仅可以通过减小系数的大小来降低模型的复杂性,还可以通过完全抵消某些系数来执行变量选择。
4.1 成本函数
Lasso 回归的成本函数(其中 α 是截距,β 是 X 的系数)由下式给出:
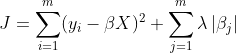
λ 是控制正则化程度的超参数。添加 λ∣β∣ 项会施加与模型系数绝对值成正比的惩罚,从而促进系数稀疏性。
4.2 计算衍生品
与 Ridge 回归不同,由于惩罚的绝对性质,Lasso 成本函数相对于 β 的导数并不那么简单。这使得求解过程复杂化,通常通过优化的数值方法求解。
4.3 求解方程
在实践中,在 Lasso 回归中寻找 α 和 β 的解决方案通常涉及优化技术,这些技术可以处理 L1 惩罚函数 β=0 时的不可微性。
可以使用子微分性原理来求解 Lasso 成本函数,因为术语 ∣β∣ 使得成本函数在 β=0 时不可微。
对于变量 X,成本函数的二次部分相对于 β 的导数(忽略 λ 惩罚,仍考虑 α=0)与线性回归模型中的导数相同。
为了纳入 L1 惩罚,使用了 ∣β∣ 的子导数,因为 ∣β∣ 在 β=0 时是不可微的。子导数 ∣β∣ 为:
- −1 如果 β<0
- 如果 β>0 为 1
- 区间 [−1,1],如果 β=0
因此,包括 L1 惩罚项在内,优化成本函数需要在更新β时考虑这些条件。
我们将使用一种直观的解决方案,即软阈值来解决问题。
4.4 简化的软阈值概念
软阈值是一种分析方法,用于调整每个系数β考虑成本函数在 β=0 时的不可微性。
简化而言,在单个系数 β 且 λ=2 的情况下,软阈值运算可以表示为:
![]()
此调整将 β 的幅度降低 λ 设定的阈值。如果调整后的 β 值低于此阈值,则系数设置为零,因此:
- 我们减小了系数的大小,以对抗过拟合。
- 我们通过消除不太重要的变量的系数来选择最重要的变量。
4.5 简单数据示例
为了说明使用相同数据集的套索回归:
| X | Y |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
我们寻求找到能够最小化成本函数β方法:
对于 λ=2 (并给出初始 β=2) :
更新β = 0
对于给定的 λ,精确的调整取决于误差和 λ 惩罚的总和。如果结果为负(表明 β 的贡献与 λ 相比不够显著),则将系数设置为零(特征选择)。
请注意,这种简化的解释旨在使软阈值的概念更易于理解,而无需深入研究复杂的数学细节(我们考虑单个 Beta 系数,并且我们简化了公式)。
总之,本文探讨了机器学习中的基本正则化技术:Ridge 和 Lasso 回归。这些方法通过战略性地调整系数来减少过拟合并增强模型泛化。岭回归可以减小所有系数的大小,而 Lasso 可以抵消一些系数,从而有助于识别最重要的变量。